Will man beispielsweise die Auswirkung der gerade beschriebenen Effekte oder verschiedener experimenteller Methoden untersuchen, ist es oft interessant, die Unterschiede zwischen Farben unter verschiedenen Bedingungen zu betrachten. Deshalb sollen nun verschiedene Maße für Farbdifferenzen vorgestellt werden sowie Befunde zur Unterscheidbarkeit von Farben aufgrund von Variationen in Farbton, Sättigung und Helligkeit.
Farbdifferenzen lassen sich auf verschiedene Arten bestimmen. Eine einfache und häufig praktizierte Möglichkeit besteht darin, die euklidische Distanz im Raum der xyL-Koordinaten der zu vergleichenden Farben zu berechnen. Lucassen und Walraven (1993) berechnen die durchschnittliche Streuung 
von n durch ihre xyL-Koordinaten bezeichneten Farben beispielsweise folgendermaßen:
wobei 
bwz. 
die Abweichung einer einzelnen Farbe in der x- bzw. y-Richtung von der Ausgangsfarbe bezeichnet. Unter der zuvor beschriebenen Annahme, daß der Farbwahrnehmung drei physiologische Kanäle zugrunde liegen, deren Output linear mit den Normfarbwerten der entsprechenden Farbe zusammenhängt, erscheint es jedoch sinnvoller, das Abstandsmaß zweier Farben aus deren Normfarbwerten (X,Y,Z) zu errechnen. Die euklidischen Distanz zwischen den 
-Koordinaten zweier Farben lautet:
wobei 
die Differenz der X-Koordinaten der beiden Farben bezeichnet, 
die Differenz der Y-Koordinaten und 
die Differenz der Z-Koordinaten. Dieses Vorgehen wird beispielsweise angewandt, um die Vorhersage durch ein bestimmtes Modell mit den empirisch gewonnenen Einstellungen zu vergleichen.
Die Anwendung dieser Formel ist jedoch nicht unproblematisch, weil der 
-Raum nicht längentreu ist, d.h. der Abstand zweier Farben im -Raum entspricht nicht dem wahrgenommenen Unterschied zwischen ihnen (oder anders formuliert: Gleiche Abstände im -Raum bedeuten nicht, daß der wahrgenommene Unterschied zwischen den dadurch repräsentierten Farben gleich ist). In Gleichung(8 werden aber alle Distanzen gleich gewichtet; es wird also Längentreue vorausgesetzt.
Indow (1988) zeigt, daß für geringe Unterschiede (die nicht deutlich über einem ebenmerklichem Unterschied liegen) zwischen Farben die Verwendung der folgenden Metrik, die auf Nickerson (1936) zurückgeht, unkritisch ist:
Diesem Abstandsmaß liegt eine Repräsentation der zu vergleichenden Farben i und j durch ihre Munsell-Neuwerte Buntheit C (chroma), Buntton H (hue) und Helligkeitswert V (value) zugrunde; dazu müssen diese Werte aber erst bestimmt werden, was nur bei Verwendung von Proben aus dem Munsell Book of Color problemlos gelingt.
Ein allgemeineres, auch für größere Farbunterschiede geeignetes und weit verbreitetes Maß 
(siehe z.B. Wyszecki & Stiles, 1982) für den Gesamtunterschied zweier Farben basiert auf dem CIE 1976 
-Raum, der annähernd gleichabständig aufgebaut ist:
wobei das Symbol 
den Unterschied der beiden zu vergleichenden Farben in der jeweiligen Dimension bezeichnet; die Berechnung von 
, 
und 
wurde bereits in den Gleichungen 3 bis 5 beschrieben. Diese Formel, auch als CIE-1976--Farbunterschiedsformel (color-difference formula) bezeichnet, gilt allerdings nur für bestimmte standardisierte Beobachtungsbedingungen.
Deshalb wurde diese Formel noch weiter verbessert (siehe Alman, 1993) und daraus die sogenannten CIE 
-Gleichungen (CIE, 1995) entwickelt, bei denen insbesondere die Gleichabständigkeit noch besser gewährleistet ist und verschiedene Parameter an die jeweilige Reizkonfiguration angepaßt werden können:
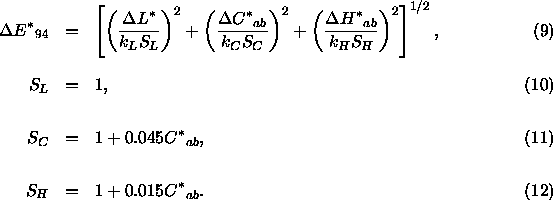
Hierbei berechnet sich 
als Differenz der beiden nach Gleichung 7 berechneten Helligkeitswerte der zu vergleichenden Farben; 
ist die Differenz der beiden Farbigkeitswerte 
, die nach Gleichung 6 berechnet wird; 
berechnet sich folgendermaßen (für kleine Farbdifferenzen)
aus den beiden Farbtonwerte 
nach Gleichung 7. Für 
kann man das geometrische Mittel der beiden -Werte einsetzen. Die Parameter 
und 
schließlich ermöglichen die Korrektur des Einflusses von Störvariablen auf den Farbunterschied, die sich aufgrund des experimentellen Aufbaus ergeben können. Dabei handelt es sich um Variablen wie Reizgröße, Struktur der Reizoberfläche oder räumliche Anordnung der zu vergleichenden Reize. Unter den Referenzbedingungen werden diese drei Werte gleich Eins gesetzt; folgende Standard-Bedingungen wurden von der CIE (1995) dazu festgesetzt:
;
Sehwinkel;
-Einheiten;
Die Unterschiedsschwelle für Farben ist abhängig von der jeweiligen Farbe; dies läßt sich auch für monochromatische Reize demonstrieren: Bietet man einer Versuchsperson in einem zweigeteiltem Feld auf der einen Seite einen monochromatischen Reiz fester Wellenlänge dar und auf der anderen Seite einen monochromatischen Reiz ähnlicher, aber variabler Wellenlänge, dann kann man ihre Unterschiedsschwelle für Wellenlängendifferenzen bestimmen. Wichtig ist bei der Durchführung derartiger Experimente, daß sich die beiden zu vergleichenden Reize nur hinsichtlich ihres Wellenlängenmaximums unterscheiden, nicht jedoch in ihrer Helligkeit (die ja - wie man am Verlauf der spektralen Hellempfindlichkeitskurve 
erkannen kann - mit der Wellenlänge ebenfalls variiert).
Eine derartige Untersuchung wird beispielsweise von Bedford und Wyszecki (1958) beschrieben: Sie überprüfen, welche Wellenlängendifferenz bei einem monochromatischen Reiz gerade noch wahrgenommen wird, wenn in einem zweigeteiltem Feld ein Standardreiz der Wellenlänge 
und ein Vergleichsreiz der Wellenlänge 
dargeboten werden. Die Autoren finden keinen systematischen Unterschied bezüglich der Richtung (ob es sich um einen Vergleichsreiz höherer oder niedrigerer Wellenlänge handelt). Sie stellen aber fest, daß die Schwelle für Farbunterschiede von der Wellenlänge des Vergleichsreizes abhängt: Es treten große Unterschiede im sichtbaren Bereich auf. In Abbildung 11 sind die Unterschiedsschwellen für den Bereich zwischen 420 und 660 nm eingezeichnet; in den Randbereichen des sichtbaren Spektrums steigt diese Unterschiedsschwelle noch deutlich an. Außerdem können Bedford und Wyszecki (1958) zeigen, daß die Unterschiedsschwellen für Reize hoher Intensität niedriger liegen und daß sie mit zunehmender Reizgröße ebenfalls abnehmen.
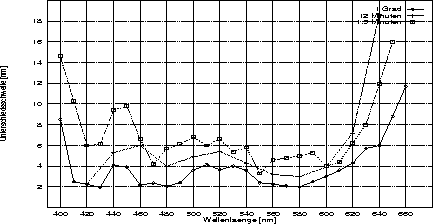
Abbildung:
Unterschiedsschwelle für Spektralfarben:
In dieser Abbildung ist die Schwelle für Farbunterschiede der Versuchsperson GW von Bedford und Wyszecki (1958) eingezeichnet; die Autoren ermitteln die Werte als arithmetisches Mittel der Unterschiedsschwelle für Vergleichsreize höherer und niedrigerer Wellenlänge. In dieser Abbildung sind die Unterschiedsschwellen für verschiedene Reizgrößen (1
, 12' und 1.5') eingezeichnet; die Werte wurden aus der Abbildung 5 von Bedford und Wyszecki (1958, S. 134) abgelesen.
Im Bereich der niedrigsten Unterschiedsschwelle bei ca. 590 nm lassen sich unter geeigneten Bedingungen monochromatische Reize, deren Wellenlängenmaximum nur 0.2 nm auseinanderliegt, unterscheiden, wie LeGrand referiert:
The minimum value ofis of the order of 1 m
by the method of limits, when the diameter of the photometric field is 2
(LeGrand, 1968, S. 284)
Auch für Unterschiede in der Sättigung von Farben zeigen sich Abhängigkeiten von der Farbe bzw. von deren bunttongleicher Wellenlänge. Um dies zu illustrieren, muß zuerst der Begriff des Sättigungsgrades (colorimetric purity) p eingeführt werden als
wobei 
die Leuchtdichte eines monochromtischen Reizes bezeichnet, der additiv gemischt mit einem neutralen Reiz der Leuchtdichte 
farbgleich ist zu der hinsichtlich des Sättigungsgrades zu beurteilenden Farbe. Die neutrale Farbe (Weiß) besitzt demnach einen Sättigungsgrad von 0, ein maximimal gesättigter (monochromatischer) Reiz einen Sättigungsgrad von 1.
Priest und Brickwedde (1938) untersuchen, welcher Sättigungsgrad zu einem ebenmerklichem Unterschied zum Weißpunkt führt: In einer Hälfte eines 4 großen quadratischen zweigeteilten Feldes wird ein weißer Standardreiz (sog. Abbot-Priest sunlight) präsentiert und in der anderen Hälfte ein Vergleichreiz, der aus einer additiven Mischung aus dem Standardreiz und einem monochromatischen Reiz der Wellenlänge in variablem Verhältnis besteht. Bei konstanter Gesamtleuchtdichte wird dann der Anteil des monochromatischen Reizes so lange erhöht, bis die Versuchsperson beim Erreichen des Wertes 
den Unterschied zum neutralen Reiz sicher wahrnehmen kann. Anschließend wird der Anteil des monochromatischen Lichts wieder so lange verringert, bis die Versuchsperson beim Erreichen des Wertes 
sicher keinen Unterschied zum neutralen Reiz mehr wahrnehmen kann. Für denjenigen Anteil p des monochromatischen Reizes, der zu einem wahrnehmbaren Unterschied führt, wird der Mittelwert aus und gebildet.
Priest und Brickwedde (1938) kommen zu dem Ergebnis (siehe Abbildung 12), daß auch die ebenmerklichen Unterschiede für den Sättigungsgrad systematisch von der Wellenlänge des verwendeten Spektralreizes abhängen: Für Reize, deren bunttongleiche Wellenlänge aus den Randbereichen des sichtbaren Spektrums stammt, liegt die Unterschiedsschwelle relativ niedrig; sie ist dagegen für aus der Mitte des sichtbaren Bereichs stammende Reize relativ hoch (ihr Maximum liegt etwa bei 570 nm).
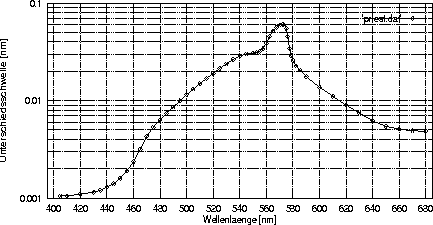
Abbildung:
Unterschiedsschwelle für den Sättigungsgrad:
In dieser Abbildung ist die Unterschiedsschwelle für den Sättigungsgrad der Versuchsperson IGP von Priest und Brickwedde (1938) zu sehen. Die zugrundeliegenden Meßwerte sind der Tabelle I von Priest und Brickwedde (1938, S. 136) entnommen.
Daß sich auch monochromatische Reize in ihrer Sättigung unterscheiden können, zeigt folgende Überlegung: Interpretiert man den Kehrwert 
des Sättigungsgrades als ein Maß für die Sättigung selbst, dann kann man folgern, daß die Sättigung im blauen Bereich des Spektrums maximal ist, ein Minimum bei Gelb hat und bei Rot wieder auf ein mittleres Niveau zunimmt. Wright und Pitt (1937) stellen ihre Befunde zur Unterschiedsschwelle beim Hinzumischen monochromatischer Strahlung zu einem Standardlicht B mit der Farbtemperatur 4800 K auf diese Weise in Form von Sättigungs-Diskriminations-Funktionen dar; Beispiele dafür sind in Abbildung 13 zu sehen.
Abbildung:
Unterschiedsschwelle für den Sättigungsgrad:
In dieser Abbildung ist die Sättigungsdiskriminationsfunktion der Versuchspersonen FHGP und WDW von Wright und Pitt (1937) zu sehen. Auf der Ordinate ist der Logarithmus der Sättigungsunterschiedsschwelle, also 
, für einen ebenmerklichen Unterschied zum Weißpunkt abgetragen. Die zugrundeliegenden Werte sind der Tabelle I von Wright und Pitt (1937, S. 331) entnommen.
Betrachtet man umgekehrt, wie viel achromatisches Licht zu einem monochromatischem Reiz bestimmter Wellenlänge hinzugemischt werden muß, damit ein sichtbarer Unterschied zu einem rein monochromatischem Reiz gleicher Wellenlänge und Leuchtdichte auftritt, so zeigt sich, daß die Unterschiedsschwelle in dieser Richtung relativ konstant ist: Für alle Wellenlängen ist ein Sättigungsgrad von 0.98 ebenmerklich von den Spektralfarben unterscheidbar (siehe Wright & Pitt, 1935).
Der von Wright und Pitt (1937) und von Priest und Brickwedde (1938) gefundene Zusammenhang zwischen Sättigung und (bunttongleicher) Wellenlänge wird auch durch die Befunde von Jones und Lowry (1926) nahegelegt: Sie bestimmen die Anzahl ebenmerklicher Unterschiede im Sättigungsgrad zwischen einem Weiß mit einer Farbtemperatur von 5200 K und acht verschiedenen Spektralreizen; die Anzahl variiert zwischen 23 Schritten bei einer Wellenlänge von 440, 640 oder 680 nm und 16 Schritten bei 575 nm. Zu ähnlichen Ergebnissen kommen auch Martin, Warburton und Morgan (1933), bei denen die minimale Anzahl an Unterscheidbarkeits-Schritten bei 570 nm liegt, während an den Enden des sichtbaren Spektrums drei mal so hohe Werte gefunden werden.
Aus den genannten Untersuchungen kann man die Folgerung ziehen, daß zwischen den Spektralfarben Unterschiede in deren Sättigung bestehen.
Besonders empfindlich ist das visuelle System für Unterschiede in der Helligkeit eines Reizes. Der gerade eben wahrnehmbare Leuchtdichteunterschied hängt vom Ausgangsniveau der Leuchtdichte ab. In Abbildung 14 ist die Empfindlichkeit für Leuchtdichteunterschiede in Abängigkeit vom Ausgangsniveau zu sehen, wie sie von Lowry (1931) als Mittelwert der Einstellungen von sechs Versuchspersonen, die Test- und Vergleichsreiz in einem 3 großem runden zweigeteilten Feld dargeboten bekommen, angegeben wird.
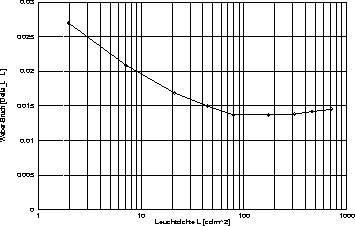
Abbildung:
Unterschiedsschwelle für Leuchtdichte:
In dieser Abbildung ist der Weber-Bruch 
für Leuchtdichteunterschiede für verschiedene Leuchtdichteniveaus zu sehen, wobei die Abszisse logaritmisch dargestellt ist. Die Daten wurden der Tabelle 1 Lowry (1931, S. 133) entnommen und wie in Anhang A beschrieben von Millilambert in 
umgerechnet.
Die minimale Unterschiedsschwelle und somit die maximale Empfindlichkeit für Leuchtdichteunterschiede liegt zwischen 80 und 300 . Bei Leuchtdichten über 100 trifft hierbei das Webersche Gesetz annähernd zu: Es besteht ein konstanter Zusammenhang zwischen dem Zuwachs an Leuchtdichte 
, der für einen wahrnehmbaren Unterschied erforderlich ist, und dem Ausgangsniveau der Leuchtdichte L; für diese Leuchtdichten liegt der Weber-Bruch bei etwa 0.01; es sind also Veränderungen der Leuchtdichte um etwa 1% wahrnehmbar.
zurück zur Hauptseite (Farbwahrnehmung)
zurück zu meiner homepage
Anmerkungen und Mitteilungen an
rainer@zwisler.de
