Diskriminationsellipsoide, deren Projektion auf die Normfarbtafel beispielsweise in Abbildung 19 zu sehen ist, veranschaulichen die Streuung der Einstellungen der Versuchsperson in einem mehrdimensionalen Raum (im Fall der Farbeinstellungen dreidimensionalen). Werden die Radien dieser Ellipsen dabei als Standardabweichung der Daten in die jeweilige Richtung bestimmt, dann können sie als Kontur eines ebenmerklichen Unterschieds interpretiert werden. Deshalb werden sie als Diskriminationsellipsen bezeichnet.
Voraussetzung für die Bestimmung der Diskriminationsellipsen ist, daß die betreffende Variablen multivariat normalverteilt ist. Nach Brown (1952a) kann davon ausgegangen werden, daß dies auf die bei Farbabgleichen erhobenen Farbörter zutrifft. Silberstein und MacAdam (1945) können beispielsweise für die Ergebnisse der Versuchsperson PGN bei dem von MacAdam (1942b) beschriebenen Experiment eine Normalverteilung der Koordinaten der Einstellungen in der Normfarbtafel nachweisen. Allerdings konnte diese Versuchsperson ihre Einstellungen nicht frei wählen, sondern nur jeweils auf einer vorgegebenen Geraden im Farbraum; diese Einschränkung gilt für den Nachweis der Normalverteilung bei Brown (1952a) nicht, da hier von den Versuchspersonen die Intensität von drei Primärfarben frei variiert werden kann. In Anbetracht dieser Befunde wird im folgenden eine multivariate Normalverteilung der Normfarbwerte der wiederholten Einstellungen der Versuchspersonen angenommen.
Die folgenden Ausführungen basieren auf Tatsuoka (1971). Die allgemeine Form der multivariaten Normalverteilung lautet im p-dimensionalen Fall für die Dichtefunktion 
eines Zufallsvektors 
wobei 
den Erwartungswertsvektor - auch Zentroid genannt - und 
die Varianz-Kovarianz-Matrix bezeichnen; es gelte also
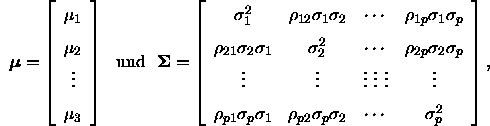
wobei 
die Varianz von 
bezeichnet und 
, den Korrelationskoeffizient zwischen und 
. 
bezeichnet die Determinante der Varianz-Kovarianz-Matrix und 
ist schließlich deren Inverse. 
bezeichnet man auch als quadratische Form 
; diese quadratische Form spezifiziert ein Ellipsoid im p-dimensionalen Raum, dessen Zentrum im Ursprung liegt.
Farben lassen sich durch Elemente eines dreidimensionalen Vektorraums repräsentieren; deshalb soll nun der Fall der dreidimensionalen Normalverteilung
genauer betrachtet werden. Hier sieht die Varianz-Kovarianz-Matrix folgendermaßen aus:
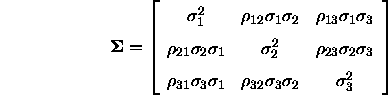
bzw. für symmetrische Matrizen (wie sie bei Farbabgleichen angenommen werden)
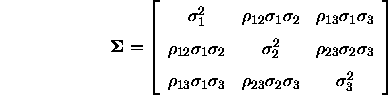
Für unsere Betrachtungen wird nun von einer symmetrischen Matrix ausgegangen. Ihre Determinante lautet dann
Verwendet man für die Varianz-Kovarianz-Matrix einer symmetrischen Matrix die einfachere Schreibweise
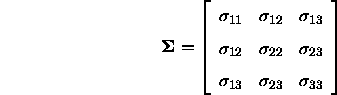
so berechnet sich ihre quadratische Form 
für einen dreidimensionalen Vektor 
relativ einfach als
Als Isodensiten bezeichnet man Konturen gleicher Wahrscheinlichkeitsdichte. Die von einer Isodensite eingeschlossene Fläche bzw. der von ihr umfaßte Raum kann als Konfidenzintervall um den Mittelwertsvektor aufgefaßt werden.
Betrachtet man nochmals die Dichtefunktion der mehrdimensionalen Normalverteilung in Gleichung 13, so sieht man, daß die Daten 
nur in der quadratischen Form im Exponenten der Dichtefunktion vorkommen. Daraus ergibt sich, daß für jede Konstante 
aus 
die Menge aller , für die gilt
auch den selben Wert von und somit auch die selbe Wahrscheinlichkeitsdichte besitzt. Bei der aus Gleichung 14 resultierenden Kontur gleicher Wahrscheinlichkeitsdichte handelt es sich somit um eine Isodensite im oben beschriebenen Sinne. Der zu diesem Konfidenzintervall gehörende Wahrscheinlichkeitswert hängt dabei monoton von C ab.
Die Bestimmung des absoluten Wahrscheinlichkeitsniveaus basiert auf folgendem Theorem von Tatsuoka (1971):
Die Wahrscheinlichkeit dafür, einen Wert zu erhalten, der innerhalb des Ellipsoids (bzw. Konfidenzbereichs) liegt, ist nach diesem Theorem gleich der Wahrscheinlichkeit dafür, daß eine 
-Größe mit p Freiheitsgraden nicht den für 
gewählten Wert überschreitet.
Dieses Theorem darf allerdings nur bei gegebener Dichtefunktion angewendet werden; dazu muß insbesondere die Varianz-Kovarianz-Matrix schon gegeben sein und darf nicht aus den Daten geschätzt werden. In der Praxis muß man jedoch oft einen Schätzer 
dafür verwenden, der sich folgendermaßen berechnet:
Man erhält im Fall von aus den Daten zu schätzender Varianz-Kovarianz-Matrix nach Fahrmeir und Hamerle (1996) die sogenannte Mahalanobis-Distanz
mittels derer man den 
-Vertrauensbereich um eine p-variate normalverteilte Zufallsvariable durch
bestimmen kann. Die Mahalanobis-Distanz entspricht der in den vorangehenden Ausführungen verwendeten Konstante C; dadurch wird also wieder ein Ellipsoid mit Mittelpunkt 
definiert.
Will man im mehrdimensionalen Fall die Isodensiten der Normalverteilung mit der quadratischen Form 
berechnen, so lassen sich die Eigenwerte und Eigenvektoren der Varianz-Kovarianz-Matrix dazu verwenden.
Die Bestimmung der Eigenwerte und Eigenvektoren kann folgendermaßen geschehen: Zuerst werden die Eigenwerte der Matrix bestimmt: Aus der oben dargestellten Gleichung(16 folgt
und somit
Daraus erhält man nur dann eine nichttriviale Lösung, wenn die Koeffizientenmatrix 
gleich Null ist; deshalb muß auch deren Determinante Null sein:
Sind nun die Eigenwerte bekannt, kann man auch die Eigenvektoren berechnen, indem jeder einzelne Eigenwert 
in die Gleichung(17 eingesetzt wird. Dabei kann jeweils ein Element des Eigenvektors frei gewählt werden. Sollen die Eigenvektoren normiert werden, können sie mit einer entsprechenden Proportionalitätskonstante multipliziert werden. Oft werden die Eigenvektoren auch auf die Länge Eins normiert, indem man sie mit ihrer Norm 
multipliziert.
Kennt man nun die Eigenwerte und Eigenvektoren der Varianz-Kovarianz-Matrix, kann man auch die elliptischen Isodensiten bestimmen: Die Eigenvektoren einer symmetrischen Matrix - dies ist bei der Varianz-Kovarianz-Matrix der Fall - stehen senkrecht aufeinander und bestimmen die Orientierung der Hauptachsen der Ellipse; die Längenverhältnisse der Hauptachsen a und b der elliptischen Isodensiten sind durch die Quadratwurzeln der zugehörigen Eigenwerte gegeben. Nun lassen sich die zweidimensionalen Isodensiten durch folgende Formel berechnen:
Zu jedem Koordinatenvektor , für den die quadratische Form den Wert C annimmt (er liegt also auf der durch C festgelegten Isodensite), existiert ein Winkel 
, für den diese Gleichung gilt. Läßt man nun nacheinander Werte zwischen 0 und 
annehmen, erhält man die einzelnen Punkte der Isodensite.
Zur praktischen Bestimmung der Diskriminationsellipsoide muß man also zuerst die dreidimensionale Varianz-Kovarianz-Matrix für die bei einem Zielreiz gemessenen Einstellungen berechnen. Aus dieser werden dann die Eigenwerte und Eigenvektoren bestimmt. Man wählt dann das 
-Niveau, so daß Prozent der Fälle innerhalb der Ellipse zu liegen kommen, und bestimmt daraus zusammen mit dem Stichprobenumfang und der Tatsache, daß es sich um einen dreidimensionalen Raum handelt, die Schwelle C. Schließlich erfolgt zur grafischen Darstellung jeweils eine Projektion des dreidimensionalen 
-Raumes auf die 
-Ebene, die 
-Ebene und die 
-Ebene.
Sehr bekannt sind die von MacAdam (1942b) bestimmten Diskriminationsellipsen. Sie kommen auf ganz andere Art als gerade beschrieben zustande; folgendes Experiment ist zu ihrer Bestimmung erforderlich: Den Versuchspersonen (bei MacAdam (1942) waren es zwei) wird vor einem gleichmäßig ausgeleuchtetem neutralen Hintergrundfeld von etwa 42
Sehwinkel ein zweigeteiltes Reizfeld von 2 Sehwinkel dargeboten, bei dem auf einer Seite ein Standardreiz vorgegeben ist, auf der anderen Seite ein Vergleichsreiz, dessen Farbton sich bei konstant gehaltener Leuchtdichte verändern läßt: Die Versuchsperson kannt durch Betätigen eines Drehreglers das Mischungsverhältnis zweier annähernd monochromatischer Lichtstrahlen verändern. Die beiden für diese Mischung gewählten Reize sind so gewählt, daß bei einem bestimmten Mischungsverhältnis Farbgleichheit zum auf der anderen Seite vorgegebenen Standard möglich ist. Diese Prozedur wird 50 mal wiederholt, um die Standardabweichung der Einstellungen der Versuchsperson bestimmen zu können.
Insgesamt werden für jeden Standardreiz zwischen sechs und acht verschiedene Paare von zu mischenden Reizen vorgegeben, deren Mischung jeweils gleich dem Standard sein kann und auch von der Versuchsperson so eingestellt werden solle. Trägt man nun die für die einzelnen Reizpaare erhaltenen Standardabweichungen auf die Verbindungsgerade der Farbörter der beiden zu mischenden Reize in der Normfarbtafel ein, so beschreiben diese zusammen eine Ellipse, die angibt, ab welchen Differenzen Farben unterschieden werden können (bei konstanter vorgegebener Leuchtdichte). Da bivariat normalverteilte Daten angenommen werden, beträgt die Wahrscheinlichkeit dafür, daß ein Datenpunkt in eine aus den Standardabweichungen bestimmte Ellipse fällt, etwa 39%, wie bei Howe, Jackson und Morris (1956) begründet wird.
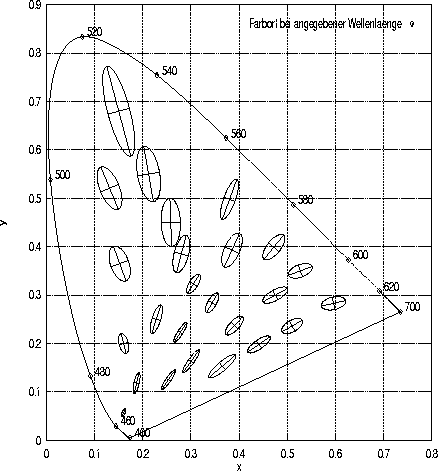
Abbildung 15:
Diskriminationsellipsoide nach MacAdam (1942b):
In dieser Abbildung sind 25 der von MacAdam (1942b) bei seiner Versuchsperson PNG erhobenen Diskriminationsellipsen (in zehnfacher Vergrößerung) sowie deren Hauptachsen zu sehen. Die von der Versuchsperson einzustellenden Reize werden monokular mit fest vorgegebener Leuchtdichte präsentiert. Für die Zeichnung wurden die von Wyszecki und Stiles aus den Grafiken von MacAdam (1942b) Beobachtungen abgelesenen und in Tabelle 2(5.4.1.) (Wyszecki & Stiles, 1982, S. 309) aufgeführten Werte verwendet.
Werden diese Ellipsen nun für verschiedene Farbörter wie in Abbildung 15 dargestellt, erhält man eine Übersicht darüber, wie sich die Unterscheidbarkeit von Farben in verschiedenen Regionen der Normfarbtafel verändert. MacAdam (1942b, S. 267 f.) schreibt dazu:
Such a series of ellipses would therefore represent all the information contained in all the curves for the noticeabilities of purity and dominant wave-length change. In addition, these ellipses represent the noticeabilities of all conceivable combinations of purity and dominant wave-length differences. (MacAdam, 1942b, S. 267 f.)
Es ist zu beachten, daß diese Diskriminationsellipsen von MacAdam (1942b) zunächst für nur einen Beobachter erhoben und aufgezeichnet werden. Brown und MacAdam (1949) führen Versuche durch, in denen die Diskriminationsellipsen durch die Mischung dreier Primärfarben, die monokular vor dunklem Hintergrund in 2 Größe dargeboten wurden, bestimmt werden; dabei ist auch eine Variation der Leuchtdichte möglich. Für zwei Beobachter und 38 verschiedene Farben werden die Diskriminationsellipsen bestimmt, wobei von einer Normalverteilung der Einstellungen ausgegangen wird. Die Bestimmung der Ellipsen erfolgt hier nach der im vorigen Abschnitt beschriebenen Methode, wobei für die Schwelle C in dieser Untersuchung der Wert 1 gesetzt wird, um die Ergebnisse mit denen von MacAdam (1942b) vergleichen zu können. Die auf diese Weise für die Versuchsperson WRJB erhaltenen Diskriminationsellipsen sind in Abbildung 16 zu sehen; aufgrund der hier angenommenen trivariaten Normalverteilung beträgt die Wahrscheinlichkeit dafür, daß ein Datenpunkt in das entsprechende Ellipsoid fällt, nur etwa 20%, wie Brown et al. (1956) nachweisen, und nicht 68%, wie Brown und MacAdam (1949) fälschlicherweise behaupten.
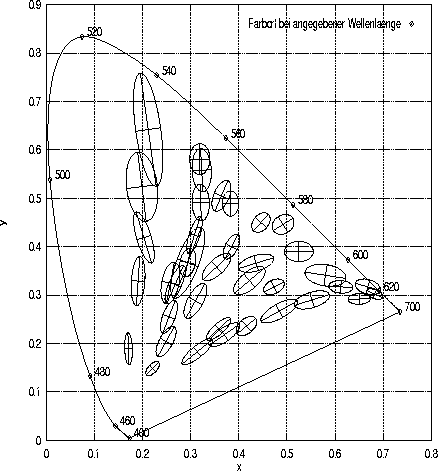
Abbildung 16:
Diskriminationsellipsoide nach Brown und MacAdam (1949):
In dieser Abbildung sind 38 der von Brown und MacAdam (1949) bei seiner Versuchsperson WRJB erhobenen Diskriminationsellipsen (in zehnfacher Vergrößerung) sowie deren Hauptachsen zu sehen. Grundlage der Darstellung sind die von Brown und MacAdam (1949, S.824 f.) in ihrer Tabelle V veröffentlichten Schätzungen der Ellipsenparameter. Die monokular präsentierten, 2 großen Reize werden von den Versuchspersonen auf allen drei Dimensionen verändert.
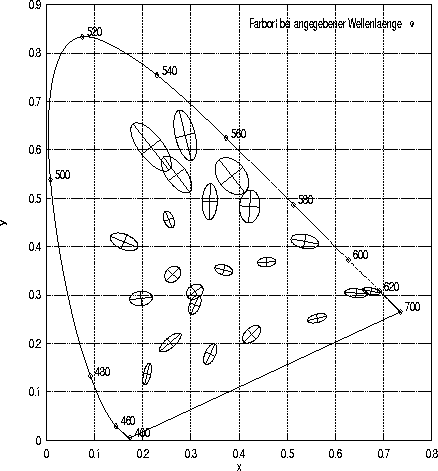
Abbildung 17:
Diskriminationsellipsoide nach Brown (1957):
In dieser Abbildung sind die 22 von Brown (1957) bei zwölf Versuchspersonen erhobenen Diskriminationsellipsen (in zehnfacher Vergrößerung) sowie deren Hauptachsen zu sehen. Grundlage der Darstellung sind die von Brown (1957, S. 139) in der Tabelle III veröffentlichten Schätzungen der nach dem dort beschriebenen Verfahren gewichteten Ellipsenparameter. Die 10 großen Reize können im Gegensatz zu den beiden vorher dargestelten Untersuchungen hier beidäugig betrachtet werden.
Brown (1957) versucht schließlich, die genannten Ergebnisse noch zu weiter generalisieren, indem er ähnliche Untersuchungen an zwölf Versuchspersonen durchführt, von denen nur der Autor selbstmit der Fragestellung vertraut ist. Bei dieser Untersuchung kann der 10 große Zielreiz beidäugig betrachtet werden. Von jedem Beobachter werden für jeden der 22 Zielreize 60 Farbabgleiche durchgeführt. Auch die Ergebnisse auf dieser breiten empirischen Basis stimmen mit den beiden zuvor genannten in bezug auf die Größe und Lage der Diskriminationsellipsen überein, wie in Abbildung 17 zu sehen ist.
Brown's (1957) untersucht, wovon die Größe der Diskriminationsellipsen außer dem Farbort noch abhängt. Die Versuchspersonen sind zu Beginn des Experiments nicht im Herstellen von Farbgleichheiten mit der verwendeten Apparatur vertraut. Vor Beginn des eigentlichen Experiments erfolgt deshalb eine knapp einstündige Übungssitzung, in der ein annähernd neutraler Reiz eingestellt werden soll. Dann werden in 22 Sitzungen jeweils 60 Abgleiche zu einem für die Dauer dieser Sitzung festen Standardreiz eingestellt. Brown (1957) vergleicht die in Abbildung 18 gezeigten Diskriminationsellipsen aller zwölf Beobachter aus der ersten experimentellen Sitzung mit denen aus der siebzehnten experimentellen Sitzung zum Nachweis eventueller Übungseffekte.
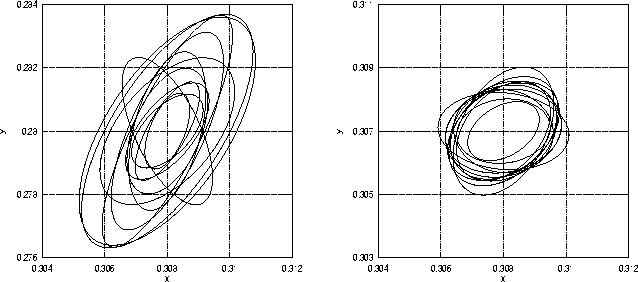
Abbildung:
Übungseffekte bei Brown (1957): Hier sind die Ergebnisse der zwölf Versuchspersonen von Brown (1957) zu sehen. Im linken Teil sind die Diskriminationsellipse für den erste im Experiment dargebotenen Standardreiz gezeigt, im rechten Teil für den siebzehnten. Es zeigen sich deutlich die im Text näher beschriebenen Übungseffekte. Die Parameter der Ellipsen wurden für die linke Abbildung aus der Tabelle IV und für die rechte Abbildung aus der Tabelle V von Brown (1957) entnommen
Dabei zeigt sich, daß sich die Ellipsen aus der ersten Sitzung zwischen den Versuchspersonen deutlich in ihrer Größe und Orientierung unterscheiden; in der siebzehnten Sitzung ist dies nicht mehr der Fall. Brown (1957) interpretiert dieses Ergebnis so, ``that all of the observers by the time they had matched the seventeenth color center could be considered skilled observers'' (Brown, 1957, S.140). Dieses Ergebnis läßt sich aber auch so deuten, daß mit zunehmender Übung die Einstellungen der Versuchspersonen konsistenter werden, also individuelle Unterschiede mit zunehmender Übung in den Hintergrund treten.
Neben der größeren Übereinstimmung zwischen den Ellipsen fällt außerdem auf, daß die durchschnittliche Größe der Ellipsen deutlich abnimmt; dies scheint kein alleiniger Effekt des unterschiedlichen Farbortes der beiden Standarreize zu sein, da beide in der Normfarbtafel relativ nahe beieinander liegen und es sich zudem um einen Bereich handelt, in dem die Größe der Diskriminationsellipsen keinen großen systematischen Schwankungen unterliegt, wie in den Abbildungen 15 und 16 zu sehen ist.
Brown (1952b) untersucht, aufgrund welcher Besonderheiten des Versuchsaufbaus sich die Unterscheidbarkeit von Farben und damit die Größe der jeweiligen Diskriminationsellipsen verändert. Er verändert die Größe, in der die von der Versuchsperson abzugleichenden Reize präsentiert werden, zwischen 2 und 12 Sehwinkel. Außerdem werden diese Reize vor einem unterschiedlich beleuchtetem Hintergrund dargeboten. Um den Einfluß dieser Variationen auf das Diskriminationsvermögen der Versuchsperson zu bestimmen, untersucht Brown (1952b) die Streuungen der Farbabgleiche der Versuchsperson und berechnet daraus nach dem in Brown und MacAdam (1949) beschriebenen Verfahren Diskriminationsellipsen. In Abbildung 19 ist zu sehen, wie sich die genannten Faktoren auf die Einstellungen der Versuchsperson WRJB bei einem roten Zielreiz auswirken.
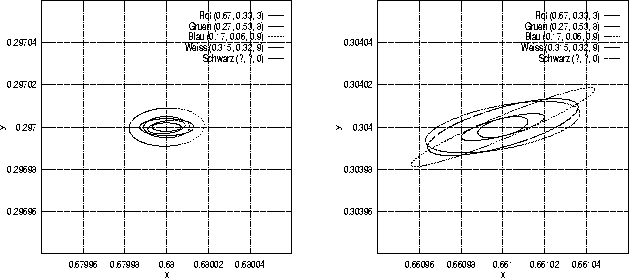
Abbildung 19:
Diskriminationsellipsoide nach Brown (1952b): Hier sind die Ergebnisse von Brown (1952b) für die Versuchsperson WRJB bei dem roten Standardreiz in einem Ausschnitt der Normfarbtafel dargestellt: Im linken Teil sind die Diskriminationsellipsen für den 12 großen roten Reiz mit den xyY-Koordinaten (0.680, 0.297, 4.7) vor den verschiedenfarbigen Hintergründen angegeben, im rechten Teil sind die Ellipsen für den 2 großen roten Reiz mit den xyY-Koordinaten (0.661, 0.304, 4.7) zu sehen. Der Y-Wert ist in Fuß-Lambert angegeben. Die in den Abbildungen angegebenen Koordinaten der Hintergrundreize wurden aus der Abbildung 1 von Brown (1952b, S.838) abgelesen; die Ellipsenparameter stammen aus Tabelle III von Brown (1952b, S. 840).
Für diesen wie für die anderen von Brown (1952b) verwendeten Reize ergibt sich eine ähnliche Systematik in den Befunden, die insbesondere bei einem grünen Reiz noch stärker ausgeprägt ist: Die Diskriminationsleistung der Versuchsperson ist am höchsten, wenn der Reiz vor einem Hintergrund dargeboten wird, dessen Farbe dem Reiz selbst ähnlich ist. Eine Vergrößerung des Reizes von 2 auf 12 bringt außerdem für alle Hintergrundvarianten eine deutliche Verbesserung der Diskriminiationsfähigkeit. In diesem Fall wirken sich auch andersfarbige Hintergrundbeleuchtungen nicht so stark aus wie bei kleineren Zielreizen.
zurück zur Hauptseite (Farbwahrnehmung)
zurück zu meiner homepage
Anmerkungen und Mitteilungen an
rainer@zwisler.de
