Nach der Beschreibung wichtiger Phänomene der Farbwahrnehmung im vorherigen Abschnitt sollen nun verschiedene Modelle zu deren Erklärung genannt werden. Wyszecki und Stiles (1982) unterteilen die Theorien zur Farbwahrnehmung in drei Klassen: In diesem Abschnitt sollen die auf den Absorptionsspektren der Rezeptortypen aufbauende Theorien, die neuronalen Theorien, die über die Rezeptorebene hinausgehen, und die Linienelement-Theorien jeweils kurz dargestellt werden.
Die sogenannten Rezeptorkurven-Theorien gehen von den verschiedenen Rezeptortypen auf der Retina aus, die sich in ihrem zu Beginn dieser Arbeit beschriebenen Absorptionsspektrum unterscheiden. Der Absorption liegt das Prinzip der Univarianz zugrunde (Rushton, 1972; Kaiser & Boynton, 1996), das besagt, daß zwei beliebige Lichtreize, die vom Sehfarbstoff Rhodopsin gleich absorbiert werden, auch zu einer gleichen Reaktion der Zapfen führen. Die für jeden Zapfentyp charakteristische spektrale Empfindlichkeit beschreibt die Wahrscheinlichkeit, mit der ein Photon absorbiert wird, als Funktion der Wellenlänge (siehe Abbildung 1.1). Die aus der Absorption resultierende Zapfenerregung hängt nur von der Anzahl absorbierter Photonen ab, nicht von deren Wellenlänge, da die Wellenlängeninformation verloren geht, sobald ein Photon erst einmal absorbiert worden ist. Aus dem Prinzip der Univarianz folgt, daß die spektralen Hellempfindlichkeitskurven der Zapfentypen linear mit den relativen Absorptionsspektren der drei Farbrezeptor-Arten zusammenhängen müssen (siehe Wyszecki & Stiles, 1982, S. 587). Diese spektralen Empfindlichkeiten nennt man auch König-Fundamentals nach A. König, von dem die ersten empirisch ermittelten Kurven dieser Art stammen.
Diese König-Fundamentals stimmen gut mit den spektralen Empfindlichkeiten der 
-Mechanismen
von Stiles (1959) überein und auch die von Baylor et al. (1987) und Schnapf et al. (1987) berichteten Absorptionsspektren der verschiedenen Pigmente der Zapfentypen sind ebenfalls sehr ähnlich. Verschiedenste Arten, diese fundamentalen Empfindlichkeitsfunktionen der Zapfen zu bestimmen, führen also zu sehr ähnlichen Ergebnissen, deren geringfügige Unterschiede von Wyszecki und Stiles (1982, S. 633) diskutiert werden. Das Besondere an dieser Übereinstimmung ist, daß die Daten auf völlig verschiedene Weise zustande kommen: Die König-Fundamentals basieren auf Farbwertkurven und Verwechslungslinien, also letztlich auf Farbabgleichen, die Empfindlichkeiten der -Mechanismen werden aus Schwellen für wahrnehmbare Inkremente abgeleitet und die Absorptionskurven der Sehpigmente werden durch physiologische Messungen bestimmt. Diese drei unterschiedlichen Herangehensweisen belegen alle, daß drei Mechanismen mit einer bestimmten Charakteristik die Grundlage des Farbensehens bilden.
Rushton (1972) schlägt ein Modell der Farbwahrnehmung vor, das direkt auf den Reaktionen der Rezeptortypen basiert und das Farbadaptation dadurch erklärt, daß die Pigmente der Rezeptoren bei Absorption von Licht bleichen, d.h. in einen anderen chemischen Zustand zerfallen, wodurch sich die Empfindlichkeit der Zapfensysteme verändert (siehe auch Kaiser & Boynton, 1996). Dabei herrscht ein chemisches Gleichgewicht zwischen der gebleichten und der ungebleichten Form des Sehpigments, das mit zunehmender Absorption von Photonen in Richtung gebleichter Pigmente verschoben wird. Dadurch wird eine verstärkte Neigung zum Wiederherstellen der gebleichten Moleküle ausgelöst.
MacLeod und Boynton (1979) stellen einen dreidimensionalen Farbraum vor, der direkt auf physiologischen Messungen aufbaut und dessen Achsen durch die Erregung der drei Rezeptortypen L, M und S gegeben sind. Sie gehen von der Annahme aus, daß die Rezeptoren des S-Systems nicht zur Gesamt-Leuchtdichte beitragen und daß die Summe der Erregungen von L und M konstant sei und damit gleich Eins gesetzt werden kann. Dann lassen sich die Koordinaten einer Farbe in diesem Raum folgendermaßen repräsentieren:
MacLeod und Boynton (1979) nennen als Vorteile dieser Darstellungsweise, daß die Erregung der einzelnen Rezeptorsysteme direkt repräsentiert ist und daß gleichen Entfernungen auf einer Linie in dieser Farbtafel auch gleiche Veränderungen der Rezeptorerregungen für die drei Zapfenarten entsprechen. Dieser Farbraum dient als Grundlage für den in Abschnitt 1.2.3 beschriebenen DKL-Farbraum.
Das farbliche Aussehen eines Reizes wird nicht nur von der Erregung der drei Rezeptorarten bestimmt, sondern auch durch eine Weiterverarbeitung der Rezeptorsignale auf höherer neuronaler Ebene, wie unter anderem von Jameson und Hurvich (1964) oder Shevell (1978, 1982) belegt wird. Alle derartigen Modelle, die sogenannten Gegenfarben-Theorien, gehen dabei von antagonistischen Farbmechanismen auf dieser höheren Ebene aus. Hering (1920) postuliert beispielsweise drei antagonistische Prozesse als Grundlage des Farbensehens, nämlich einen Rot-Grün-Prozeß, einen Gelb-Blau-Prozeß und einen Weiß-Schwarz-Prozeß, wobei keine Farbe gleichzeitig beide Farbtöne des jeweiligen Antagonisten-Paares annehmen kann.
Jameson und Hurvich (1955) quantifizieren dieses Modell durch Anwendung der Farbaufhebungs-Methode (color cancellation method), bei der das Mischungsverhältnis von zwei Farbreizen so eingestellt werden soll, daß deren Mischung weder rötlich noch grünlich (bzw. weder bläulich noch gelblich) erscheint. Der Rotanteil eines Reizes läßt sich dann dadurch bestimmen, wieviel Grün hinzugemischt werden muß, um eine weder rötliche noch grünliche Mischung zu erhalten. Die Erregung des Rot-Grün-Mechanismus durch einen Spektralreiz der Wellenlänge 
läßt sich durch die Differenz zwischen der Intensität des roten Anteils und des grünen Anteils 
beschreiben; ähnlich verhält es sich mit der Intensitätsdifferenz 
des Gelb-Blau-Systems. Durch Variieren der Wellenlänge lassen sich so die spektralen Reaktionskurven der Gegenfarben-Systeme empirisch bestimmen. Hurvich und Jameson (1955, S.602) geben aber auch an, wie diese Reaktionskurven als Linearkombination der CIE-1931-Spektralwertkurven berechnet werden können (empirische Befunde, die gegen diese Linearitätsannahme sprechen, werden im nächsten Abschnitt besprochen). Jameson & Hurvich (1956) beschreiben, wie auch Kontexte und neutrale Reize im Rahmen dieser Theorie berücksichtigt werden können.
Die von Jameson und Hurvich (1955, 1956) und Hurvich und Jameson (1955) dargestellte Gegenfarben-Theorie dient zur Beschreibung der Ergebnisse von Farbaufhebungs-Experimenten, die formalen Voraussetzungen für eine Gegenfarben-Theorie werden aber von diesen Autoren nicht betrachtet. Von Krantz (1975b) wird dazu die Gegenfarben-Theorie axiomatisiert, indem die aus Abschnitt 1.1.2 bekannte Graßmann-Struktur 
um die Teilmengen 
(Rot-Grün-Äquilibria) und 
(Gelb-Blau-Äquilibria), zu einer Gegenfarben-Struktur 
erweitert wird. Sind neben den für eine trichromatische Graßmann-Struktur notwendigen Axiomen noch drei Axiome empirisch erfüllt, die die Linearität der Gegenfarben-Attribute sicherstellen, dann gilt der folgende Repräsentationssatz (Theorem 6 bei Krantz, 1975b):
Dies bedeutet, daß die Funktionen 
und 
eindeutig sind bis auf Maßstabsänderungen und Vorzeichenwechsel.
Krantz (1975b) zeigt außerdem, daß auch dann ein linearer Farbcode auf der Graßmann-Struktur konstruiert werden kann, wenn das Axiom der Linearität nur von einer einzigen Äquilibriums-Menge erfüllt wird. Dies ist aus empirischen Gründen von großer Bedeutung, denn Larimer, Krantz und Cicerone (1974) können zwar für die Rot-Grün-Koeffizienten keine Verletzung der Linearität nachweisen, aber für die Gelb-Blau-Koeffizienten weisen Larimer, Krantz und Cicerone (1975) deutliche Abweichungen von der Linearität nach. Ikeda und Ayama (1980) können unter Anwendung der oben beschriebenen Farbaufhebungs-Methode Hinweise darauf finden, daß die Gelbempfindung aus einer nichtlinearen Kombination zweier Zapfenreaktionen resultiert. Mausfeld (1998) greift die Axiomatisierung der Gegenfarben-Theorie von Krantz (1975b) auf und nennt weitere empirische Belege für Verletzungen der geforderten Axiome.
Trotz dieser Verletzungen der Linearität soll nun ein auf Gegenfarben aufbauender Farbraum dargestellt werden, der eine anschauliche Repräsentation von Innenfeld-Umfeld-Konfigurationen erlaubt, nämlich der von Derrington, Krauskopf und Lennie (1984) entwickelte und nach ihnen benannten DKL-Farbraum, dem die auf Seite 
beschriebene auf den Rezeptorerregungen der L-, M- und S-Zapfen aufbauende Farbtafel von MacLeod und Boynton (1979) zugrunde liegt.
Derrington et al. (1984) postulieren aufgrund von Versuchen an der Retina von Makaken die Existenz von drei antagonistischen neuronalen Mechanismen, die die Achsen ihres Farbraums bilden: Eine chromatische Dimension, deren Ausprägung sich aus den Zapfenerregungen als S-(L+M) berechnet, wird als konstante S-Erregung 
bezeichnet und entspricht dem Gelb-Blau-Mechanismus. Der zweite chromatische Gegenfarben-Mechanismus, dessen Aktivierung als Differenz der Zapfenerregungen L-M bestimmt wird, nennt sich konstante L-M-Erregung 
und entspricht dem Rot-Grün-Mechanismus. Hinzu kommt noch eine dritte Achse 
, die die Leuchtdichte-Information enthält. Dieser achromatische Mechanismus hängt nicht von der Erregung des S-Systems ab und errechnet sich als Summe der Zapfenerregungen L+M. Diese drei antagonistischen Mechanismen bilden die Grundlage von rezeptiven Feldern. Das Modell von Derrington et al. (1984) postuliert außerdem eine Normierung zum Weißpunkt 
, der entweder dem energiegleichen Spektrum oder dem Farbort des Kontextes entspricht und als Ursprung des Gegenfarben-Koordinatensystems gewählt wird. Als Farbkoordinaten eines Reizes, die nun als DKL-Koordinaten bezeichnet werden, werden die Differenzen zu diesem Punkt auf den drei gerade beschriebenen Achsen eingesetzt. Die genaue Berechnung dieser DKL-Koordinaten wird im nächsten Abschnitt dargestellt.
Die Bestimmung der DKL-Farbkoordinaten aus den Normfarbwerten eines Reizes und seines Umfelds erfordert mehrere Rechenschritte, die nun entsprechend Brainard (1996) dargestellt werden. Den Ausgangspunkt bilden die Differenzen 
, 
und 
zwischen den von Reiz und Kontext hervorgerufenen Rezeptorerregungen, die nach Brainard (1996) mit den Differenzen 
, 
und 
der Normfarbwerte von Reiz und Kontext folgendermaßen zusammenhängen:
Aus der Gleichung 1.15 lassen sich Vorhersagen über die Aktivierung der hier als 
bezeichneten drei Mechanismen berechnen, wobei die Konstanten 
, 
und 
die Einheit des jeweiligen Reaktionssystems festlegen: Die Erregung des achromatischen Mechanismus berechnet sich nach der zweiten Zeile von Gleichung 1.15, die die mit der Leuchtdichtedifferenz gleichgesetzte Erregungsdifferenz angibt:
Für den L-M-Mechanismus wird nach Brainard (1996) hier eine gewichtete Differenz 
bestimmt, die auch vom Hintergrund abhängt, wobei 
eine gewichtete Summe aus der Erregungsdifferenz zwischen L- und M-System und der Erregung des L-Systems bezeichnet:
Die Aktivierung des S-Mechanismus hängt nach Brainard (1996) ebenfalls vom Kontext ab. 
ist eine gewichtete Summe aus der Erregungsdifferenz zwischen S- und achromatischem System und der Erregung des S-Systems:
Aufgrund dieser Vorüberlegungen können nun aus den Zapfenerregungs-Differenzen 
und die Reaktionen der drei Gegenfarben-Mechanismen berechnet werden. Brainard (1996) setzt dazu 
und 
und gelangt so zu folgender Transformation vom Raum der Rezeptorerregungen in den DKL-Raum:
Er empfiehlt, so zu wählen, daß 
dem Helligkeitskontrast C entspricht, der beispielsweise aus den Kontrasten der Zapfenerregungen 
, 
und 
berechnet werden kann (diese und andere Varianten werden von Brainard (1996, S. 568) diskutiert):
Derrington et al. (1984) wählen die Werte von und so, daß die maximal in ihrem Versuchsaufbau realisierbaren Erregungen 
und den Wert 1.0 erhalten. Brainard (1996) schlägt eine andere Möglichkeit zur Bestimmung der Skalierungsfaktoren für die drei Achsen vor: Er normiert die drei Mechanismen durch geeignete Wahl der Konstanten 
und so, daß sich bei isolierter Erregung eines der drei Systeme durch einen Reiz mit einem Helligkeitskontrast von einer Einheit jeweils der Wert Eins für die Reaktion des Gegenfarben-Systems ergibt. Nach Gleichung 1.16 gelangt man dabei zu folgenden Formeln zur Bestimmung dieser Normierungsfaktoren:
Die Differenzen der Erregung der antagonistischen Systeme lassen sich damit aus den Differenzen der Rezeptorerregung nach der folgenden Gleichung berechnen:
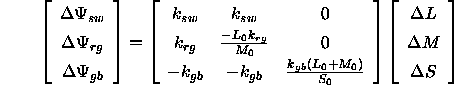
Die Erregungsdifferenzen der Gegenfarben-Kanäle lassen sich auch direkt durch Anwenden von Gleichung 1.15 aus den Normfarbwerten von Reiz und Hintergrund bestimmen. An diesem Farbmodell kann kritisiert werden, daß die Berechnung der Skalierungsfaktoren , und 
nicht aus theoretischen Gründen erfolgt, sondern nur aus Plausibilitätsgründen auf die hier beschriebene Weise stattfindet. Bei der Interpretation der Einheiten der Achsen in diesem Farbraum sollte dies immer berücksichtigt werden. Ähnliches gilt für die Berechnung des Helligkeitskontrastes, der ja ebenfalls an der Normierung der Achsen beteiligt ist.
Gleiche Farbart bei unterschiedlicher Leuchtdichte im DKL-Raum: Hier ist die Erregungsdifferenz der beiden chromatischen Gegenfarben-Systeme für die drei im Experiment verwendeten monochromatischen Reize (Wellenlänge 555, 580 und 640 nm) im DKL-Raum eingetragen. Jede der drei Linien beginnt bei einer Leuchtdichte des monochromatischen Reizes von 0.5 
und endet bei 7.0 
. Den Berechnungen wird als Umfeld der auch im Experiment verwendete Ausgangskontext mit den xyL-Koordinaten (0.25, 0.35, 2.0) zugrundegelegt.
Betrachtet man im DKL-Raum einen Reiz vor einem festen Kontext und variiert nur dessen Leuchtdichte, dann liegen alle diese Variationen auf einer Gerade, die außerdem durch den Ursprung geht, wie an dem Beispiel in Abbildung 1.5 zu sehen ist. Ein derartiges Muster in den bei Farbabgleichen erhobenen Daten würde damit bedeuten, daß die Verhältnisse der Erregungsdifferenzen genau repliziert werden können, wobei allerdings die Leuchtdichte der Einstellungen stärkeren Schwankungen unterliegt. Wie man in Abbildung 1.6 sehen kann, liegen bunttongleiche Farben, die sich nur in ihrer Sättigung unterscheiden, sowohl in der Normfarbtafel als auch im DKL-Raum alle auf einer Strecke, deren Endpunkte die Farbvalenzen des monochromatischen Reizes und das hinzugemischten ``Weiß'' bilden. Auch Sättigungsunterschiede führen also im DKL-Raum zu Koordinaten, die auf einer Geraden liegen; diese Geraden treffen sich für verschiedene Reize jeweils im Weißpunkt.
Bunttongleiche Farben in der Normfarbtafel und im DKL-Raum: Diese Abbildung zeigt die Farborte in der Normfarbtafel (links) und im DKL-Raum (rechts) von verschiedenen monochromatischen Reizen sowie die Strecken, auf denen die Mischungen dieser monochromatischen Reize mit einem ``weißen'' Reiz liegen, der dem im Experiment verwendeten Entsättigungsreiz mit den Koordinaten x= 0.4170 und y = 0.3935 entspricht. Sowohl für den Kontext als auch für den Zielreiz wird dabei von einer konstanten Leuchtdichte von 3 ausgegangen.
Der DKL-Raum der Gegenfarben eignet sich zur Repräsentation von Farben besonders gut, wenn deren Kontextabhängigkeit berücksichtigt werden soll. Die Darstellung dieses Farbraums durch Brainard (1996) umfaßt alle für die Bestimmung der DKL-Koordinaten erforderlichen Rechenschritte. Diese Theorie ist dadurch so genau spezifiziert, daß sie sich auch direkt zur Untersuchung von Kontexteffekten anwenden läßt.
Den aus Rezeptorkurven- und Gegenfarben-Theorien entwickelten Farbräumen, die in den letzten Abschnitten beschrieben sind, liegen letztlich spektrale Empfindlichkeitskurven zugrunde, die alleine aus Urteilen über die Gleichheit von Farben bestimmt werden können. Deshalb lassen sich aus diesen Theorien keine Aussagen über die Größe von Farbunterschieden ableiten. Die Linienelement-Theorien sind der Versuch einer solchen höheren Farbmetrik, d.h. einer Farbmetrik, die nicht nur Gleichheit bzw. Verschiedenheit von Farben behandelt, sondern Farben so quantifiziert, daß sich ein numerisches Maß für Farbunterschiede bestimmen läßt. Empirische Basis sind nicht mehr - wie bei der niederen Farbmetrik - Urteile über die Gleichheit bzw. Verschiedenheit von Farben, sondern ebenmerkliche Farbunterschiede.
Die Grundidee der Linienelement-Theorien im Farbraum geht auf Helmholtz (1891) zurück, der davon ausgeht, daß die Unterschiedsschwelle der drei Farbsysteme nach dem Weberschen Gesetz von deren Erregungsniveau abhängt und für mittlere Leuchtdichte-Niveaus etwa konstant ist. Dann läßt sich ein ebenmerklicher Farb-Unterschied (bzw. das Linienelement d s) wie folgt berechnen:
Die nach diesem Modell errechneten Spektralwertkurven 
stimmen jedoch nicht mit den heute bekannten Absorptionsspektren der drei Farbpigmente überein. Schrödinger (1920) versucht die Unzulänglichkeiten der Helmholtzschen Theorie durch folgende Änderung auszubessern:
wobei 
, 
und 
nicht näher spezifizierte Farbkoordinaten sein sollen. Schrödinger legt seinen Berechnungen die König-Fundamentals als spektrale Empfindlichkeitskurven zugrunde. Bei geeigneten Schätzwerten für die metrischen Koeffizienten 
stimmen die vom daraus bestimmten Linienelement vorhergesagten Hellempfindlichkeiten und die empirisch ermittelte Hellempfindlichkeitsfunktion 
gut überein.
Stiles (1946) modifiziert die Helmholtzsche Linienelement-Theorie ebenfalls, aber nicht so drastisch wie Schrödinger: Aufgrund der von ihm empirisch belegten Tatsache, daß für die drei visuellen Mechanismen unterschiedliche Weber-Brüche vorliegen, postuliert Stiles (1946) aufbauend auf empirisch bestimmten Farbwertkurven 
folgendes Linienelement:
wobei für den von ihm untersuchten Beobachter 
, 
und 
gilt. Bei hohen Leuchtdichten reduziert sich das in Gleichung 1.19 definierte Linienelement zu folgender, dem Helmholtzschen Linienelement in Gleichung 1.18 ähnlichen Form:
Dieses Linienelement sagt einige empirische Befunde gut vorher, beispielsweise ebenmerkliche Wellenlängenunterschiede, spektrale Hellempfindlichkeiten und Farbunterschiedsschwellen in Form von MacAdam-Ellipsen. Zwischen den unter anderem von MacAdam (1942b) experimentell bestimmten Diskriminationsellipsen und den von diesem Linienelement vorhergesagten ergeben sich aber prinzipielle Unterschiede: Die Gaußsche Krümmung (siehe Gray, 1993) des von Stiles (1946) vorhergesagten Linienelementes ist immer negativ, während die empirisch bestimmte manchmal negativ und manchmal positiv ist. Es läßt sich also prinzipiell keine isometrische Transformation finden, die die empirische und die aus dem Linienelement vorhergesagte Oberfläche gleichen Farbabstandes ineinander überführt (siehe hierzu auch Wyszecki & Stiles, 1982).
Trabka (1968a, 1968b) wendet die Konzepte der Signalentdeckungstheorie auf das Linienelement von Stiles (1946) an. Er betrachtet die einzelnen Zapfen als nicht-ideale Empfänger elektromagnetischer Schwingungen und alle Rezeptoren eines Typs zusammen als einen Detektor-Mechanismus. Außerdem nimmt Trabka (1968a) an, daß mit dem Signal-Rausch-Abstand auch die Veränderung des Outputs der Detektor-Mechanismen zunimmt und somit auch der wahrgenommene Abstand zwischen den zwei Farben. Das Linienelement berechnet sich dann als Summe des Signal-Rausch-Abstands am Output von verschiedenen Rezeptoren, die sich nur in ihrer spektralen Absorptionsfunktion und in ihrem Verstärkungsmechanismus unterscheiden.
Von Vos und Walraven (1972a, 1972b) stammt die komplexeste Linienelement-Theorie, die auf dem Konzept der Gegenfarben aufbaut. Sie nehmen an, daß Farbunterscheidbarkeit durch Variabilität in der Absorption von Photonen begrenzt wird und daß bei höheren Leuchtdichten Sättigungs- bzw. Übersättigungs-Phänomene auftreten können, die dazu führen, daß das Farbdiskriminationsvermögen nicht so hoch ist wie alleine aufgrund der Varianz in den Farbkanälen zu erwarten wäre. Die Signale der Gegenfarben-Kanäle vereinigen sich in einer positiv definiten quadratischen Form zu einem Output-Signal, das direkt proportional zum ebenmerklichen Unterschied zwischen zwei Reizen ist. Mit diesem Modell lassen sich Daten zur Farbdiskrimination recht gut vorhersagen, sowohl was die Wellenlängen-Diskrimination betrifft als auch bezüglich der Farbton-Unterscheidbarkeit.
Einige der hier vorgestellten Linienelement-Theorien können das Farbdiskriminationsvermögen relativ gut vorhersagen. Dadurch kann ein Farbraum so transformiert werden, daß gleiche Abstände in diesem Farbraum auch gleiche Farbunterschiede bedeuten. Wandell (1985) weist allerdings darauf hin, daß dies nur für konstante Beobachtungsbedingungen gilt, da die metrischen Koeffizienten des Linienelements vom Adaptationszustand des Auges abhängig sind. Wird dieser aber konstant gehalten, dann läßt sich die Unterscheidbarkeit zweier Reize alleine aus der Differenz der die beiden Reize repräsentierenden Vektoren bestimmen. Wandell (1982, 1985) bezeichnet diese Überlegung als Vektordifferenz-Hypothese und betrachtet sie als Spezialfall des Linienelements.
Zur Vorhersage der Ergebnisse in dem hier zu beschreibenden Experiment sind die Linienelement-Theorien nur bedingt geeignet, da sie eben keine Kontexteffekte berücksichtigen. Außerdem lassen sich aus diesen Theorien keine Vorhersagen über mögliche Auswirkungen der später ausführlich diskutierten Gedächtnismethode ableiten.
