Ein physiologischer Farbraum

Die von der CIE eingeführte Normfarbtafel basiert auf den imaginären Primärfarben X, Y, Z; unter Umständen ist es aber sinnvoller, direkt von der Erregung der verschiedenen Rezeptorsysyteme auszugehen. Smith und Pokorny (1996) beschreiben, wie man auf der Grundlage der König-Fundamentals einen geeigneten Farbraum aufbauen kann. Als Beispiel für derartige Farbräume sollen kurz der auf Rezeptorebene ansetzende Farbraum von MacLeod und Boynton (1979) sowie etwas ausführlicher der auch auf der Ebene der Gegenfarben angesiedelte DKL-Farbraum von Derrington, Krauskopf und Lennie (1984) näher beschrieben werden.

Ein auf Rezeptorempfindlichkeiten aufbauender Farbraum

MacLeod und Boynton (1979) stellen einen Farbraum vor, der direkt auf physiologischen Messungen aufbaut: Man kann Farben als Punkte in einem dreidimensionalen Raum auffassen, dessen Achsen durch die Erregung der drei Rezeptortypen L, M und S gegeben sind. MacLeod und Boynton (1979) halten dabei eine zweidimensionale Projektion dieses Raumes für besonders sinnvoll:

Sie gehen von der Annahme aus, daß die Rezeptoren des S-Systems nicht zur Gesamtleuchtdichte beitragen und daß die Summe der Eregungen von L und M konstant sei und somit gleich Eins gesetzt werden kann. Dann lassen sich die Koordinaten einer Farbe in diesem Raum folgendermaßen repräsentieren:

MacLeod und Boynton (1979) nennen folgende Vorteile dieser Darstellungsweise:

• Die Erregung der einzelnen Rezeptorsysteme ist direkt repräsentiert.
• Gleichen Entfernungen auf einer Linie in dieser Farbtafel entsprechen gleiche Veränderungen der Rezeptor-Erregungen für die drei Zapfenaretn.
• Die Schwerpunktregel läßt sich direkt anwenden: Die Leuchtdichte einer Mischung von zwei Farben mit den Leuchtdichten n und m beträgt n + m und der Farbort der Mischung teilt die Strecke zwischen den Farbörtern der beiden gemischten Farben im Verhältnis n:m.

Der DKL-Farbraum der Gegenfarben

 

Der nach seinen Urhebern benannte DKL-Farbraum von Derrington, Krauskopf und Lennie (1984) wurde aus der gerade beschriebenen Farbtafel entwickelt: Es werden die Achsen konstante S-Erregung (entspricht dem Gelb-Blau-Mechanismus) und konstante L-M-Erregung (entspricht dem Rot-Grün-Mechanismus) verwendet; hinzu kommt noch eine dritte Achse , die die Leuchtdichteinformation enthält. Dieser achromatische Mechanismus hängt nicht von der Erregung des S-Systems ab, nur das L- und das M-System liefern Helligkeitsinformation. Diese verschiedenen antagonistischen Mechanismen bilden die Grundlage von rezeptiven Feldern.

Abbildung 2 soll den Zusammenhang zwischen den Rezeptorsystemen und den drei Farbmechanismen, wie er auch von den meisten anderen Gegenfarb-Theorien postuliert wird, nochmals verdeutlichen. Das Modell von Derrington et al. (1984) postuliert eine Normierung zum Weißpunkt, der normalerweise dem energiegleichen Spektrum entspricht: Dieser wird als Ursprung des Gegenfarb-Koordinatensystems gewählt. Als Farbkoordinaten eines Reizes werden die Differenzen zum Weißpunkt auf den drei Achsen eingesetzt.

 
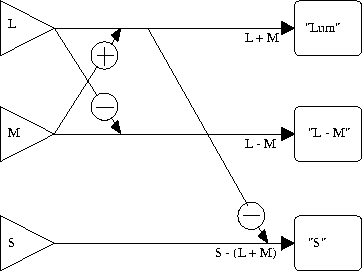
Abbildung 2:   Die Mechanismen des DKL-Farbraumes: Diese Abbildung zeigt, wie die Signale der Rezeptorsysteme L, M und S verschaltet sind, um die drei Gegenfarb-Systeme ``Lum'' (Weiß-Schwarz), ``L - M'' (Rot-Grün) und ``S'' (Gelb-Blau) zu bilden. Ein Pluszeichen bedeutet, daß die Erregung der Rezeptoren summiert wird, ein Minuszeichen, daß Erregungsdifferenzen gebildet werden.

Auf der Grundlage von Versuchen an der Retina von Makaken im Rahmen dieses Modells beschreiben Derrington et al. (1984) zwei Klassen von Neuronen: Eine Art der Neurone bezieht ihren Input nur aus L- und M-Zapfen, die andere aus S-Zapfen zusammen mit unterschiedlich gewichtetem Input aus L- und M-Zapfen (siehe hierzu die Abbildung 2). Bei den rezeptiven Feldern der Neurone der ersteren Art finden sich außerdem unterschiedliche Beiträge der L- und M-Zapfen zum Zentrum und zum Umfeld. Es können Gegenfarb-Systeme nachgewiesen werden.

Grundlage des DKL-Raumes sind ja die Differenzen zwischen einem Reiz mit den Farbwerten (X, Y, Z) und dessen Hintergrund mit den Farbwerten ; man betrachtet also

analog ergibt sich die Aktivierung der L-, M- und S-Rezeptorsysteme als

wobei (L, M, S) die Aktivierung durch den Reiz und die Aktivierung der Zapfensysteme durch den Hintergrund bezeichnen. In diesem Sinne wird der Reiz als ein (achsenweises) Inkrement bzw. Dekrement zum Hintergrund betrachtet.

Nach Brainard (1996) gilt nun folgender Zusammenhang zwischen den Farbwert-Differenzen und den Erregungs-Differenzen der Rezeptorsysteme:
 

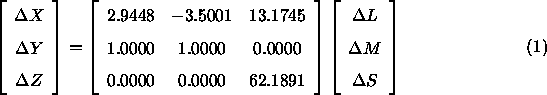
Umgekehrt muß dann auch gelten:

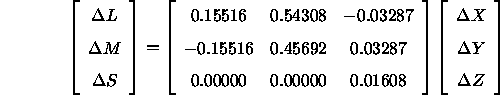
Der in den folgenden Fromeln häufig erscheinende Term entspricht genau der Leuchtdichte des Kontextes, wie sich bei der Berechnung von , und für ein Umfeld mit den Koordinaten sehen läßt:

entspricht dann der Summe

und somit, wie oben behauptet, der Leuchtdichte des Kontextes. Aus der Gleichung 1 lassen sich Vorhersagen über die Aktivierung der hier als bezeichneten drei Mechanismen berechnen:

Achromatischer Mechanismus : Berechnung aus der zweiten Zeile von Gleichung 1 durch

wobei die frei wählbare Konstante die Einheit des achromatischen Reaktionssystems festlegt.

L-M-Mechanismus : Nach Brainard (1996) wird hier eine gewichtete Differenz bestimmt durch

wobei die frei wählbare Konstante die Einheit des L-M-Reaktionssystems festlegt und eine gewichtete Summe aus der Erregungsdifferenz zwischen L- und M-System und der Erregung des L-Systems ist. Bemerkenswert hierbei ist, daß der Wert von vom Hintergrund abhängig ist.

S-Mechanismus : Nach Brainard (1996) gilt hier

wobei die frei wählbare Konstante die Einheit des S-Reaktionssystems festlegt und eine gewichtete Summe aus der Erregungsdifferenz zwischen S- und achromatischem System und der Erregung des S-Systems ist. Auch hängt vom Umfeld ab.

Aufgrund dieser Vorüberlegungen können nun aus den Zapfenerregungs-Differenzen und die Reaktionen der drei Gegenfarbmechanismen berechnet werden. Brainard (1996) setzt dazu und und gelangt somit zu folgender Umrechnungsformel der Rezeptorerregungsdifferenzen in den DKL-Raum:
 

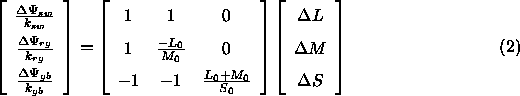
Brainard (1996) empfiehlt, so zu wählen, daß dem Helligkeitskontrast C entspricht, der beispielsweise folgendermaßen berechnet werden kann (diese und andere Varianten werden von Brainard, 1996, S. 568 diskutiert):
 

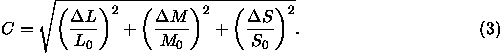
Zur Berechnung des Helligkeitskontrastes werden also die Kontraste , und der drei Zapfenerregungen eingesetzt. Beim Übergang vom Zapfenerregungs-Raum in den Zapfen-Kontrast-Raum findet eine Verschiebung des Ursprungs (es werden nur noch Differenzen betrachtet) und eine Skalierung der Achsen (Umfeld als Standard) statt; Brainard (1996) bezeichnet diese Transformation als von Kries-Webersche Normierung.

Derrington et al. (1984) setzen die Werte von und so, daß die maximal in ihrem Versuchsaufbau realisierbaren Erregungen und den Wert 1.0 erhalten. Brainard (1996) empfiehlt eine andere Möglichkeit zur Bestimmung der Skalierungsfaktoren für die drei Achsen: Er normiert die drei Mechanismen durch die Wahl geeigneter Konstanten und so, daß sich bei isolierter Erregung eines der drei Systeme durch einen Reiz mit Einheits-Helligkeitskontrast jeweils der Wert Eins für die Reaktion des Gegenfarb-Systems ergibt: Man erhält diese Skalierungsfaktoren ausgehend von der Inversen der Transformationsmatrix von den Differenzen der LMS-Koordinaten in die Differenzen der DKL-Koordinaten; diese Inverse lautet

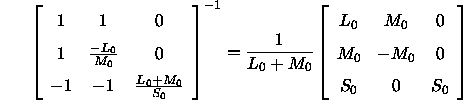
Die erste Spalte bezeichnet die Differenzen der Zapfenerregungen , bei denen nur das achromatische System reagiert; die zweite Spalte gibt die Differenzen der Zapfenerregungen an , bei denen nur das L-M-System reagiert und die dritte Spalte gibt schließlich die Differenzen der Zapfenerregungen an, bei denen nur das S-System reagiert. Nun berechnet man für jede dieser drei Spalten (die ja auch eine Zapfenerregungsdifferenz vor dem Standard-Hintergrund bezeichnen) einzeln den Helligkeitskontrast nach Gleichung(3; dieser Helligkeitskontrast entspricht den gesuchten Normierungsfaktoren , und , die dafür sorgen, daß die Reaktion des DKL-Systems auf die vorher berechneten Einheits-Reize auch genau den Wert Eins annimmt.

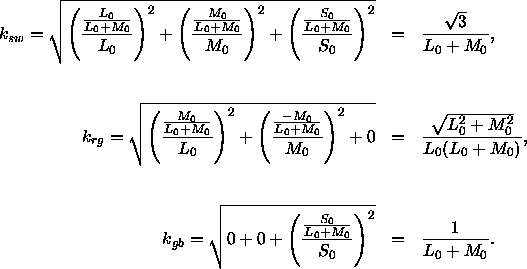
Somit erhält man die Transformationsmatrix

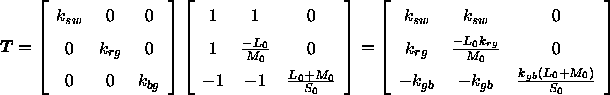
Die Differenzen der Erregung der antagonistischen Systeme lasse sich somit aus den Differenzen der Rezeptorerregung nach der folgenden Gleichung berechnen:

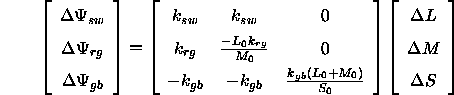
Schließlich lassen sich die Reaktionen des Gegenfarb-Systeme auch aus den Differenzen der Farbwerte direkt unter Verwendung der Assoziativität der Matrixmultiplikation vorhersagen:

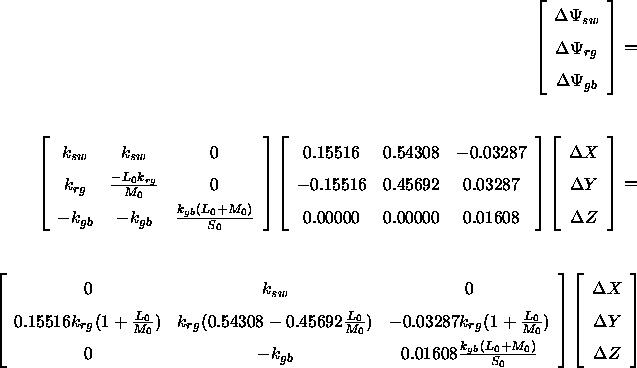
Nach Ausmultiplizieren und Vereinfachen erhält man:
 

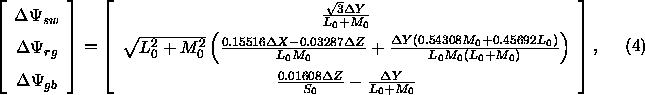
An diesem Farbmodell kann kritisiert werden, daß die Berechnung der Skalierungskonstanten , und nicht aus theoretischen Gründen eindeutig festgelegt ist, sondern nur aus Plausibilitätsgründen auf die hier beschriebene Weise stattfindet. Bei der Interpretation der Einheiten der Achsen in diesem Farbraum sollte dies immer berücksichtigt werden. Ähnliches gilt für die Berechnung des Helligkeitskontrastes, der ja auch an der Normierung der Achsen beteiligt ist.

zurück zur Hauptseite (Theorien der Farbwahrnehmung)
zurück zu meiner homepage

Anmerkungen und Mitteilungen an

Last modified 11-5-98