Die Linienelement-Theorien sind der Versuch einer höheren Farbmetrik, d.h. einer Farbmetrik, die nicht nur Gleichheit bzw. Verschiedenheit von Farben behandelt, sondern auch Farben so quantifiziert, daß sich ein numerisches Maß für Farbunterschiede bestimmen läßt. Empirische Basis sind nicht mehr - wie bei der niederen Farbmetrik - Urteile über die Gleichheit bzw. Verschiedenheit von Farben, sondern es werden ebenmerkliche Unterschiede zugrunde gelegt. Die Grundidee der Linienelement-Theorien im Farbraum geht auf von Helmholtz (1867) zurück. Er versuchte, die Farben so zu ordnen, daß jeweils zwischen Paaren von ihnen der selbe wahrnehmungsmäßige Unterschied besteht (z.B. ein ebenmerklicher Unterschied), um daraus eine Metrik der Farben abzuleiten.
Bei einer Farbmetrik sollen die Abstände im metrischen Raum zwischen zwei Punkten dem wahrgenommenen Unterschied zwischen den durch diese beiden Punkte repräsentierten Farben entsprechen. Subjektive Unterschiede zwischen relativ ähnlichen Farben lassen sich durch eine gewichtete Summe der quadrierten Differenzen der Farbkoordinaten beschreiben; geometrisch bedeutet dies, daß die ebenmerklichen Unterschiede kleine Ellipsoide bilden. Im dreidimensionalen euklidischen Raum ist beispielsweise der Abstand 
zwischen zwei Punkten 
(mit den Koordinaten 
) und 
(mit den Koordinaten 
) folgendermaßen definiert:
Man kann aber auch komplexere Abstandsmetriken festlegen, z.B. die folgende auf der quadratischen Form 
aufbauende:
Hier sind die metrischen Koeffizienten 
eine beliebige kontinuierliche Funktion der Koordinaten von , die diese quadratische Form positiv und definit machen, so daß das Abstandsmaß bei allen Punkten und für beliebige 
positiv ist. Die hängen dadurch nur vom jeweiligen Punkt ab; bei der praktischen Anwendung dieses Abstandsmaßes besteht das Hauptproblem in der Bestimmung dieser metrischen Koeffizienten.
Ein Raum, in dem das so definierte ein Abstandselement bezeichnet - also ein Linienelement - nennt man einen Riemannschen Raum. Unter bestimmten Bedingungen läßt sich ein Riemannscher Raum so transformieren (meist nichtlinear), daß für die transformierten Koordinaten 
ein euklidisches Abstandsmaß 
gilt; Wyszecki und Stiles (1982) bezeichnen solche Räume ebenfalls als (im weiteren Sinne) euklidisch.
Nun soll also ein Linienelement so definiert werden, daß es gerade dem ebenmerklichen Unterschied zwischen zwei beliebigen Farben entspricht und außerdem für alle Paare von Farben, die sich um eine Ebenmerklichkeit voneinander unterscheiden, den selben Wert annimmt. Wird eine Farbe 
als Ausgangspunkt gewählt, dann beschreiben die um entfernten Farben nach Gleichung 5 ein Ellipsoid mit als Mittelpunkt.
In diesem Abschnitt sollen die für die Linienelement-Theorie des Farbensehens wichtigen grundlegenden geometrischen Begriffe (anschaulich) erläutert werden.
Grundlage der Riemannschen Geometrie ist das Linienelement, das sich allgemein schreiben läßt als
wobei F(x,y) > 0 für 
und F definiert ist durch
Für gewöhnliche Oberflächenpunkte ist das Linienelement positiv definit.
Unter einer Riemannschen Metrik, auch als metrischer Tensor
bezeichnet, versteht man eine Funktion, die ein Berechnungsverfahren für den Abstand zweier Punkte in einem gegebenen Raum angibt. Die einzelnen Komponenten des metrischen Tensors können als Skalierungsfaktoren für die Koordinatendifferenzen (
bzw. 
) betrachtet werden.
Das Konzept der Krümmung einer Oberfläche läßt sich folgendermaßen veranschaulichen: Nimmt man beispielsweise die Oberfläche einer Kugel, so läßt sich diese nicht flach auf einer Ebene ausbreiten ohne daß die ``zerknittern'' würde; man kennt dies vielleicht von Orangenschalen; dies gilt auch für Ausschnitte aus der Oberfläche. Je schmaler die Ausschnitte gewählt werden, desto geringere Verzerrungen treten beim Flachdrücken (d.h. beim Projizieren in die Ebene) auf.
Mit dem mathematischen Konzept der Gaußschen Krümmung, dessen Eigenschaften und Berechnungsvorschriften beispielsweise von Gray (1993) dargestellt werden, läßt sich bestimmen, welche Oberflächen ineinander überführt werden können, d.h. durch ``Verbiegen'' gleich gemacht werden können, ohne daß sie verzerrt werden. Bei der Gaußschen Krümmung handelt es sich um eine intrinsische Eigenschaft einer Oberfläche; diese bleibt erhalten, wenn die Oberfläche ``verbogen'' wird (bei Stauchung oder Streckung dagegen nicht). Eine Oberfläche, die sich in alle Richtungen ausbeult, nennt man positiv gekrümmt: Für beliebige Punkte der Oberfläche muß gelten, daß alle anderen Punkte der Oberfläche auf der selben Seite einer Ebene liegen, die die Oberfläche an diesem Punkt berührt. Eine flache Ebene und die Oberfläche eines Zylinders oder eines Kegels besitzen die Krümmung Null, sattelförmige Oberflächen weisen dagegen eine negative Krümmung auf. Die Gaußsche Krümmung bezeichnet das dazugehörige numerische Maß; sie entspricht dem Winkel, mit dem sich ein Oberflächenausschnitt öffnet, der in der Ebene ``flachgedrückt'' wird, wenn er an einer Seite aufgeschnitten ist. Konstante Gaußsche Krümmung läßt sich anschaulich so darstellen: Ein unelastisches Netz, das sich um einen Teil der Oberfläche eine Körpers mit konstanter Gaußscher Krümmung schließen läßt, passt um den gesamten Körper (dies besagt das sogenannte Gauß Theorema Egregium). Etwas formaler ist nun die folgende Darstellung:
Zur Bestimmung der Krümmung einer Oberfläche muß sichergestellt sein, daß diese kontinuierlich ist und keine Sprungstellen besitzt. Dann betrachtet man für einen bestimmten Punkt alle Ebenen, die diesen Punkt enthalten und senkrecht zu der diesen Punkt enthaltenden Tangenten-Ebene sind. Der Schnitt dieser Ebenen mit der Oberfläche ergibt jeweils eine Kurve, die wiederum in dem betreffenden Punkt eine bestimmte Krümmung besitzt. Bezeichnet man nun die geringste aller dieser Krümmungen mit 
und die größte mit 
, so berechnet sich die Gaußsche Krümmung K der Oberfläche in diesem Punkt durch
Die mittlere Krümmung einer Oberfläche in einem Punkt wird dagegen als 
berechnet. Die beiden Krümmungen und werden auch als Hauptkrümmungen (principal curvatures) bezeichnet.
Es ist möglich, den absoluten numerischen Wert der Gaußschen Krümmung zu berechnen als Grenzwert eines Raumwinkels geteilt durch eine Fläche. In diesem Sinne kann man die Gaußsche Krümmung auch als Flächendichte der Krümmung betrachten (ich stelle mit das wie bei einer etwas elastischen Oberfläche, z.B. eines Luftballons, vor: bei hoher positiver Krümmung wird die Oberfläche besonders gespannt und also ``dünner'', bei negativer Krümmung schiebt sie sich dagegen etwas zusammen).
Die Gaußsche Krümmung läßt sich auch vollständig aus der ersten Fundamentalform bzw. dem Linienelement
berechnen, wobei E, F, G die Koeffizienten der ersten Fundamentalform sind und 
eine Diskriminante:
wobei 
die Verbindungs-Koeffizienten (connection coefficients) sein sollen. Eine weitere Möglichkeit zur Berechnung der Gaußschen Krümmung ist nach Gray (1993, S. 285) die folgende:
Die Distanz zweier mehr als ebenmerklich verschiedener Farben und (bzw. das entsprechende Linienelement) läßt sich nach folgendem Verfahren konstruieren, das auf Schrödinger (1920) zurückgeht: Man stelle sich verschiedene beliebige Linien vor, die diese beiden Punkte im Farbraum verbinden. Dann kann diejenige Linie, auf der die wenigsten ebenmerklichen Unterschiede liegen, als wahrnehmungsmäßige Distanz der beiden Farben interpretiert werden; als numerischer Wert wird hierfür die Anzahl der ebenmerklichen Unterschiede eingesetzt. Mathematisch kann dieses Maß durch Integrieren des Linienelements zwischen den beiden Punkten und entlang der geodätischen Linien und anschließende Division durch eine Normierungskonstante (nämlich den Wert des ebenmerklichen Unterschieds) beschreiben. Im euklidischen Raum handelt es sich bei diesen geodätischen Linien um Geraden zwischen den beiden Punkten, im allgemeinen Fall eines Riemannschen Raums dagegen meist um gekrümmte Linien.
Mit solchen Linienelementen lassen sich auch Konturen gleicher Ausprägungen einzelner Farbattribute im Farbraum darstellen, wenn sich ein Zusammenhang zwischen einer geometrischen Eigenschaft und dem entsprechenden Farbattribut finden läßt. Dabei können die Farbkoordinaten sowohl als Transformation der Rezeptorerregungen als auch als Transformation der Erregung der Gegenfarb-Kanäle festgelegt werden; Wyszecki und Stiles (1982) beschreiben die letztere Betrachtungsweise als die plausiblere und gebräuchlichere. Nach Schrödinger (1920) lassen sich Gleichheitskonturen für die Farbattribute Helligkeit, Farbton und Buntheit folgendermaßen bestimmen:
vom Ursprung entfernt ist, desto heller wird er empfunden; ist die Entfernung zwischen zwei Punkten und entlang einer geodätischen Linie minimal, erscheinen die beiden zugehörigen Farben gleich hell. Hält man nun den Punkt fest, läßt sich auf jedem Strahl vom Ursprung weg ein Punkt finden, der bei gleicher Entfernung zum Ursprung minimal vom Punkt entfernt ist. Alle derartigen Punkte zusammen definieren eine Oberfläche im Farbraum, die als Kontur gleicher Helligkeit zu aufgefaßt werden kann. Dieses Verfahren läßt sich für verschiedene Entfernungen zum Ursprung und somit für verschiedene Helligkeiten durchführen.
haben, der einem achromatischen Reiz mit der entsprechenden Helligkeit entspricht. Diese Linien lassen sich nun wieder für verschiedene Helligkeiten ermitteln; alle diese Linien zusammen bilden dann eine Kontur konstanten Farbtons.
liegt, der den achromatischen Reiz entsprechender Helligkeit entspricht.
Eine zentrale Frage in diesem Zusammenhang lautet, ob sich ein dreidimensionaler Riemannscher Raum mit gegebenen Linienelementen auf einen dreidimensionalen euklidischen Raum abbilden läßt oder in diesen eingebettet werden kann, unter der Restriktion, daß Gleichheit von Distanzen bewahrt bleibt. Dazu müßten sich drei Funktionen 
finden lassen, für die gilt
Diese Forderung wurde bereits oben für euklidische Räume im weiteren Sinne gestellt. Triff diese Forderung für einen Riemannschen Raum nicht zu, kann er dennoch in einen euklidischen Raum eingebettet werden, der dann allerdings eine Dimension m von mehr als drei besitzt:
Die maximale Dimension m eines euklidischen Raumes, auf den ein Riemannscher Raum der Dimension n abgebildet werden kann, berechnet sich nach der Gleichung
Für einen dreidimensionalen Riemannschen Raum wäre also maximal ein sechsdimensionaler euklidischer Raum erforderlich; für einen zweidimensionalen Riemannschen Raum würde hingegen ein dreidimensionaler euklidischer Raum ausreichen. Ein zweidimensionaler Riemannscher Raum liegt vor, wenn man nur Konturen gleicher Ausprägung eines Farbattributs (wie oben beschrieben) betrachtet. Farben gleicher Helligkeit lassen sich dann beispielsweise als Punkte auf einer Oberfläche in einem dreidimensionalen euklidischen Raum repräsentieren. Die Koordinaten dieser Punkte im euklidischen Raum wären eine Funktion der Farbwerte des Reizes und sie sind so gewählt sind, daß zwei Punkte, deren Distanz gleich ist, als gerade merklich verschieden empfunden werden (und umgekehrt).
Die charakteristischen Merkmale der Einbettung eines Raumes auf der Grundlage des Linienelements werden durch beliebige kontinuierliche Transformationen der Farbkoordinaten nicht verändert und lassen sich mathematisch durch die Gaußsche Krümmung bestimmen, die von den Koeffizienten des Linienelements abhängt: Für eine längentreue Abbildung eines Raumes in einen anderen Raum gleicher Dimension ist die selbe Gaußsche Krümmung aller einander entsprechenden Punkte notwendig und hinreichend; im euklidischen Raum beträgt diese immer Null. Findet man nun in einem Riemannschen Raum Punkte mit von Null verschiedener Krümmung, läßt sich dieser Raum auf keinen Fall in einen euklidischen Raum der selben Dimension abbilden.
Linienelemente lassen sich auch dann anwenden, wenn der Farbraum nicht euklidisch ist. Sie lassen sich durch Schwellenmessungen und Berechnung der Standardabweichung bei Farbabgleichen empirisch ermitteln. Hauptproblem ist die Bestimmung der metrischen Koeffizienten . Mittels einer induktiven Methode lassen sie sich aus Theorien zur Funktionsweise bestimmter visueller Mechanismen zusammen mit experimentell erhobenen Schwellen bestimmen; empirisch können die Koeffizienten als Funktion der Farbwerte ermittelt werden, indem Unterschiedsschwellen (oder Streuungsmaße bei Farbabgleichen) für weite Teile des Farbraums bestimmt werden.
Die Grundlage der Linienelement-Theorie von von Helmholtz bildet das Weber-Fechnersche Gesetz, das von Helmholtz (1867) zuerst nur auf die Wahrnehmbarkeit von Helligkeitsunterschieden anwendet. In der einfachsten Form formuliert er die Wahrnehmungsschwelle 
für einen Helligkeitsunterschied 
bei einer anfänglichen Helligkeit H entsprechend dem Weberschen Gesetz als 
, wobei A bei mittleren Beleuchtungsstärken als konstant angenommen wird. Dieses Modell wird dann dahingehend elaboriert, daß eine Abhängigkeit der Konstante A von der Helligkeit in der Form 
postuliert wird, wobei a und b Konstanten sind und b als sehr groß angenommen wird. Außerdem postuliert er noch ein ``Eigenlicht'' 
des Auges, das zur Helligkeit des Reizes hinzukommt. So gelangt er zur folgenden Formel für einen wahrnehmbaren Helligkeitsunterschied:
1891 entwickelt von Helmholtz dieses Modell weiter, indem er nicht die gesamte Helligkeit, sondern die Erregung der drei Farbsysteme betrachtet. Er entwickelt folgende Hypothese zur Deutlichkeit des Unterschieds zweier Farben (x, y, z) und 
wobei die Konstanten a, b, c die Farbwerte des ``Eigenlichts'' (also der Aktivität bei völliger Abwesenheit einer Reizgrundlage) bezeichnen. Ausgangspunkt seiner Überlegungen sind die kürzesten Farbenreihen, also ``diejenigen Reihen von Übergangsfarben zwischen zwei gegebenen Endfarben von verschiedener Qualität und Quantität..., für welche die Summe der wahrnehmbaren Unterschiede ein Minimum ist, welche Reihen also den kürzesten Linien im Farbensystem entsprechen würden'' (von Helmholtz, 1891, S. 1073). Mit dieser Theorie versucht von Helmholtz (1891) eine Reihe verschiedener empirischer Befunde zu erklären.
Von Helmholtz (1896) versucht, die metrischen Koeffizienten des Linienelements auf der Grundlage der drei-Komponenten-Theorie des Farbensehens und des Weberschen Gesetzes zu bestimmen: Dem Farbensehen liegen drei Zapfenmechanismen mit den spektralen Reaktionsfunktionen 
zugrunde, die sich als Linearkombinationen der drei empirisch bestimmbaren Farbwertkurven 
berechnen lassen:
Somit lauten die Reaktionen dieser drei Mechanismen auf eine Strahlung mit der spektralen Verteilung 
Helmholtz (1896) nimmt weiter an, daß die Unterschiedsschwelle dieser drei Mechanismen nach dem Weberschen Gesetz von deren Erregungsniveau abhängt; außerdem wird angenommen, daß für mittlere Leuchtdichte-Niveaus der Weber-Bruch etwa konstant ist, d.h. 
const. Außerdem wird angenommen, daß sich ein ebenmerklicher Unterschied (bzw. das Linienelement ) wie folgt berechnen läßt:
Zur Überprüfung dieser Vorstellung greift von Helmholtz auf die Koeffizienten 
aus Gleichung 6 zurück, die so gesetzt werden, daß sie empirische Ergebnisse zur Unterscheidbarkeit monochromatischer Reize unterschiedlicher Wellenlänge vorhersagen können. Die so errechneten Farbwertkurven stimmen jedoch nicht mit den heute bekannten Absorptionsspektren der drei Farbpigmente überein. Diese Linienelemente können deshalb nicht zutreffen, wenn jeder der drei Mechanismen nur einen Sehfarbstoff besitzt.
Vos und Walraven (1972a) leiten aus dem von Helmholtzschen Linienelement folgende Formel zur Bestimmung des ebenmerklichen Unterschieds zwischen einem monochromatischen Reiz mit den Koordinaten (R, G, B) und einem in der Wellenlänge um 
veränderten zweiten monochromatischen Reiz her:
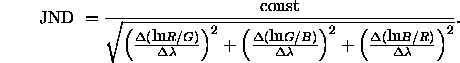
Die Helmholtzschen Linienelemente würden Konturen gleicher Helligkeit nach folgender Beziehung - die empirisch nicht haltbar ist - vorhersagen:
Schrödinger (1920) führt folgende drei Annahmen ein, auf denen das von ihm propagierte Linienelement basiert:
bezeichne die Verschiedenheit zwischen den beiden Farben 
und 
. Gilt nun 
, 
und 
, dann gilt für den quadrierten Abstand:
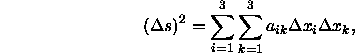
wobei die metrischen Koeffizienten 
in dieser Gleichung eine Funktion von 
sind und angenommen wird, daß 
. Diese quadratische Form beschreibt eine Ellipse und durch diese Gleichung ist eine riemannsche Metrik für die Mannigfaltigkeit von Zahlentripeln bestimmt, wenn man als das Linienelement dieser Mannigfaltigkeit auffaßt.
(und somit auch die ) als Differentiale angesehen werden (denn die variieren bei ebenmerklich verschiedenen Farben nicht so stark, daß Sprungstellen auftreten); außerdem hat für jedes ebenmerklich verschiedene Farbenpaar den selben Wert. Dies führt unter anderem dazu, daß die Diskriminationsellipsen gleich groß sind. Der konkret für gewählte Wert ist nicht von Bedeutung, es handelt sich nur um eine Normierungskonstante.
ab, die für die kürzeste Verbindungslinie (geodätische Linie) zwischen den beiden Farbpunkten bestimmt wird. Als kürzeste Linie wird diejenige verwendet, bei denen dieses Integral den kleinsten Wert annimmt. Zwei Farben sind damit um so ähnlicher, je weniger ebenmerkliche Unterschiede zwischen ihnen liegen, wenn man diese Zwischenstufen so wählt, daß jeweils eine minimale Anzahl solcher Schritte zwischen den beiden Endpunkten liegt.
Nun müssen die metrischen Koeffizienten bestimmt werden. Sie würden sich prinzipiell durch empirische Bestimmung der Unterschiedsempfindlichkeit für alle Richtungen, in die sich eine Farbe ändern kann, bestimmen lassen. Schrödinger (1920) hält diesen Weg jedoch für zu aufwendig; MacAdam (1942b) Brown und MacAdam (1949) und Brown (1957) beschreiten ihn aber später.
Zuerst wird auf der Grundlage der von Schrödinger (1920) behaupteten Additivität der Helligkeit h von Farben
folgende homogene Form für den Helligkeitsparameter bestimmt:
Diese Summe läßt die Kontur gleicher Helligkeit im Farbraum zu einer Ebene werden. Daraus entwickelt Schrödinger (1920) nun sein Linienelement, welches versucht, die Unzulänglichkeiten der von Helmholtzschen Theorie durch folgende Änderung auszubessern:
Die metrischen Koeffizienten sollen dabei folgendermaßen berechnet werden:
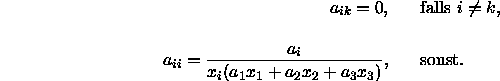
Schrödinger legt seinen Berechnungen die König-Fundamentals als spektrale Empfindlichkeitskurven der drei Mechanismen zugrunde und weist darauf hin, daß dieses Linienelement nur für die ``wahren Grundfarben'' gilt. Im Schrödingerschen Raum sind Leuchtdichte und Wellenlänge orthogonal zueinander; dies ist bei den von Helmholtzschen Linienelementen nicht der Fall.
Bei geeigneten Schätzwerten für 
stimmen die vom (nach Schrödinger bestimmten) Linienelemente vorhergesagten Helligkeiten und die empirisch ermittelte Hellempfindlichkeitsfunktion 
gut überein. Es läßt sich auch der Abney-Effekt vorhersagen, der Betzhold-Brücke-Effekt hingegen nicht, was Schrödinger (1920) damit begründet, daß seine Theorie auf der Fechnerschen aufbaut und deshalb nur in deren Gültigkeitsbereich zutrifft. Würden aber noch - ähnlich wie bei Helmholtz (1891) - Parameter für das ``Eigenlicht'' des Auges hinzugenommen, könnte sich auch dieses Phänomen durch Linienelemente beschreiben lassen.
Schrödinger (1920) zeigt auch selbst, daß sich die Daten zur Unterscheidbarkeit monochromatischer Reize unterschiedlicher Wellenlänge durch sein Linienelement gut vorhergesagt werden. Nach Vos und Walraven (1972a) bestimmt sich der ebenmerkliche Unterschied zwischen einem monochromatischen Reiz mit den Koordinaten (R, G, B) und einem zweiten monochromatischen Reiz, dessen Wellenlängenmaximum und verschoben ist, folgendermaßen:
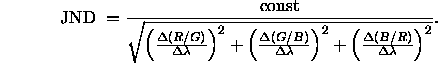
Zur Bestimmung der geodätischen Linien nimmt Schrödinger folgende Ersetzungen vor:
so daß die Gleichung für das Linienelement nun lautet
Im Raum der 
muß die Geodätische zwischen zwei Farben X und Y eine ebene Kurve in der Ebene 
sein, wie von Schrödinger (1920) gezeigt wird. Verändert man nur die Helligkeit eines Reizes, bewegt man sich auf einer Geodätischen. Schrödinger (1920) zeigt außerdem, daß sich das Verschiedenheitsmaß für zwei Farben Y und Z aus dem Helligkeitsunterschied und dem Farbunterschied zusammensetzt, wie z.B. in folgender Gleichung zu erkennen ist:
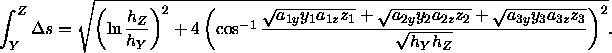
Schrödinger (1920) weist außerdem nach, daß die Menge aller geodätischen Linien auf einer Ebene konstanter Helligkeit genau der Menge der Ellipsen entspricht, die die Unterscheidbarkeit von Farben repräsentieren.
Stiles (1946) modifiziert die Helmholtzsche Linienelement-Theorie ebenfalls, aber nicht so drastisch wie Schrödinger: Er geht im wesentlichen von drei unabhängigen Mechanismen aus, die jeweils durch eine eigene spektrale Empfindlichkeitsfunktion gekennzeichnet sind. Um keine Interaktion der drei Mechanismen bei der Bestimmung des Linienelements zu erhalten, müssen die Primärreize so gewählt werden, daß jede genau einen Zapfenmechanismus (und nur diesen) erregt.; es kommen also nur imaginäre Primärreize in Frage.
Ausgangspunkt von Stiles (1946) sind die von ihm erhobenen Daten zur Farbdiskrimination: Auf ein 10
großes monochromatisches Umfeld der Wellenlänge 
und der Leuchtdichte 
wird für sehr kurze Zeit (63 Millisekunden) in der Mitte ein 1 großes monochromatisches Quadrat der Wellenlänge 
hinzuprojiziert und dabei wird die Schwelle für die Leuchtdichte 
bestimmt, ab der der Beobachter bei 50% der Darbietungen das Inkrement wahrnehmen kann. Nach wiederholten Messungen kann für den einen Beobachter eine Schar empirischer Funktionen von log
gegen log bestimmt werden. Unter Vernachlässigung der bei extrem hohen Leuchtdichten auftretenden Anomalien lassen sich diese Funktionen als Ergebnis von drei festen Funktionen interpretieren, deren Position auf der Ordinate log von und abhängt. Aus dieser Verschiebung entlang der Achse kann man auf die spektrale Empfindlichkeit der retinalen Reaktionssysteme zurückschließen. Es ergeben sich für die drei Reaktionsmechanismen verschiedene Weber-Brüche und nicht, wie von von Helmholtz postuliert, gleiche.
Aufgrund dieser Beobachtungen postuliert Stiles (1946) folgendes Linienelement:
wobei für den hier untersuchten Beobachter 
, 
und 
gilt. Diese Konstanten sind proportional zu den Weber-Brüchen der drei Reaktionssysteme bei hohen Leuchtdichten, d.h. dem Quotienten aus ebenmerklicher Helligkeitsänderung und Helligkeit des Hintergrunds. Mit diesen Werten können die empirisch bestimmten Funktionen 
, 
und 
(die den Kehrwert der empirisch bestimmten Wahrnehmbarkeitsschwelle für Inkremente bei den drei Farbmechanismen R, G, B bezeichnen) näherungsweise folgendermaßen berechnet werden:
Zwischen den Zapfenreaktionen R, G, B und den CIE-1931-Farbwerten nimmt Stiles (1920) folgenden linearen Zusammenhang an, der den spektralen Empfindlichkeitsfunktionen mit einem Maximum bei 580, 540 bzw. 445 nm entspricht:
Bei hohen Leuchtdichten reduziert sich das in Gleichung 8 definierte Linienelement zu folgender einfacher Form, die dem von Helmholtzschen Linienelement in Gleichung 7 sehr ähnlich ist:
Dieses Linienelement sagt einige experimentelle Beobachtungen gut vorher, beispielsweise ebenmerkliche Wellenlängenunterschiede, spektrale Hellempfindlichkeiten und Farbunterschiedsschwellen in Form von MacAdam-Ellipsen; allerdings existieren auch experimentelle Befunde, die dieses Linienelement nicht erklären kann:
Die spektrale Hellempfindlichkeitsfunktion läßt sich mit Hilfe der Linienelemente auf die folgende Weise bestimmen: Man geht von Paaren monochromatischer Reize aus, die sich in ihrem Farbton ebenmerklich unterscheiden. Dann wird die Leuchtdichte des einen Reizes vom Betrachter so verändert, daß dieser die beiden Reize für maximal ähnlich hält. Dieses Vorgehen wird für verschiedene Reizpaare entlang des sichtbaren Spektrums wiederholt. Sei S = R + G + B, dann gilt für die Farbwertanteile (r, g, b) und (r', g', b') der beiden monochromatischen Reize
und analog für g, g', b und b'. Das Linienelement berechnet sich dann folgendermaßen:
Durch Variieren von S' bei Konstanthalten von r', g', b' wird die Leuchtdichte des entsprechenden Reizes variiert, ohne daß sich dabei dessen Farbton verändert. Nach mehreren Umformungen und Vereinfachungen gelangt man aus diesem Linienelement zur spektralen Hellempfindlichkeitsfunktion
wobei c eine Normierungskonstante ist, die dazu dient, daß bei 555 nm den Wert Eins annimmt, und 
die Farbwertkurven bezeichnen.
Die auf diese Weise berechnete Hellempfindlichkeitskurve stimmt mit der empirisch gemessenen relativ gut überein, nur im kurzwelligen (blauen) Bereich nimmt die theoretische Kurve höhere Werte als die empirische an. Eine mögliche Erklärung sehen Wyszecki und Stiles (1982) darin, daß bezüglich der Helligkeit keine Additivität vorliegt, d.h. die Leuchtdichte der Mischung zweier (monochromatischer) Reize entspricht nicht der Summe der beiden einzelnen Leuchtdichten (eine ausführliche Darstellung hierzu findet sich im Kapitel 5.8.2. von Wyszecki und Stiles, 1982).
Aus dem im vorigen Abschnitt beschriebenen Linienelement läßt sich auch die Unterschiedsschwelle für monochromatische Reize unterschiedlicher Wellenlänge (kurz als Farbtongrenze oder hue limen bezeichnet) berechnen; hierfür verwendet Stiles (1946) folgende etwas unhandliche Formel:
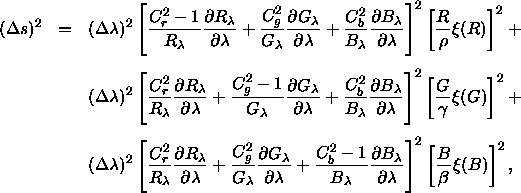
wobei für 
gilt
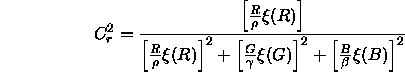
und Analoges für 
und 
.
Die von diesen Linienelementen vorhergesagten ebenmerklichen Wellenlängenunterschiede sind proportional zu den empirisch bestimmten, nur im kurzwelligen Bereich sind die vorhergesagten Werte etwas zu niedrig, wie in Abbildung 3 zu sehen ist. Dies kann daran liegen, daß bei der experimentellen Bestimmung der Unterscheidbarkeit monochromatischer Reize höhere Intensitäten (bis zur zwanzigfachen) verwendet werden mußten, während bei den Vorhersagen durch das Linienelement von konstanter Helligkeit ausgegangen wird.
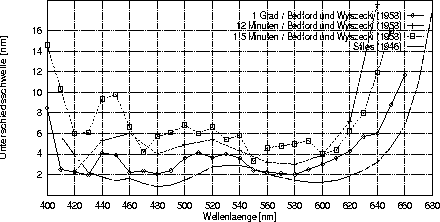
Abbildung:
Theoretische und empirische Unterschiedsschwelle für Spektralfarben:
In dieser Abbildung sind nochmals durch Punkte gekenzeichnet die Schwellen für Farbunterschiede der Versuchsperson GW von Bedford und Wyszecki (1958) für verschiedene Reizgrößen eingezeichnet. Die eng gepunktete Linie stellt die vom Linienelement nach Stiles (1946) vorhergesagten Unterschiedsschwellen dar; die Werte wurden aus der Tabelle 1 von Stiles (1946) entnommen.
Die Unterscheidbarkeit von beliebigen Farben in der Normfarbtafel läßt sich durch Linienelemente vorhersagen, wenn man deren Helligkeit konstant hält; gleiche Helligkeit bedeutet hier, daß die gleiche Anzahl an Photonen absorbiert werden muß, wie Trabka (1968a) zeigt. Zur Bestimmung der Farbwerte (R, G, B) im Rezeptorraum wendet Stiles (1946) die Transformation aus Gleichung(9 für die Normfarbwertanteile an. Aus den Farbkoordinaten in der Normfarbtafel lassen sich so bei konstanter Leuchtdichte die Unterschiedsschwellen für die einzelnen Primärreize bestimmen als
wobei die 
die Einträge der obigen Transformationsmatrix bezeichnen und für 
und 
analoge Beziehungen angenommen werden. Für das vollständige Linienelement gilt dann
wobei hier folgende Ersetzungen gelten:
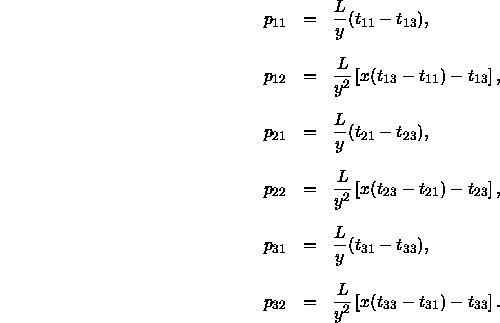
Die so berechneten Linienelemente besitzen eine quadratische Form, die verwendet werden kann, um Unterscheidbarkeits-Ellipsen in der Normfarbtafel einzuzeichnen. Stiles (1946) erhält Ellipsen, die in Abbildung 4 zu sehen sind, mit ähnlicher Orientierung wie diejenigen von MacAdam (1942), allerdings sind sie zwanzigfach größer; ihre Fläche ist jedoch etwa zur Fläche der entsprechenden Ellipsen bei MacAdam (1942) proportional.
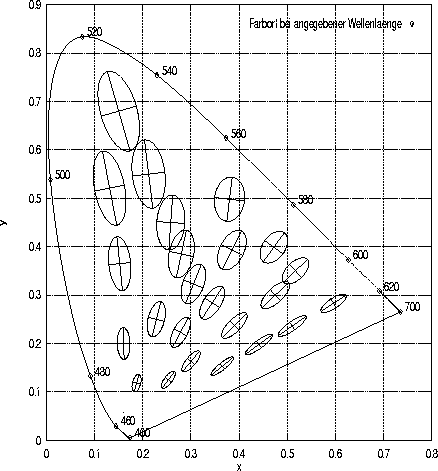
Abbildung 4:
Diskriminationsellipsoide nach Stiles (1946):
In dieser Abbildung sind die von Stiles (1946) berechneten Diskriminationsellipsen (in dreifacher Vergrößerung) sowie deren Hauptachsen zu sehen. Für die Zeichnung wurden die von Stiles (1946) in der Tabelle 2 angebenen Parameter verwendet.
Im vorigen Abschnitt wurde festgestellt, daß sich die vom Linienelement geschätzten Diskriminations-Ellipsoide von den empirisch von MacAdam (1942) bestimmten unterscheiden. Dieser Unterschied läßt sich anhand der Gaußschen Krümmung spezifizieren: Die Diskriminationsellipsen von Reizen mit den Koordinaten (x, y) in der Normfarbtafel (bei kontanter Leuchtdichte) können durch ein Linienelement eines zweidimensionalen Riemannschen Raums beschrieben werden:
Außerdem sei g die Determinante der Transformationsmatrix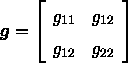 
. Wird ein zweidimensionaler Riemannscher Raum auf einen beliebigen dreidimensionalen Raum abgebildet, entsteht eine Oberfläche mit der Gaußschen Krümmung K, die sich aus dem Linienelement folgendermaßen bestimmen läßt:
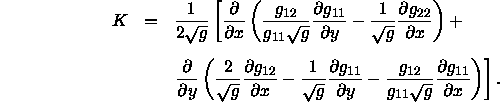
Wie man sieht, hängt die Gaußsche Krümmung nur vom Farbort (x,y) und der Transformationsmatrix 
ab. Wendet man diese Gleichung auf die Berechnung des Linienelements nach Gleichung 10 an, findet man zwar eine Abhängigkeit der Krümmung K vom Farbort (x,y), aber man erhält für positive Farkoordinaten immer eine negative Krümmung. Stiles (1946) leitet im Anhang seiner Arbeit folgende etwas einfachere Formel zur approximativen Bestimmung der Gaußschen Krümmung des Farbraums am Ort (R, G, B) her:
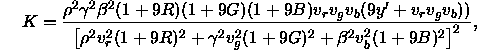
wobei 
als konstant angenommen wird und er folgende weiteren Konstanten berechnet:
Wichtig an den hier dargestellten Überlegungen zur Gaußschen Krümmung des Farbraumes ist nun, daß der Term 
wegen des negativen Wertes von 
immer negativ ist und somit auch die aufgrund des Linienelements vorhergesagte Gaußsche Krümmung K (ebenso wie die von Wyszecki und Stiles berechnete Gaußsche Krümmung). Die aus den empirischen Daten von MacAdam (1942) bestimmte Gaußsche Krümmung ist dagegen manchmal positiv und manchmal negativ. Es läßt sich also prinzipiell keine Transformation finden, die die empirische und die aus dem Linienelement vorhergesagten Oberflächen gleichen Farbabstandes ineinander überführen (siehe hierzu auch Wyszecki & Stiles, 1982).
Die Riemannschen Oberflächen, die entweder aus dem Linienelement oder aus den MacAdam-Ellipsen bestimmt werden können, lassen sich in einen dreidimensionalen euklidischen Raum einbetten. Auf einer solchen Oberfläche wird jede Ellipse zu einem Kreis mit gleichem Radius; man gelangt so zu einem Oberfläche gleichen Farbabstands (uniform-chromaticity-scale surface). Wenn 
die kartesischen Koordinaten im euklidischen Raum bezeichnen, dann repräsentiert das Linienelement den quadrierten Abstand zwischen zwei nebeneinander liegenden Punkten auf der Oberfläche. Betrachtet man die kartesischen Koordinaten als Funktion des Farbortes (x,y), also
dann lautet die Formel für das Linienelement
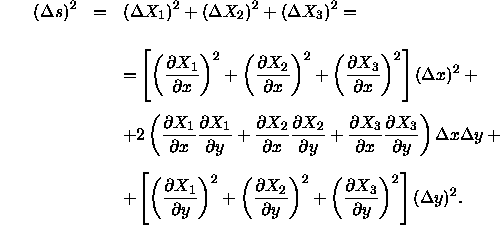
Wyszecki und Stiles (1982, S. 668 f.) geben für die Bestimmung der metrischen Koeffizienten folgende Formeln an:
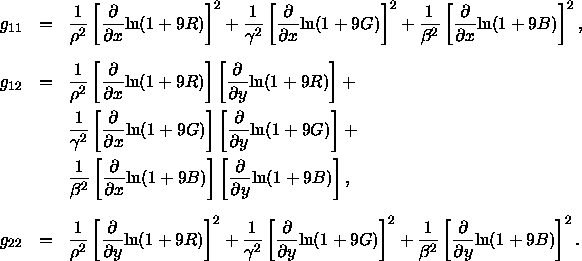
Vergleicht man die beiden letzten Gleichungen, erkent man den Mechanismus der Funktionen 
:
Durch Bilden des Anti-Logarithmus erhält man daraus
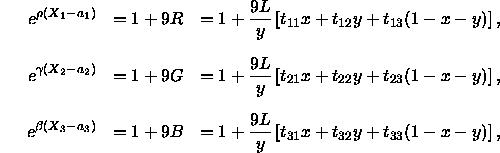
Schließlich erhält man durch Eliminieren von x und y aus diesen Gleichungen die Formel für die Oberfläche der gleichförmigen Farbabstandsskala:
wobei
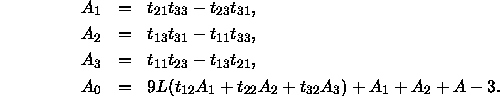
Bereits am Anfang dieses Kapitels wurde die auf Schrödinger (1920) zurückgehende Idee aufgegriffen, Konturen gleichen Farbtons und gleicher Buntheit aus dem Linienelement abzuleiten: Auf einer Oberfläche konstanter Helligkeit bezeichnen die Orte konstanten Farbtons geodätische Linien, die alle an einem Punkt starten, der einem achromatischem Reiz der selben Helligkeit entspricht, und am Spektralzug enden. Orte konstanter Buntheit sind geodätische Kreise um den ``achromatischen'' Punkt herum. Die Berechnung dieser Linien und Kreise ist sehr unhandlich und wird von Wyszecki und Stiles (1982, S. 670 ff.) beschrieben.
Trabka (1968a, 1968b) wendet die Konzepte der Signalentdeckungstheorie auf das Linienelement von Stiles (1946) an. Er betrachtet die einzelnen Zapfen als nicht-ideale Empfänger von elektromagnetischen Schwingungen; alle Rezeptoren eines Typs zusammen werden als ein Detektor-Mechanismus betrachtet. Den Signal-Rausch-Abstand (Signal-to-Noise Output) der drei Rezeptortypen bestimmt Trabka (1968a) nach folgender Formel:
wobei folgende Definitionen gelten:
; genau genommen müßte man deshalb 
schreiben, da der konkrete Wert von m wellenlängenabhängig ist.
bezeichnet den Unterschied zwischen den beiden zu vergleichenden Reizen;
bezeichnet die Totzeit der Rezeptoren in Millisekunden, also diejenige Zeitspanne nach der Absorption eines Photons, in der die Absorption eines weiteren Photons den Rezeptoroutput nicht weiter verändert. Trabka (1968b) empfiehlt, hierfür einen Wert von 7 Millisekunden einzusetzen.
der Augen und von der ``Auszeit'' abhängen:
Nun nimmt Trabka (1968a) an, daß bei zunehmendem Signal-Rausch-Abstand auch die Veränderung des Outputs der Detektor-Mechanismen und somit der wahrgenommene Abstand zwischen den beiden Reizen zunimmt. Für diesen Abstand definiert er für ein System aus N verschiedenen Empfängern folgendes Linienelement:
Hierbei bezeichnet 
eine Skalierungskonstante. Das Linienelement ist also eine Summe des Signal-Rausch-Abstands am Output von verschiedenen Rezeptoren, die sich nur in ihrer spektralen Absorptionsfunktion 
und in ihrem Verstärkungsmechanismus 
unterscheiden. Trabka (1968a) zeigt, daß die Werte für diese Verstärkungsmechanismen den Faktoren 
im Linienelement von Stiles (1946) entsprechen. Die Weber-Brüche 
sind damit umgekehrt proportional zur Wurzel aus der Quantenausbeute der Vestärkungsmechanismen.
Wie von Trabka (1968a) gezeigt wird, impliziert Konstanthalten der Helligkeit, daß 
gelten muß. Gilt hingegen, daß 
konstant ist, dann liegt ein konstanter Farbton vor.
Trabka (1968a) weist auch auf den Zusammenhang zwischen dem Nenner in Gleichung 13 und den Funktionen 
von Stiles (1946) hin. Letzterer nennt folgenden empirischen Zusammenhang für 
:
wobei er für a = 1, b=0.3 und c = 0.0125 empfiehlt. Trabka (1968a) zeigt, daß seine Version des Linienelements zu beinahe identischen Vorhersagen kommt wie die Formulierung von Stiles (1946). Er zeigt außerdem, daß sich auf diese Weise die spektrale Hellempfindlichkeitsfunktion und die Unterscheidbarkeitsschwelle für Farbtonunterschiede sowohl von normalen Trichromaten als auch von Dichromaten gut vorhersagen lassen; würde man dagegen einen idealen Detektor postulieren, würden sich für Dichromaten abweichende Vorhersagen ergeben.
Von Vos und Walraven (1972a, 1972b) stammt die komplexeste Linienelement-Theorie. Sie basiert auf der Quantennatur des Lichts und gilt für foveales Sehen von 2 großen Feldern. Im Rahmen dieser Erläuterungen bezeichnet R, G und B die Anzahl der vom entsprechenden Zapfentyp absorbierten Photonen. Dieser Theorie liegen folgende Annahmen zugrunde:
Zuerst werden Reize niedriger Leuchtdichte betrachtet: Der Signal-Rausch-Abstand des Outputs der Zapfen eines Typs kann für 
betrachtet werden als 
, wobei 
die durchschnittliche Anzahl der innerhalb einer Sekunde vom Rezeptortyp i absorbierten Quanten angibt. Unter der Annahme, daß die gemeinsame Reaktion der drei Zapfenmechanismen R, G, B gleich der Wurzel aus der Summe der quadrierten einzelnen Zapfenreaktionen ist, erhält man folgende Formel für das physikalische Linienelement:
wobei R, G, B die Reaktionen der drei unabhängig voneinander arbeitenden Mechanismen sind, die sich über Lineartransformationen aus den CIE-1931-Spektralwertkurven berechnen lassen. Dieses Linienelement zeigt eine gewisse Ähnlichkeit zu demjenigen von Schrödinger, das jedoch die drei Komponenten noch entsprechend der Leuchtdichte gewichtet und so das Webersche Gesetz berücksichtigt. Dies ist bei dem Modell von Vos und Walraven (1972a) nicht der Fall: Der Weber-Bruch ist hier nicht konstant, sondern erhöht sich mit der Wurzel der Leuchtdichte, was im Bereich der absoluten Schwelle auch durchaus sinnvoll ist.
Im Modell von Vos und Walraven (1972a) werden jedoch nun nicht die Reaktionen der Zapfentypen wie in Gleichung 14 angegeben betrachtet, sondern drei aus diesen generierte Gegenfarb-Signale, die folgendermaßen bestimmt werden:
Diese drei Farbsignale werden dann zusammen mit Gewichtungsfaktoren 
der Farbkanäle (die das Adaptationsniveau charakterisieren) sowie den Standardabweichungen 
der internen Schwankungen in den L, F, S-Signalen zur Berechnung des physiologischen Linienelements eingesetzt:
Vos und Walraven (1972b) zeigen, wie man die Faktoren ebenfalls durch die Rezeptorerregung R, G, B ausdrücken kann (siehe unten). Sie nehmen nun an, daß das gemeinsame Output-Signal direkt proportional zum ebenmerklichen Farbunterschied zweier Reize ist. Dieses Linienelement läßt sich nach Vos und Walraven (1972b) auch so umrechnen, daß nur die Zapfenreaktionen R, G, B als Variablen darin vorkommen. Nach Umformen erhält man dann:
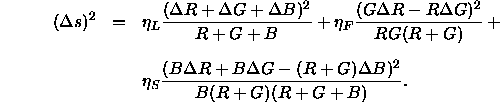
Setzt man die Leuchtdichte L = R+G+B und die Farbwertanteile r = R/L sowie g = G/L und b = B/L, dann erhält man nach Umformen folgende Gleichung für das Linienelement:
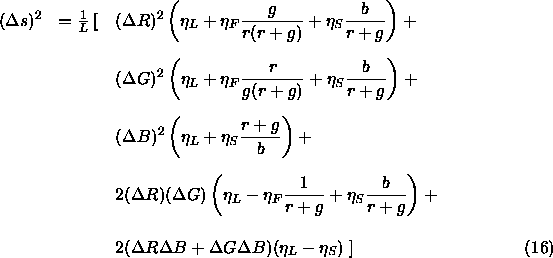
Dieses Linienelement ist komplexer als die bisher vorgestellten, da hier nun auch die Kreuzprodukte der Farbkanäle einbezogen sind. Dadurch müssen die Ellipsen, die die Farbdiskrimination beschreiben, nicht mehr entlang der R, G, B-Achsen orientiert sein. Setzt man alle drei Gewichtungsfaktoren 
, dann reduziert sich diese Gleichung zur Gleichung 14, die die Reaktion der drei Zapfentypen im Bereich der absoluten Schwelle - in dem die drei Zapfentypen unabhängig voneinander reagieren - beschreibt.
Das bisher geschilderte Modell gilt, wie bereits erwähnt, nur für niedrige Leuchtdichten. Um es auch bei mittleren und hohen Leuchtdichten anwendbar zu machen, führen Vos und Walraven (1972b) das Sättigungs-Modell und das Hypersaturierungs-Modell ein:
Sättigung eines Farbkanals 
tritt dann auf, wenn die neuronale Entladungsfrequenz so hoch ist, daß sie nicht mehr gesteigert werden kann, weil auf jedes Feuern des Neurons eine gewisse Refraktärzeit folgt, wie Trabka (1968a) annimmt. Die Anzahl der Entladungen 
hängt dann von der Anzahl eintreffender Photonen n folgendermaßen ab:
wobei 
diejenige Photonenzahl bezeichnet, ab der das Phänomen der Sättigung auftritt. Vos und Walraven (1972b) führen darüber hinaus noch das Konzept der neuronalen Genauigkeitsreduzierung (accuracy reduction) 
ein, das ein Nachlassen der Genauigkeit der Information über die Anzahl der Photonen postuliert, wenn die Grenze erreicht wird; der postulierte numerische Zusammenhang lautet
Bei hohen Leuchtdichten wird proportional zu n; dadurch wird das Linienelement aus Gleichung 16 dem von Helmholtzschen ähnlich, das ja für höhere Leuchtdichten Webersches Verhalten vorhersagt.
Vos und Walraven (1972b) elaborieren das Sättigungsmodell noch weiter, indem sie zusätzlich berücksichtigen, daß die oben genannte Refraktärzeit 
, in der das Neuron nicht feuern kann, selbst gewissen Schwankungen 
unterliegt. Diese Ungenauigkeit führt dazu, daß sich geringe Unterschiede der Entladungsfrequenz nicht interpretieren lassen, sobald das Phänomen der Zapfensättigung auftritt; diese zusätzliche Behinderung des Informationsflusses nennen sie Übersättigung. Die Autoren modifizieren dazu die Gleichung 18 für folgendermaßen:
In dieser Gleichung bezeichnet 
die Anzahl an Quanten, für die Übersättigung auftritt; das Verhältnis von zu hängt nicht von der Zapfenart ab und lautet
Wie Vos und Walraven (1972b) zeigen, hängen die numerischen Werte für die Sättigung eng mit denen für die Hypersaturierung zusammen.
Auf der Grundlage der in den vorherigen Abschnitten beschriebenen Modifikationen gelangen Vos und Walraven (1972b) nun zu einem allgemeinen Modell des Linienelements. Zuerst werden die Zapfensignale addiert, wobei gilt L = R+G+B und Y = R+G. Anschließend sättigen diese Signale entsprechend der Gleichung 17; die Genauigkeit der Weiterleitung dieser Signale wird zuerst durch die Poisson-Statistik beeinflußt und anschließend wirken sich Sättigung und Übersättigung entsprechend Gleichung 19 aus, so daß für die Genauigkeit gilt:
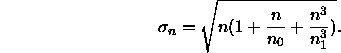
Daraus entwickeln Vos und Walraven (1972b) das von ihnen als physikalisches Linienelement bezeichnete Modell, indem sie 
durch dividieren und den Term quadrieren:
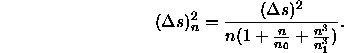
Die Signale der beiden Gegenfarbmechanismen werden als 
und als 
bestimmt. Aus diesen Bausteinen läßt sich nun schließlich die Formel für das Linienelement angeben, das durch die Rezeptorsignale R, G, B zustandekommt:
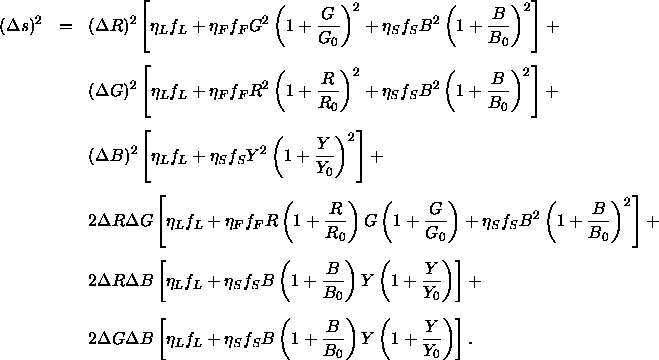
Hierbei sind 
folgendermaßen definiert:
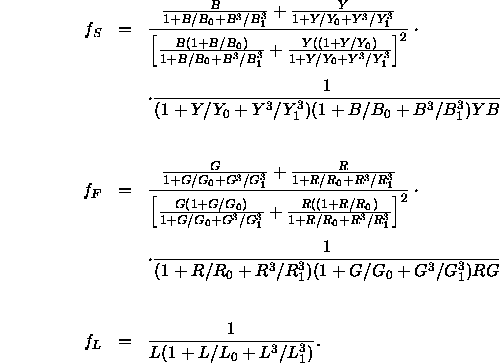
Mit diesem Modell lassen sich Daten zur Farbdiskrimination recht gut vorhersagen, sowohl was die Wellenlängen-Diskrimination betrifft als auch bezüglich der Farbton-Unterscheidbarkeit.
Die bisher in diesem Kapitel beschriebenen theoretisch hergeleiteten Linienelemente von Helmholtz (1891), Schrödinger (1920), Stiles (1946), Trabka (1968a, 1968b) und Vos und Walraven (1972a, 1972b) kommen zwar mit relativ wenigen Annahmen aus, sie können aber nicht alle empirischen Befunde erklären; die empirischen Linienelemente, beispielsweise die von MacAdam (1942b), machen dagegen keine Annahmen über die der Farbunterscheidbarkeit zugrundeliegenden Mechanismen. Wyszecki und Stiles (1982) nennen folgende Grundannahmen zur Bestimmung solcher Linienelemente, die sie als induktive bezeichnen:
Unter diesen Annahmen läßt sich die quantitative Reaktion des i-ten Mechanismus auf eine Reiz mit bestimmter spektraler Strahlungsverteilung als Funktion 
von dessen Farbwerten repräsentieren. Die Reaktionsdifferenz bei geringfügig unterschiedlichen Reizen (R, G, B) und (R', G', B') läßt sich durch die Taylor-Expansion ausdrücken als
wobei
Falls sich die Mechanismen der Farbwahrnehmung hinreichend stark unterscheiden, läßt sich auch die Reaktionsdifferenz untersuchen, wenn nur ein einziger der Mechanismen reagiert; dann könnte man für die Reaktion einfach den Wert der Funktion 
einsetzen. Zwei Reize können im einfachsten Fall als unterschiedlich empfunden werden, wenn der Betrag von über einer Schwelle 
liegt. Dieser Schwellenwert hängt im allgemeinen wiederum vom durchschnittlichen Erregungsniveau ab (also 
) und möglicherweise auch vom Reaktionsniveau der anderen Mechanismen:
Trennbarkeit der Mechanismen würde bedeuten, daß man zur Untersuchung des i-ten Mechanismus alle anderen Mechanismen blockieren könnte, ohne deren Einfluß auf die Schwelle 
zu verändern.
Man kann aber auch von probabilistischen Schwellen ausgehen, wobei dann 
die Wahrscheinlichkeit bezeichnet, daß durch den Mechanismus i einen Reizunterschied wahrgenommen wird. Um Unabhängigkeit der Entdeckenswahrscheinlichkeit vom momentanen Erregungsniveau zu gewährleisten, führen Wyszecki und Stiles (1982) folgende Wahrscheinlichkeit ein:
Man erhält so für alle Reaktionsniveaus eine Wahrscheinlichkeit von 0.5 dafür, daß der Reaktionsunterschied genau der Schwelle entspricht. Wenn die Wahrscheinlichkeiten für das Entdecken eines Unterschiedes für die einzelnen Mechanismen unabhängig voneinander sind, dann ergibt sich bei n Mechanismen die Wahrscheinlichkeit dafür, daß mindestens einer davon den Unterschied bemerkt, als
Insgesamt ist die Diskriminationsschwelle erreicht, wenn 
. Wenn die quantitativen Eigenschaften der Mechanismen durch die Funktionen , 
und 
genau bestimmt sind, dann lassen sich die Reaktionsdifferenzen 
berechnen, die einem wahrnehmbaren Farbunterschied entsprechen. Definiert man
dann gilt für die Diskriminationsschwelle
Ist 
im Vergleich zu allen anderen relativ groß, dann hat diese Gleichung folgende Lösung, weil 
monoton von abhängt:
wobei 
und 
sehr klein sind und sogar verschwinden, wenn das Verhältnis 
gegen Null geht. Aus der sogenannten Quadratsummen-Relation
folgt eine der Gleichung 20 ähnliche Beziehung:
Diese Ähnlichkeit wird von Wyszecki und Stiles (1982) deshalb herausgestellt, weil damit gezeigt ist, daß für den Spezialfall von einem großen und ansonsten kleinen die Lösung der Quadratsummen-Gleichung 22 einen guten Näherungswert für die Lösung der Gleichung 20 für die strenge Schwellentheorie liefert. In vielen Theorien wird deshalb die Quadratsumme als eine im Schwellenbereich gültige Näherung betrachtet. Die Unterschiede zwischen den exakten aus Gleichung 20 berechneten Schwellen und den aus Gleichung 21 approximativ bestimmten hängen von der Gestalt der Wahrscheinlichkeitsfunktion 
ab.
Zur Bestimmung dieser Wahrscheinlichkeitsfunktionen aus empirischen Kurven zur Entdeckungswahrscheinlichkeit verweisen Wyszecki und Stiles (1982) auf die allgemeinen Farbgrenzen (general color limens), die beispielsweise von MacAdam (1942b) verwendet werden: Dabei werden die Farbwerte des einen Reizes bei (R, G, B) fixiert und diejenigen 
des anderen Reizes können im 
-Farbraum entlang einer Linie, auf der der erstere Reiz liegt, variieren. Das Verhältnis 
bleibt konstant, auch wenn sich deren absoluter Wert ändert; es gilt somit
wobei l, m und s den Cosinus der Richtung der Gerade zur jeweiligen Achse bezeichnen, auf der der variable Reiz wandern kann, und s die Distanz zum festen Reiz auf dieser Gerade ist. Dann läßt sich die Wahrscheinlichkeit dafür, daß ein Unterschied entdeckt wird, berechnen als
wobei S der Schwellenwert von s sein soll. Ist die Schwelle S gleich dem Abstand s, erhält man P=0.5. Der Verlauf der Wahrscheinlichkeitsfunktion läßt sich damit experimentell für verschiedene Reize (R, G, B) und Richtungen (l, m, n) bestimmen. Der exakte Verlauf ist gegeben durch
wobei die Funktion E den Fehler bezeichnet:
Es zeigt sich, daß keine nennenswerte Abhängigkeit dieser Funktionen von dem Primärreiztripel oder dem Erregungsniveau besteht.
Wyszecki und Stiles (1982) zeigen für den Fall von zwei Mechanismen zum Farbensehen, daß die Vorhersagen durch die einfacheren Quadratsummen (nach Gleichung 21) den exakten Vorhersagen nach Gleichung 20 gut entsprechen, wenn die Steigung der Wahrscheinlichkeitsfunktionen bei 2.56 liegt. Bei geeignetem Steigungsparameter gilt dies auch für mehr als zwei Mechanismen, wenn deren Wahrscheinlichkeitsfunktion die selbe Gestalt hat. Empirisch ermittelte Steigungsparameter erweisen sich jedoch im allgemeinen als etwas zu steil und manchmal sogar als viel zu steil.
Im einfachsten Fall hängt die Reaktion eines Farbmechanismus nur von einem einzigen Farbwert ab; ist dies R, dann gilt
und
Nimmt man außerdem an, daß die Unterscheidbarkeitsschwelle ebenfalls nur vom selben Mechanismus abhängt, dann gilt 
. Ein derartiger Mechanismus - man nennt ihn auch (einfachen) Klasse-I-Mechanismus - trägt zur Quadratsumme auf folgende Weise bei:
Für das eigentliche Unterscheidungsvermögen ist aber nur das Verhältnis 
verantwortlich. Diese Funktion 
kann je nach zugrunde gelegtem physiologischen Modell auf verschiedene Weise zustande kommen:
:
:
folgendem Zusammenhang unterliegt:
Auf diese verschiedenen Arten kann der Term 
im Linienelement zustande kommen. Wirken drei solcher völlig unabhängiger einfacher Mechanismen, berechnet sich das Linienelement folgendermaßen:
Die Hauptachsen der daraus resultierenden Diskriminationsellipsoide sind parallel zu den Koordinatenachsen und ihre Länge in Richtung einer Achse ist die selbe für alle Reize mit gleichem Farbwert auf der entsprechenden Achse. Die Modelle von von Helmholtz (1891), Schrödinger (1920) und Stiles (1946) sind von dieser Art. Sie lassen sich aus einem physiologischen Modell mit folgenden Reaktionskurven ableiten:
mit konstanten Schwellen 
, 
und 
, so daß als Schwelle für einen Unterschied gilt:
mit 
reellen positiven Konstanten. Diese Gleichung entspricht (bis auf die Formulierung) dem Stilesschen Linienelement in Gleichung 8. In den hier eingeführten Begriffen läßt sich das Schrödingersche Linienelement formulieren als
Hier hängen die einzelnen Terme zwar auch nur von jeweils einem Mechanismus ab, aber die Schwellenwerte werden durch alle drei Erregungsniveaus bestimmt; solche Mechanismen bezeichnet man als (komplexe) Klasse I-Mechanismen. Zu dem Modell von Schrödinger (1920) kann man auf zwei Arten gelangen:
muß vor einem Hintergrundrauschen entdeckt werden, das vor allem vom Erregungsniveau des i-ten Mechanismus abhängt, aber auch mit der Erregung der anderen Mechanismen zunimmt.
Die Reaktion der Klasse-II- und Klasse-III-Mechanismen hängt von zwei bzw. drei Farbwerten ab; dies kann an Rezeptoren, die mehr als einen Farbstoff besitzen, liegen oder daran, daß auf neuronaler Ebene mehrere Rezeptortypen interagieren:
wobei die Leuchtdichte 
von den Konstanten 
und 
abhängt (diese Faktoren werden für nicht zu intensive Reize deshalb als konstant angenommen, weil keine Bleichung erwartet wird). Der Schwellenwert ist ebenfalls von der Leuchtdichte abhängig.
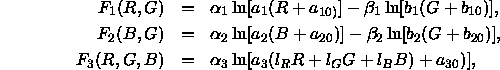
und es werden konstante Schwellen 
, 
und 
angenommen. Damit gelangt man zu folgendem Linienelement:
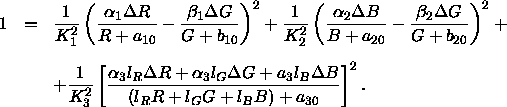
Wird dieses Linienelement auf den Fall von MacAdam (1942) - Diskriminationsellipsen in einer Ebene konstanter Leuchtdichte - angewendet, vereinfacht sich das Linienelement zu 
, wobei die 
die jeweilige Schwelle bezeichnet.
Die in diesem Abschnitt vorgestellten Linienelement-Theorien eignen sich dazu, das Farbdiskriminationsvermögen relativ gut vorherzusagen; sie können auch dazu verwendet werden, einen Farbraum so zu transformieren, daß er zu einem uniform color space wird, d.h. daß gleiche Abstände in diesem Farbraum auch gleiche Farbunterschiede bezeichnen.
Es ist jedoch kritisch anzumerken, daß diese Linienelement-Theorien nur für genau spezifizierte Bedingungen analysiert wurden. Meist handelt es sich dabei um foveales Sehen bei mittlerer Leuchtdichte, das durch den Simultanvergleich zweier Reize untersucht wird; nur das Modell von Vos und Walraven (1972b) versucht, den gesamten Bereich verschiedener Leuchtdichten zu erfassen. Die Bestimmung der Unterscheidbarkeit von Farben gleicher Helligkeit wird meist nur für monochromatische Reize bestimmt (dies müßte jedoch nicht prinzipiell so sein).
Wandell (1985) weist darauf hin, daß die metrischen Koeffizienten des Linienelements abhängig seien vom Adaptationszustand des Auges; nur aufgrund unterschiedlicher Adaptationszustände dürften deshalb Nichtlinearitäten auftreten. Wenn man dagegen den Adaptationszustand genau kontrolliert (bzw. konstant hält), dann läßt sich die Unterscheidbarkeit zweier Reize alleine aus der Differenz der die beiden Reize repräsentierenden Vektoren bestimmen. Wandell (1982, 1985) bezeichnet diese Überlegung als Vektordifferenz-Hypothese und betrachtet sie als Spezialfall des Linienelements.
Trifft dieses Modell zu, so könnte man das Linienelement doch zur Beschreibung von Adaptationseffekten verwenden: Man müßte dann eine Transformationsvorschrift finden, die die metrischen Koeffizieneten, die vom Adaptationskontext abhängen, vom Ausgangskontext auf den Zielkontext abbildet.
Zur Vorhersage der Befunde in dem hier durchgeführten Experiment sind die Linienelement-Theorien nur bedingt geeignet, da sie zum einen keine Aussagen über mögliche Auswirkungen der Gedächtnismethode machen und da außerdem die Kontextabhängigkeit des Farbensehens nicht von diesen Theorien berücksichtigt wird. Es kann lediglich versucht werden, zu überprüfen, inwieweit die aus den Daten von meinem Experiment bestimmten Diskriminationsellipsen mit denen übereinstimmen, die die Linienelement-Theorien vorhersagen.
zurück zur Hauptseite (Theorien der Farbwahrnehmung)
zurück zu meiner homepage
Anmerkungen und Mitteilungen an
rainer@zwisler.de
