Einführende Beispiele

MDS-Skalierung kann in sehr unterschiedlichen Bereichen eingesetzt werden. Einige Beispiele hierfür sind folgende:

• Anthropologie (Vergleich kultureller Gruppen aufgrund von deren Überzeugungen, Sprache und Artefakten);
• Erziehungswissenschaften (Struktur der Intelligenz, verschiedener Testbatterien und der Klassenzimmer-Umgebung);
• Marktforschung (Konsumentenverhalten bezüglich unterschiedlichster Produkte);
• Psychologie (Wahrnehmung und Evaluation von visuellen, auditiven und sozialen Einheiten);
• Soziologie (Bestimmung der Struktur von Gruppen und Organisationen aufgrund von Wahrnehmungen und Interaktionen).

Dabei kann die MDS zur Bestimmung und Interpretation der Dimensionalität, die den Ähnlichkeitsurteilen zugrunde liegt, eingesetzt werden, zur Datenreduktion und zur Bestätigung von Konfigurationshypothesen. Meist soll die kognitive Struktur (oder ``perceptual map''), die Ähnlichkeitsurteilen und damit allgemein der Wahrnehmung entsprechender Objekte zugrunde liegt, ermittelt werden. Folgende Beispiele aus unterschiedlichen Bereichen lassen sich nennen:

Werbung: In einer Untersuchung konnten sechs verschiedene Arten von gutem Aussehen unterschieden werden sowie für jede Kategorie repräsentative Modelle gefunden werden. Eine weitere MDS führte zu acht verschiedenen Typen von Schönheiten (classic beauty, cute, sex kitten, sensual, girl-next-door, exotic, feminine, trendy), denen verschiedene Arten von Parfum und Frauenzeitschriften zugeordnet werden können.

Konsumentenverhalten: Durch eine MDS wurde der Zusammenhang zwischen Kaufverhalten und Erfahrung mit einem bestimmten Produkt ermittelt: Manche Produkte werden eher wegen ihres Nutzens gekauft, andere aus ästhetischen Gründen. Daraus lassen sich geeignete Vermarktungsstrategien ableiten.

Human Ressource-Management: Mit einer konfirmatorischen MDS wurde die Arbeitsunzufriedenheit von Arbeitern untersucht, die die Ähnlichkeit von verschiedenen Verhaltensweisen beurteilen sollten, die Unzufriedenheit mit der Arbeit ausdrücken.

Psychologie: Die MDS läßt sich auch zur Bestimmung derjenigen Dimensionen einsetzen, aufgrund derer zwischen verschiedenen Politikern unterschieden wird.

Tourismus: Eine MDS-Analyse von staatlichen Tourismus-Produkten sollte den Einfluß der entsprechenden Politik verschiedener Bundesstaaten untersuchen. Dadurch läßt sich das Image des entsprechenden Bundesstaates ermitteln.

Konstruktion einer Verhältnis-MDS

Borg (1981) beginnt mit der Konstruktion einer Verhältnis-MDS aus den Entfernungen zwischen zehn Städten: Die Entfernungen zwischen den Orten sollen in einer zweidimensionalen Ebene repräsentiert werden. Dabei ist der Maßstab frei wählbar, da nur Verhältnisse von Distanzen betrachtet werden. Die Proximitäten (Nähewerte) zwischen den Punkten i und j sollen über einen Skalierungsfaktor von der (beispielsweise euklidischen) Distanz zwischen den beiden Punkten abhängen; es soll also gelten

Da der Skalierungsfaktor konstant bleibt, kürzt er sich bei Betrachtung von Verhältnissen von Proximitäten heraus

so daß die MDS-Lösung verhältnisskaliert ist.

Die Orientierung der Konfiguration ergibt sich aus der Wahl der ersten eingezeichneten Punkte (indem man z.B. mit den beiden am weitesten entfernten Städten beginnt). Die so gefundene Lösung ist jedoch nicht eindeutig: Dabei sind zwei Transformationsgruppen denkbar, die die Entfernungen bzw. deren Verhältnis invariant lassen:

Starre Bewegungen (Isometrie, also Transformationen, die die Metrik gleich lassen): Es sollen die (absoluten) Distanzen invariant bleiben, daher sind Rotation, Reflexion und Translation (also Verschiebung) zulässige Transformationen.

Ähnlichkeits-Transformationen sollen Verhältnisse von Distanzen unverändert lassen, was bei Rotation, Reflexion, Translation und Dilatation (zentraler Streckung) der Fall ist.

Konstruktion einer Ordinal-MDS

Man kann die Entfernungen aber auch so durch Distanzen einer Punktekonfiguration repräsentieren, daß nur noch die Rangordnung von Daten und Distanzen übereinstimmt, indem man beispielsweise die Daten durch ihre Rangzahl ersetzt. In diesem Fall sind dann isotone (ordnungserhaltende) Transformationen der Daten zulässig (isometrische Transformationen sind ein Spezialfall von isotonen).

Bei der Konstruktion der ordinalen MDS-Lösung ergeben sich dann für die einzelnen Punkte Lösungen, die im Vergleich zur Verhältnis-MDS wesentlich indeterminierter sind (es sind unendlich viele Lösungen möglich). Allerdings ergibt sich auch bei der ordinalen MDS eine deutliche Reduktion der Freiheit, die einzelnen Punkte an eine bestimmte Stelle zu setzen. Man spricht deshalb hier von einer Lösungsmenge bzw. einem Lösungsraum.

Je mehr Punkte die Konfiguration enthält, desto stärker wird der Lösungsraum eingeschränkt. Es ist sogar möglich, daß der Lösungsraum ``leer'' sein kann, wenn man zuvor einen ungeeigneten Punkt aus der Lösungsmenge der kleineren Konfiguration ausgewählt hat: Es kann sein, daß manche Punkte der Lösungsmenge einer Teilkonfiguration später - bei Hinzunahme eines weiteren Punktes - das größer gewordene System von Ungleichungen nicht mehr erfüllen. Dadurch erweist sich das sukzessive Konstruieren einer MDS-Lösung als problematisch: Mit zunehmendem Umfang der Konfiguration wird es immer schwieriger, überhaupt einen Lösungsraum zu finden, so daß die Konstruktion der Lösung ständig neu begonnen werden muß, indem rückwirkend der Lösungsraum für die ersten betrachteten Punkte immer kleiner wird.

Die Schrumpfung des Lösungsraums bei Erweiterung der Konfiguration liegt daran, daß die Anzahl der Ungleichungen, der ein Punkt der Lösungsmenge unterliegt, sehr viel schneller anwächst als die Zahl der Punkte in der Konfiguration. Borg (1981), zeigt, daß die Anzahl der Ungleichungen u von der Anzahl Punkte in der Konfiguration n folgendermaßen abhängt:

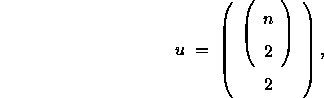
so daß bei 10 Punkten 990 Ungleichungen erfüllt sein müssen, bei 50 Punkten 749.700 und bei 100 Punkten bereits 12.248.775 Ungleichungen. Letztlich sind die einzelnen Punkte der ordinalen MDS-Lösung also auch weitestgehend festgelegt. Vergleicht man die ordinalen mit den metrischen MDS-Lösungen, so findet man eine weitestgehende Übereinstimmung vor. Diese läßt sich damit begründen, daß man nicht von Ordnungsaussagen über Punktepaare ausgeht, sondern über Paare von Punktepaaren, da sich die Ungleichungen auf Distanzen zwischen jeweils zwei Punkten beziehen.

n-dimensionale ordinal-MDS

In diesem Abschnitt wird eine geometrisch-konstruktive Methode dargestellt, mit der man ``auf einen Schlag'' durch ein iteratives Verfahren eine ordinale MDS durchführen kann. Dabei wird von einer Proximitätsmatrix, beispielsweise einer Korrelationsmatrix, ausgegangen und es soll eine Distanzmatrix bestimmt werden, die die Ähnlichkeit zwischen den gemessenen Merkmalen angibt. Im wesentlichen laufen dabei folgende Schritte ab:

1. Man beginnt mit einer zufälligen Startkonfiguration als Distanzmatrix, in der eine entsprechende Zahl an Punkten zufällig plaziert wird, wobei der Abstand eines Punktes zu sich selbst Null beträgt.
2. Jede Zeile dieser Konfiguration wird in dieselbe Rangreihe gebracht wie die entsprechende Zeile der vorgegebenen Proximitätsmatrix: Die Elemente werden in jeder Zeile so permutiert, daß die entstehenden Rangordnungen denen in den Zeilen der Datenmatrix in der gewünschten weise (genauso bei Ähnlichkeiten bzw. umgekehrt bei Unähnlichkeiten) entsprechen. Die so entstandene Matrix bezeichnet man als Rank Image.  
3. Subtrahiert man nun vom Rank Image, das im vorherigen Schritt berechnet wurde, die Distanzmatrix, erhält man eine Korrektur-Matrix, in der die Differenzen zwischen Zieldistanz und tatsächlicher Distanz dargestellt sind. Ein negativer Wert besagt, daß die gemessene Distanz größer war als die Zieldistanz und somit um den entsprechenden Betrag verkleinert werden sollte (und umgekehrt).
4. Nun wird die Distanzmatrix entsprechend der Korrekturmatrix verändert: Für jeden Punkt einzeln findet eine Verschiebung entlang der Verbindungsstrecke zu jedem anderen Punkt statt, deren Betrag und Richtung durch die entsprechende Zelle der Korrekturmatrix gegeben ist.
5. Auf diese Weise erhält man eine neue Distanzmatrix, die eine gegenüber der vorherigen Ausgangskonfiguration verbesserte Konfiguration darstellt. Nun wird mit dieser verbesserten Distanzmatrix wieder der Schritt 2 ausgeführt. Diese iterative Prozedur wird solange wiederholt, bis keine Verschiebung der Punkte mehr stattfindet.

Dieses Verfahren ist aber etwas problematisch, da immer nur zeilenweise entsprechend der Rangplätze permutiert wird: Es kann zu Lösungen (Distanzmatrizen) kommen, die nicht perfekt mit der vorgegebenen Proximitätsmatrix korrespondieren. Um dies zu verhindern, wird das Rank Image so erzeugt, daß die aus der jeweiligen Konfiguration berechneten Distanzen nicht nur innerhalb der Zeilen/Spalten permutiert werden, sondern über alle Zellen der Matrix. Dies wird im folgenden Abschnitt dargestellt.

Intuitive Ableitung der Gradientenmethode

Das im vorigen Abschnitt dargestellte Verfahren ist geometrisch-konstruktiver Art. Durch Einführung eines Koordinatensystems läßt sich die Distanzmatrix aber auch analytisch konstruieren.

Wird bei einer MDS-Analyse nur ein Teil der Beziehungen zwischen den Daten berücksichtigt, dann spricht man von einem konditionalen Vorgehen, da die so erhaltenen Daten nur bedingt aussagekräftig sind. Im letzten Abschnitt wurden beispielsweise nur die zeilenweisen Beziehungen untersucht, so daß es sich um einen zeilen-konditionalen Ansatz handelte. Man kann verschiedene Fälle von Konditionalität konstruieren, indem man gewisse Datenrelationen als irrelevant definiert. Sind dagegen alle Relationen der Datenmatrix von Bedeutung, handelt es sich um unkonditionale Daten. Dieser Fall soll nun dargestellt werden.

Die analytische Bestimmung der Distanzmatrix erfolgt wiederum durch ein iteratives Verfahren, das dem beschriebenen geometrischen Verfahren sehr ähnlich ist:

1. Man geht wieder von einer Zufallskonfiguration der einzelnen Punkte aus. Diese Konfiguration ist aber nun durch die kartesischen Koordinaten der Punkte bestimmt.
2. Aus den Koordinaten der einzelnen Punkte läßt sich die Distanzmatrix der gesamten Konfiguration errechnen. Üblicherweise wird dazu die euklidische Distanz zwischen den Punkten i und j berechnet, deren Formel für den m-dimensionalen Fall lautet  

   

3. Aus der Distanzmatrix wird dann wiederum das Rank Image bestimmt. Dazu werden die Einträge der gesamten Distanzmatrix so permutiert, daß ihre Rangplätze mit denen der Proximitätsmatrix übereinstimmen.
4. Aus dem Rank Image und der Distanzmatrix wird nun die Korrekturfaktor-Matrix berechnet: Man bestimmt, um welchen Faktor eine Distanz verlängert oder verkürzt werden muß. Dazu wird die Differenz zwischen den Einträgen in der Distanzmatrix und den Einträgen im Rank Image bestimmt, also

   

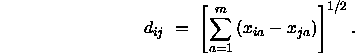
   Die Zahl definiert damit die Richtung und den Betrag des Bewegungsvektors von i nach j. Will man wissen, um welchen Korrekturfaktor eine Distanz verlängert oder verkürzt werden muß, setzt man in Relation zu der gerade betrachteten Distanz :

   

5. Aus der Distanzmatrix und aus den Korrekturfaktoren können jetzt die verbesserten Positionen der Punkte in der Startkonfiguration berechnet werden. Der Korrekturvektor von Punkt i bezüglich j ergibt sich aus der Multiplikation des Vektors von i nach j mit dem Korrekturfaktor . Damit wird beim Übergang von der Konfiguration (t) zu der Konfiguration (t+1) der Punkt i auf der Achse a von nach bewegt durch die Transformation

   

   Man ist aber am Resultat aller Kraftvektoren an i bezüglich der übrigen Punkte in der Konfiguration interessiert. Für die Komponente a führt dies zu der Bewegung

   

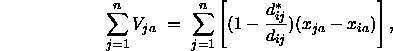
   wobei gesetzt wird und n die Anzahl aller Punkte in der Konfiguration bezeichnet; sei schließlich die Translation von i auf Komponente a relativ zu Punkt j. Für die anderen Komponenten geht man analog vor. Damit errechnet sich die neue Koordinate aus der vorherigen Koordinate folgendermaßen:

    

   wobei die mit t gekennzeichneten Werte aus dem t-ten Iterationszyklus stammen. Die Durchschnittsbildung durch den Faktor ist erforderlich, da sonst der Betrag des Korrekturvektors viel zu groß wäre.

6. Nun hat man also die neuen Koordinaten der Punkte. Solange sich diese deutlich verschieben, wird die iterative Prozedur wiederholt, indem man zum Schritt 2 geht und die gerade berechneten Punkte als neue Startkonfiguration verwendet.

Üblicherweise ergibt sich in den ersten Iterationszyklen die deutlichste Verbesserung der Distanzmatrix. Dies erkennt man bei der Betrachtung der Punktbewegungen in einer grafischen Darstellung. Ein anderes Maß für die Veränderung zwischen zwei Iterationszyklen ist der Zuwachs der Rangkorrelation zwischen Distanzen und vorgegebenen Proximitäten. Meist wird nach wenigen Iterationszyklen keine große Steigerung der Korrelation mehr erzielt.

Man kann aber auch die lineare Korrelation zwischen den Distanzen und den jeweiligen Rank Images untersuchen: Bei perfekten Lösungen müssen die Distanzen mit den Rank Images identisch sein. Dazu kann man sogenannte Image-Diagramme erstellen, in denen für die einzelnen Distanzen die Werte in der Distanzmatrix gegen die Werte im Rank Image angetragen sind. Je besser die Schätzungen werden, desto enger streuen die Punkte um die Winkelhalbierende.

Monotone Regression

 

In diesem Abschnitt wird eine weitere Methode zur Konstruktion einer MDS-Lösung beschrieben. Ausgangspunkt ist wiederum eine Zufallskonfiguration, die in einem Shepard-Diagramm dargestellt ist.

Bei einem Shepard-Diagramm sind auf der Abszisse die Distanzen und auf der Ordinate die Proximitäten für jeden Punkt angegeben. Die Werte auf der Ordinate besitzen nur ordinale Information und es handelt sich um kategoriale Werte, zwischen denen kein diskreter Übergang möglich ist, da sie ja nur Paare von Items bzw. deren Ähnlichkeit repräsentieren. Verbindet man diese Punkte entsprechend der Rangreihe der Proximitäten, erhält man eine aufsteigende Linie. Bei einer MDS-Lösung ist diese Linie außerdem streng monoton anwachsend (oder absteigend). Daraus läßt sich ein Verfahren zur Konstruktion von Zieldistanzen herleiten.

Im Fall einer ordinalen MDS muß die Rangordnung der Entfernungen genau der Rangordnung der Daten (also der Proximitäten) entsprechen. Alle Punkte, die in einem Shepard-Diagramm auf einer streng monoton steigenden Kurve liegen, erfüllen diese Bedingung. Da die Proximitätswerte bei der ordinalen MDS eben nur ordinale Information enthalten, sind die Distanzen invariant bezüglich ordnungserhaltender (streng monotone) Transformationen der Daten. Die Wahl dieser Kurve ist aber nicht ganz beliebig: Sie sollte nicht im Bereich zu kleiner oder zu großer Werte liegen, sondern in der Nähe der ``Zieldistanzen''. Außerdem sollten die Zieldistanzen so gewählt werden, daß sie nur minimal verändert werden müssen.

Die Kurve ist daher so durch das Shepard-Diagramm zu legen, daß die Punkte möglichst nahe an ihr liegen (in ihrer Distanzkomponente, also dem Abszissenwert). Dazu soll die Summe der quadrierten Abweichungen minimiert werden. Bezeichnet man die Zieldistanzen mit und die Abweichungen mit , dann muß für die MDS-Lösung der Ausdruck durch eine streng monotone Folge von minimiert werden. Dazu ist folgendes rechnerisches Vorgehen erforderlich:

1. Man geht von einer zufälligen Startkonfiguration aus.
2. Für die einzelnen Paare von Punkten der Ausgangskonfiguration werden die (euklidischen) Distanzen bestimmt.
3. Die Berechnung der Zieldistanzen ist etwas unhandlich: Die Distanzen werden in der Reihenfolge der entsprechenden Proximitäten betrachtet. Stimmt die Rangreihe zweier aufeinanderfolgender Distanzen nicht überein, werden diese beiden durch deren arithmetisches Mittel ersetzt; entspricht dann die Ordnungsrelation zu der nächsten Distanz (entsprechend der Rangreihe der Proximitäten) nicht, wird über alle drei Werte gemittelt usw. Man erhält auf diese Weise ``Blöcke'' gemittelter Werte , deren Rangreihe insgesamt mit derjenigen der Proximitäten übereinstimmt (es liegt aber keine strenge Monotonie vor).
4. Die Bestimmung der neuen Koordinaten der Punkte erfolgt ähnlich wie in Gleichung 2.1, allerdings werden hier anstelle der Werte der Rank Image-Matrix nun die Disparitäten (Zieldistanzen) eingesetzt:

    

5. Nach Korrektur aller Punkte erhält man eine neue Konfiguration, für die wieder ein Shepard-Diagramm erstellt wird und die monotone Regressionskurve berechnet wird. Insbesondere die Summe der quadrierten Abweichung zwischen den Distanzen und den Zieldistanzen ist gegenüber der vorherigen Konfiguration kleiner geworden.
6. Dieser Iterationszyklus wird solange wiederholt, bis man zu einer Konfiguration gelangt, deren Wertepaare im Shepard-Diagramm tatsächlich eine streng monoton ansteigende Kurve definieren. Die Fehlergröße nimmt dabei immer weiter ab (auch hier ergibt sich aber der größte Fortschritt in den ersten Iterationszyklen).

Behandlung von Missing Data und Ties

In diesem Abschnitt soll erläutert werden, wie mit fehlenden Werten (missing data) und identischen Datenwerten (ties) umgegangen werden kann; dabei wird wiederum von ordinalen Daten ausgegangen. Als Ausgangsbeispiel verwendet Borg (1981) eine Rangordnung von Unähnlichkeiten, die durch einen Card-Sort erhoben wurde (Einen Haufen an n Karten in ähnliche und unähnliche Teilmenge aufgliedern; diese Prozedur wird solange rekursiv wiederholt, bis eine Rangreihe gegeben ist). Das ähnlichste Paar erhält die Rangzahl 1, das unähnlichste die Rangzahl n.

Eine Variante des Card-Sorts könnte aber darin bestehen, daß die Versuchsperson Haufen von Karten, die sie für ununterscheidbar bezüglich des Kriteriums (Unähnlichkeit) hält, nicht weiter aufteilen muß. In diesem Fall ist zu erwarten, daß an beiden Enden der Ähnlichkeitsordnung relativ kleine Kartenhaufen entstehen, während im Bereich mittlerer Ähnlichkeiten die Stapel umfangreicher wären. Karten aus demselben Haufen wird dann auch derselbe Proximitätswert zugewiesen. Den gleichen Proximitätswerten muß aber nicht notwendigerweise auch die gleiche Distanz zugewiesen werden:

• primary approach to ties: Ties in den Daten werden nicht notwendigerweise auf gleiche Distanzen abgebildet, solange nur die Ordnungsbeziehungen zwischen den Blöcken gleicher Proximität auch derjenigen zwischen den entsprechenden Distanzblöcken entspricht. Ties können in den Distanzen aufgelöst oder gebrochen werden.
• secondary approach to ties: Bei Ties wird auch dieselbe Distanz zugeordnet. Dieser Ansatz wird bei einer metrischen MDS immer gewählt. Ansonsten wird dieses Modell gewählt, wenn relativ starke inhaltlich-theoretische Erwartungen bezüglich der Struktur einer MDS-Konfiguration existieren und dadurch getestet werden sollen, daß der Konfiguration diese Struktur aufgezwungen wird.

MDS-Analysen können auch für Korrelationsmatrizen (genaugenommen für Interkorrelationsmatrizen) durchgeführt werden, um Strukturhypothesen über die Variablen zu testen. Auch hierbei kann es zu Ties kommen, die aber verschwinden, wenn man die Korrelationen genauer berechnet (mehr Nachkommastellen). Allerdings weisen die Korrelationskoeffizienten keine große Zuverlässigkeit auf, da sie meist aus relativ kleinen Stichproben berechnet wurden. Daher ist es durchaus sinnvoll, ähnliche Korrelationen auch als Ties zu behandeln. Geringe Korrelationen (etwa kleinere als 0.2) können außerdem als nicht signifikant betrachtet werden und daher von der weiteren Betrachtung ausgeschlossen werden. Auf diese Weise können fehlende Werte (missing values) auftreten.

Aber auch bei fehlenden Werten können die Distanzen bestimmt werden. Eine Möglichkeit bestünde darin, die in der Datenmatrix fehlenden Zellen direkt mit den entsprechenden Distanzen zu füllen. Distanz und Zieldistanz sind für die Missing Data somit immer identisch, so daß die Punktbewegungen durch sie nicht beeinflußt werden. Beim Verfahren der monotonen Regression ändert sich nur der dritte Schritt: In der Matrix der Disparitäten setzt man für die fehlenden Werte die Distanzen ein; bei den restlichen Zellen geht man wie beschrieben vor.

Anstatt eine vollständige Matrix von Zieldistanzen zu erzeugen, kann man aber auch lediglich Rank-Image-Werte oder Disparitäten für die Zellen berechnen, die keine Missing Data enthalten, so daß sich folgende Korrekturformel ergibt:

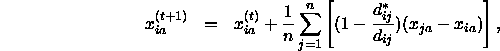
wobei , wenn undefiniert ist.

Im primären Ansatz sortiert man für die Bildung des Rank Images die Distanzen entsprechend der Rangreihe der Proximitäten und permutiert dann innerhalb von Tie-Blöcken derart, daß die jeweiligen Rangordnungen denen der Daten (Proximitäten) entsprechen. Im sekundären Ansatz ersetzt man alle Rank Image-Werte innerhalb eines Tie-Blocks durch das arithmetische Mittel der Distanzen, die dort nach Durchführung des Sortiervorgangs stehen.

Die Berechnung der Disparitäten für die monotone Regression ist etwas komplizierter: Beim primären Ansatz werden die Distanzen zuerst so geordnet, daß sie innerhalb von Tie-Blöcken monoton abfallen. Anschließend werden die Disparitäten wie in Abschnitt 2.5 beschrieben berechnet. Die so erhaltenen Werte für die Zieldistanzen werden dann der ursprünglichen Ordnung der Paare zugeordnet. Für den sekundären Ansatz werden zunächst die Distanzwerte innerhalb der Tie-Blöcke gemittelt und dann wird - wie üblich - durch Block-Erweiterung und Durchschnittsbildung fortgefahren, bis eine monotone Folge von Werten erzeugt ist.

Last modified 10-29-98