Multidimensionale Skalierung ist die Bezeichnung für eine Gruppe von Methoden, die Reizähnlichkeiten räumlich repräsentieren wollen. Diese Methoden erlauben es, aus ordinalen Annahmen über die Daten zu metrischen euklidischen Distanzen der zu beurteilenden Objekte zu gelangen. Im Gegensatz zur Faktorenanalyse können auch Daten eingesetzt werden, die an wenigen Versuchspersonen und unter wenigen Grundannahmen erhoben werden. Das hauptsächliche Ziel ist eine sparsame (parsimonious) räumliche Repräsentation der Objekte.
In der Tradition von Fechner wird versucht, eindimensionale Skalierungsverfahren zu entwickeln, die dem physikalischen Kontinuum zugeordnete subjektive Empfindungen meßbar machen sollen (psychophysische Funktion). Am Anfang stand der Ansatz von Thurstone, das law of comparative judgment, bei dem ein Attribut des Reizes variiert wird und die Beurteiler angewiesen werden, ihre Urteilsbildung nach dieser Dimension zu organisieren.
Bei der multidimensionalen Skalierung (MDS) wird der subjektiven Ähnlichkeit zwischen Objekten eine metrische Distanz zwischen Punkten im mehrdimensionalen Raum zugeordnet. Ahrens (1974) spricht von einem subjektiven oder psychologischen Reizraum, dessen metrische und dimensionale Repräsentation das Ziel der multidimensionalen Skalierung darstellt. MDS-Modelle werden oft als geometrische Dekompensationsmodelle bezeichnet, deren Grundlage eine gewisse Zerlegbarkeit der Ähnlichkeitsdaten darstellt.
Die der MDS zugrundeliegenden Ähnlichkeitsdaten können z.B.
Die Objekte werden als Punkte eines metrischen Raumes betrachtet, der nach expliziten Vorschriften des Skalierungsmodells so aufgespannt wird, daß bei minimaler Dimensionalität die beobachteten Reizähnlichkeiten möglichst genau durch die Punktdistanzen approximiert werden.
Bei Verwendung euklidischer Distanzen besteht eine große Ähnlichkeit zwischen MDS und Faktorenanalyse. MDS kommt aber eher aus der Tradition der Psychophysik und soll diejenigen Attribute messen, die der subjektiven Beurteilung komplexer Reizobjekte vermutlich zugrunde liegen. Es werden also quantitative Informationen über latente Meßdimensionen der Reizobjekte hergeleitet. Es handelt sich um ein Verfahren zur Gewinnung von Meßdaten, während die Faktorenanalyse eher zu deren Analyse eingesetzt wird.
Im weiteren Sinne kann man die MDS als Methode zur quantitativen Strukturierung von multivariaten Verhaltensinformationen ansehen; es handelt sich damit eher um ein meßtheoretisches Verfahren als um ein statistisches. Man kann daher MDS auch als Spezialfall von Methoden der Strukturanalyse und dimensionalen Reduktion multivariater Beobachtungen oder sogar als psychologische Theorie der subjektiven Reizähnlichkeit betrachten. Man kann MDS auch als strukturelle Basis von Verhaltenstheorien ansehen, beispielsweise als Theorie der Urteilsbildung oder als Wahrnehmungstheorie. Der theoretische Erklärungswert eines MDS-Modells muß auf drei Ebenen gerechtfertigt werden (was aber in der Praxis nur in den seltensten Fällen getan wird):
Bei der Analyse von MDS-Modellen muß auch die interindividuelle Heterogenität der Beurteiler beachtet werden, also die ``Beurteiler 
Reizobjekt''-Interaktion. Aus der Perspektive der allgemeinen Psychologie und der Psychophysik werden individuelle Unterschiede als Störgröße betrachtet, die ``herausgemittelt'' werden soll, um zu möglichst allgemeinen Aussagen zu gelangen; dies gilt auch für die meisten MDS-Analysen. Man kann aber auch eine differentialpsychologische Basis der MDS berücksichtigen, indem intraindividuell gegliederte subjektive Reizstrukturen in Abhängigkeit von systematischen interindividuellen Unterschieden der Beurteiler skaliert werden.
Eine Datentheorie nach Coombs soll die Zusammenhänge zwischen Meßwerten und Beobachtungsdaten klären und Konzepte bereitstellen, die der Strukturierung von Datenerhebungsmethoden und Meßverfahren in verschiedenen Verhaltensbereichen dienen. Geometrische Modelle beschreiben das Verhalten als Relationen zwischen Punkten im metrischen Raum. Eine empirisch bedeutsame Messung (Abbildung eines empirischen Relativs in ein numerisches) muß zwei grundlegende Anteile enthalten:
Das empirische Relativ von Personenurteilen, das in Form von Dominanzrelationen (a wird vor b bevorzugt bzw. Präferenzwahrscheinlichkeiten in einer Dominanzmatrix) oder Ähnlichkeitsrelationen (direkte Einschätzung der Ähnlichkeit zweier Reize oder indirekte über Tripelvergleiche, bei denen angegeben werden muß, welcher von zwei Reizen einem dritten ähnlicher ist.) vorliegt, soll also in ein numerisches Relativ abgebildet werden. Es sind auch probabilistische Skalierungsmodelle denkbar, etwa nach dem Luce'schen Wahlaxiom.
Bei der Unfolding-Skalierung werden auf der Grundlage von expliziten Präferenzurteilen von Versuchspersonen implizite Ähnlichkeitsbeziehungen zwischen ihrem Idealpunkt auf einem individuellen Kontinuum und den Reizpunkten hergestellt. Solche im Idealpunkt I einer Person gefaltete Skalen nennt man I-Skala; Ziel der Skalierung ist es, aus den verschiedenen I-Skalen zuerst eine gemeinsame qualitative J-Skala (joint scale) zu entfalten, auf der sich Personen und Objekte gemeinsam abbilden lassen. Unter geeigneten Voraussetzungen (z.B. Eindimensionalität) läßt sich dann aus den Ranginformationen über die Reizähnlichkeiten eine quantitative J-Skala herleiten, die metrische Aussagen über die Ähnlichkeiten bzw. Distanzen der Reize zuläßt. Das Unfolding-Modell wurde auch für mehrdimensionale Ansätze erweitert.
Besonders wichtig im Rahmen der MDS sind Proximitätsdaten. Dabei kann es sich um
-Matrizen vor, deren Zeilen/Spalten den n vorgegebenen Reizobjekten entsprechen. Zwischen den Ähnlichkeitsmaßen (Proximitäten) 
und den Distanzen 
in der MDS-Repräsentation soll dabei zumindest eine monotone Beziehung bestehen.
Ahrens (1974) untersucht außerdem das Repräsentationsproblem (Postulieren einer homomorphen/isomorphen Abbildung von den empirischen Strukturen in die Zahlen), das Eindeutigkeitsproblem
(Skalenniveau aufgrund der Zuordungsvorschrift von den empirischen in die numerischen Strukturen) und das Bedeutsamkeitsproblem (spezifische Bedeutung der numerischen Aussagen für das empirische System).
Das Konzept der Ähnlichkeit (Proximität) von Reizen bildet die Grundlage der MDS-Skalierung. Dabei handelt es sich um eine zwei- oder dreistellige Relation. Bei der MDS wird die Versuchsperson nicht explizit instruiert, die Ähnlichkeit hinsichtlich bestimmter Reizmerkmale zu beurteilen, sondern es wird nach der globalen Ähnlichkeit gefragt. Durch beobachtbare Reizähnlichkeiten sollen latente Reizdimensionen geschätzt werden. Dem liegt das theoretische Konstrukt der Existenz einer subjektiven Reizstruktur mit latenten Ähnlichkeitsrelationen zugrunde.
Die Reizähnlichkeiten werden durch die MDS in einem mehrdimensionalen metrischen Raum durch metrische Distanzen repräsentiert. In diesem Sinne spricht man von der Konstruktion eines mehrdimensionalen subjektiven Ähnlichkeitsraumes oder kurz von einem ``psychologischen Raum''. Die Distanzfunktion dieses psychologischen Raumes wird als Modell der zugrundeliegenden subjektiven Prozesse interpretiert, nämlich als Kombiationsregeln für die Bildung von Ähnlichkeitsurteilen in den Dimensionen des metrischen Bildraumes.
Die Aufgabe der Analyse subjektiver Reizähnlichkeiten wird im Prinzip so gelöst, daß man zunächst die Existenz eines empirisch zugänglichen Raumes subjektiver Ähnlichkeitsrelationen zwischen Reizen postuliert. Dann versucht man, die empirischen Reizähnlichkeiten isomorph (bzw. homomorph) in ein numerisches Relativ abzubilden, das strukturell durch einen metrischen Modellraum beschrieben wird, in welchem die Reizähnlichkeiten als metrische Punktdistanzen repräsentiert werden. Die Abbildungsvorschriften sind formal in dem jeweils verwendeten MDS-Modell zusammengefaßt.
Durch diese numerischen Zuordnungen wird im Rahmen der verwendeten Distanzfunktion beschrieben, nach welchen spezifischen Anteilen sich die globalen Reizähnlichkeiten strukturieren: Die globale Distanz d(x, y) zweier Reize i und j wird als Funktion ihrer spezifischen Distanzen 
in den einzelnen Dimensionen i des Abbildungsraumes dargestellt. Damit besteht die wichtigste Aufgabe der Ähnlichkeitsskalierung in der Konstruktion einer geeigneten Distanzfunktion, die angibt, wie und in welcher Metrik die globalen Distanzen aus latenten Reizattributen kombiniert werden können. Dabei müssen die folgenden fundamentalen Axiome einer Metrik erfüllt sein:
.
.
Die Art der Metrik kommt in der Definition des Abstandes d(x,y) zweier Punkte x und y zum Ausdruck, wobei die globalen Distanzen d(x,y) als Funktion der spezifischen Distanzen in n Dimensionen ausgedrückt werden. Für MDS-Modelle werden folgende Metriken eingesetzt:
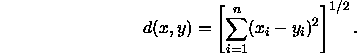
Euklidische Distanzen sind invariant gegenüber einer Translation des Nullpunktes und gegenüber orthogonaler Achsenrotation; dadurch können, wie auch bei der Faktorenanalyse, die Achsen so gewählt werden, daß sie psychologisch sinnvoll interpretierbar sind. Bei einer Streckung werden die Distanzen dagegen um den Streckungsfaktor verlängert.
City-Block-Distanzen sind - wie alle nichteuklidischen Metriken - nicht invariant gegenüber orthogonaler Achsenrotation. Dadurch wird deren praktische Brauchbarkeit stark eingeschränkt.
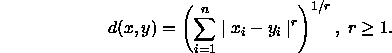
Hierbei nennt man r auch die Minkowski-Konstante. Bei r=1 erhält man eine City-Block-Metrik und bei r=2 eine euklidische Metrik. Alle r-Metriken sind zwar invariant gegenüber Verschiebungen des Nullpunkts, aber nur für den Fall von r=2 liegt auch eine Invarianz gegenüber orthogonalen Achsenrotationen vor.
Ahrens (1974) beschreibt verschiedene Verfahren zur MDS. Bei der multidimensionalen Skalierung euklidischer Distanzen nach Torgerson muß berücksichtigt werden, daß es sich bei den Proximitäten um subjektive Schätzungen handelt, die mit einem Fehler behaftet sind. Daher würden man zu unterschiedlichen Konfigurationen gelangen, je nachdem, welchen Punkt man als Ursprung verwenden würde. Um diese Fehler auszugleichen, legt man den Ursprung der Vektoren in den Schwerpunkt der Reizkonfiguration (und hofft, daß so unsystematische Fehler herausgemittelt werden). Zur empirischen Gewinnung der Ähnlichkeitsurteile wird häufig die Methode der vollständigen Triaden verwendet.
In einer ersten Stufe (Distanzmodell) wird eine eindimensionale Skalierung der Ähnlichkeit durchgeführt, die zu vorläufigen Distanzen aufgrund von komparativen Ähnlichkeitsurteilen führt: Aus den beobachtbaren Ähnlichkeitsurteilen werden Distanzen bestimmt. In einer zweiten Stufe (Raummodell) folgt eine metrische und dimensionale Einbettung der Distanzen, so daß die Distanzen auf eine Menge von Reizkoordinaten (als möglichst geringe Punktabstände) in möglichst wenigen Dimensionen reduziert werden. Die Achsen dieses psychologischen Raumes sind die gesuchten Skalen und sie werden auch als subjektive Unterscheidungsvariable interpretiert.
Bei der nonmetrischen MDS wird nicht zwischen dem Raummodell und dem Distanzmodell getrennt, beide werden gleichzeitig bestimmt. Außerdem wird keine bestimmte Funktionsform für die Umwandlung von empirischen Ähnlichkeitswerten in metrische Distanzmaße postuliert, sondern es wird nur ein monotoner Zusammenhang zwischen empirischen Ähnlichkeiten und metrischen Distanzen angenommen. Es soll lediglich die Rangordnung beobachteter Unähnlichkeiten in den Reizpaaren durch die Ordnung ihrer metrischen Konfigurations-Distanzen approximiert werden.
Bei dem Ansatz von Shepard wird die metrische Konfiguration aus ordinaler Information konstruiert: Es wird eine minimale Anzahl kartesischer Koordinaten ermittelt, wobei die Ausgangsinformation nicht durch metrische Punktdistanzen, sondern nur durch eine unbekannte Funktion dieser Distanzen dargestellt wird. Durch eine monotone Transformation von Proximitätsmaßen erhält man explizite Distanzen in einem euklidischen Raum minimaler Dimensionalität. In einer simultanen Prozedur sollen also folgende zwei Ziele erreicht werden:
in euklidische Distanzen und
mit 
(wobei r die Dimensionalität des metrischen Raumes bezeichnet.
Die Güte der Anpassung einer MDS-Lösung muß in bezug auf die Zielsetzung der MDS bestimmt werden. Folgende beiden Zielsetzung sind möglich:
Wie bei jeder multivariaten Dimensionsanalyse stellt sich auch bei der MDS das Problem der inhaltlich-psychologischen Interpretation der metrischen Repräsentation der skalierten Ähnlichkeitsdaten. Dies ist insbesondere dann schwierig, wenn die MDS zur Erzeugung neuer Strukturhypothesen eingesetzt wird. Dabei werden drei Methodengruppen unterschieden: