Das -System

Nun solle eine konkrete Realisierung der zuvor abstrakt eingeführten numerischen Farbrepräsentation vorgestellt werden. Das -System (tristimulus color-space) ist ein Koordinatensystem, das aus den drei Primärfarben Rot , Grün und Blau besteht; diese Farben sind so definiert, daß durch einen monochromatischen Reiz der Wellenlänge 700 nm realisiert wird, durch einen monochromatischen Reiz der Wellenlänge 546.1 nm und durch einen monochromatischen Reiz der Wellenlänge 435.8 nm. Jeder der drei Farben entspricht dabei eine Achse (bzw. ein Basisvektor) des Farbraumes. Diese Achsen besitzen einen gemeinsamen Ursprung und dürfen nicht alle in einer Ebene liegen (d.h. sie müssen linear unabhängig sein); sie müssen nicht senkrecht aufeinander stehen.

Jeder Farbreiz S läßt sich in diesem System durch einen Vektor repräsentieren. Nun Bezeichne R die Intensität des Primärreizes in einer Mischung, G die Intensität von und B die Intensität von ; man nennt R, g und B auch die Farbwerte dieser Mischung. Gleiche Beträge von R, G und B bewirken ein neutrale Farbe N. Die Einheitsebene (unit plane oder auch chromaticity diagram genannt) wird durch die Punkte , und aufgespannt. Sie läßt sich auch folgendermaßen definieren:

Innerhalb dieses Farbraums kann die Mischung zweier Farben als Vektoraddition betrachtet werden. Der Farbvektor S einer beliebigen Farbe (bzw. dessen Verlängerung) schneidet die Einheitsebene; dieser Schnittpunkt S heißt Farbort oder chromaticity point der Farbe S. Der Punkt S besitzt die drei Farbwerte R, G und B bzw. die Farbwertanteile r, g und b. Geometrisch lassen sie sich folgendermaßen veranschaulichen: In einem Dreieck, dessen Eckpunkte die Primärreize , und bilden (siehe Abbildung 6), berechnen sich die Koordinaten von S folgendermaßen:

 
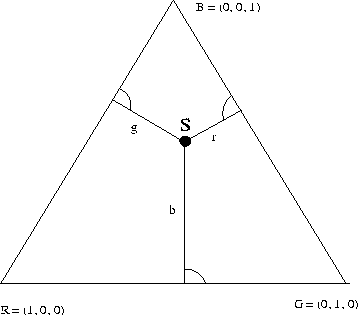
Abbildung 6:   Koordinaten der Farbe S im -System: Diese Skizze zeigt die durch die Primärfarben , und aufgespannte Ebene und die Farbwertanteile r, g und b einer Farbe S.

• r ist der Abstand von S zu der Verbindung von und :
  
  
• g ist der Abstand von S zu der Verbindung von und :
  
  
• b ist der Abstand von S zu der Verbindung von und :
  
  

Man kann aber auch andere Primärreize als , und verwenden, beispielsweise die ``imaginären'' Reize , und . Dann ist folgende Umrechnung erforderlich:

wobei die Anteile der jeweiligen Farbe (gemischt aus ) bezeichnet, um einen Abgleich zu der Farbe (R = 1, G = 0, B = 0) herzustellen; bezeichnen die Anteile zum Abgleichen von (R = 0, G = 1, B = 0) und bezeichnen die Anteile für eine Farbgleichheit zu (R = 0, G = 0, B = 1).

Diese Transformationsmatrix beschreibt also die Beziehung zwischen zwei Mengen an Primärfarben , und und , und eindeutig. Für die Farbwerte ließe sich ebenfalls eine (etwas kompliziertere) Transformation angeben; bei dieser handelt es sich um eine projektive Transformation in der Ebene (diese Ebene ist übrigens die Einheitsebene).

Somit gilt: Einer linearen Transformation (bzw. einer affinen) des -Systems entspricht eine projektive Transformation der Farbwerte.

zurück zur Hauptseite (Farbwahrnehmung)
zurück zu meiner homepage

Anmerkungen und Mitteilungen an

Last modified 11-5-98