Diese Seite kann auch als Postscript-Datei geladen werden.

Reelle Zufalsvariablen

DEFINITION: Sei X eine Zufallsvariable. Die Funktion

heißt Verteilungsfunktion von X. Meist schreibt man kurz anstelle von . Für Verteilungsfunktionen gilt:

1. Sie sind monoton steigend. d.h. wenn , dann ist auch .
2. Für kleine Werte von x nähert sich F(x) an Null an: .
3. Für große Werte von x nähert sich F(x) an Eins an: .

DEFINITION: Zufallsvariablen, die nur Werte aus annehmen, werden reelle Zufallsvariablen genannt. Eine reelle Zufallsvariable besitzt eine Wahrscheinlichkeitsdichte f, falls für die Verteilungsfunktion F eine entsprechende Funktion f existiert, für die gilt:

 

Die Funktion f muß insbesondere stetig sein. Aus der Gleichung 1 folgt

Erwartungswert

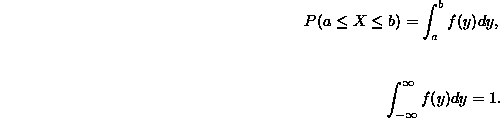
DEFINITION: Der Erwartungswert einer Zufallsvariable ist im diskreten Fall folgendermaßen definiert:

Im stetigen Fall lautet die Definition

wobei . Es handelt sich also in beiden Fällen um eine (mit den Auftretenswahrscheinlichkeiten) gewichtete Summe von Werten. Zu den Rechenregeln für Erwartungswerte findet sich im Anhang B des Buches von HAYS (1988) eine brauchbare Zusammenfassung.

Besonders wichtig ist, daß der Erwartungswertoperator linear ist: Seien X und Y Zufallsvariablen über dem selben Wahrscheinlichkeitsraum mit den Erwartungswerten und und sei . Dann gilt Homogenität und Additivität:

Die Linarität ist eine sehr wünschenswerte Eigenschaft, da sie eine Dekomponierbarkeit der Wirkung mehrerer Faktoren erlaubt (jeder einzelne Faktor läßt sich sozusagen einzeln rausrechnen).

Rechnen mit Erwartungswerten

Da Erwartungswerte (vor allem auch in der Testtheorie) eine sehr bedeutende Stellung einnehmen, möchte ich an dieser Stelle einige wichtige Rechenregeln nennen. Zuerst nochmals die Definition des Erwartungswertes einer Zufallsvariable X:

wobei die Summe über alle möglichen Ausprägungen der Zufallsvariable X ist. Nun folgen die Rechenregeln (die übrigens auch für den stegigen Fall gelten):

1. Handelt es sich bei a um eine Konstante, dann

   

2. Handelt es sich bei a um eine konstante reelle Zahl und sei X eine Zufallsvariable mit dem Erwartungswert , dann

   

3. Handelt es sich bei a um eine konstante reelle Zahl und sei X eine Zufallsvariable, dann

   

4. Sei X eine Zufallsvariable mit dem Erwartungswert und sei Y eine Zufallsvariable mit dem Erwartungswert , dann

   

5. Es sei eine endliche Anzahl von Zufallsvariablen gegeben; der Erwartungswert der Summe dieser Variablen ist gleich der Summe der Erwartungswerte der einzelnen Variablen. Es gilt also beispielsweise

   

6. Sei X eine Zufallsvariable mit dem Erwartungswert und sei Y eine Zufallsvariable mit dem Erwartungswert ; wenn X und Y stochastisch unabhängig sind, gilt

   

   Nebenbemerkung: Ist , dann sind die Variablen X und Y nicht unabhängig.

7. Es sei eine endliche Anzahl von Zufallsvariablen gegeben, die paarweise unabhängig sind; der Erwartungswert des Produkte dieser Variablen ist gleich dem Produkt der Erwartungswerte der einzelnen Variablen. Es gilt also beispielsweise

   

Varianz

Die Varianz bezeichnet die mittlere quadrierte Abweichung vom Erwartungswert; somit gilt im diskreten Fall:

und im stetigen Fall gilt

wobei f(x) die Wahrscheinlichkeitsdichte der Zufallsvariable X bezeichnet. Die Standardabweichung von X ist die positive Wurzel aus der Varianz.

Zur praktischen Berechnung der Varianz wird häufig die folgende einfachere Formel verwendet; sie läßt sich folgendermaßen herleiten:

Rechnen mit Varianzen

1. Handelt es sich bei a um eine konstante reelle Zahl und sei X eine Zufallsvariable mit dem Erwartungswert und der Varianz , dann, dann besitzt die Zufallsvariable (X + a) folgende Varianz:

   

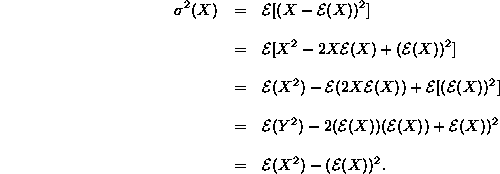
   Deshalb muß auch gelten .

2. Handelt es sich bei a um eine konstante reelle Zahl und sei X eine Zufallsvariable mit der Varianz , dann, dann besitzt die Zufallsvariable (aX) folgende Varianz:

   

Diese Formeln wurden folgendem Buch entnommen:

Hays, W. L. (1973). Statistics for the social sciences, 2nd ed. London et al.:Holt, Rinehart and Wilston.

Kovarianz und Korrelation

DEFINITION: Seien X und Y zwei Zufallsvariablen. Der Erwartungswert

 

heißt Kovarianz von X und Y. Anstelle von schreibt man auch oder Cov(X, Y). Es läßt sich zeigen, daß gilt

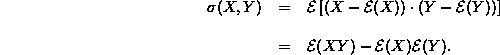
Die Kovarianz von zwei Zufallsvariablen hängt stark von der Varianz der einzelnen Variablen ab, wie man in Gleichung 2 sieht (es werden auch Abweichungen zum Erwartungswert betrachtet, nur keine quadrierten). Sucht man ein Maß des Zusammenhangs (bzw. gemeinsamen Variierens) zweier Zufallsvariablen, das nicht von deren Streuung abhängt, berechnet man die Korrelation:

DEFINITION: Sind X und Y Zufallsvariablen, dann heißt

der Korrelationskoeffizient von X und Y; Statt schreibt man auch .

Rechnen mit Kovarianzen und Korrelationen

Für zwei Zufallsvariablen X und Y und reelle Konstanten a, b gelten folgende Rechenregeln:

1. .
2. Sind X und Y stochastisch unabhängig, dann ist die Varianz der Summe gleich der Summe der Varianzen:

   

   ist dagegen die Kovarianz der beiden Zufallsvariablen von Null verschieden, dann lautet der Zusammenhang

   

3. .

Eine besonders wichtige Anwendung der Korrelation in der Testtheorie besteht in der Überprüfung der Güte von Tests. Die Validität eines Tests bezeichnet dessen Korrelation mit einem Außenkriterium; die Reliabilität bezeichnet den Meßfehler des Tests, also das Verhältnis der Varianz des wahren Wertes zur Varianz der beobachteten Werte; sie wird als Quadrat der Korrelation zwischen wahrem Wert und Beobachtungswert berechnet.

Ein Beispiel für die Korrelation

In diesem Beispiel ist eine mittlere Korrelation von 0.53 veranschaulicht: Der Zusammenhang zwischen Anzahl abgearbeiteter Stunden und der dafür bezahlten Vergütung sei nicht deterministisch (nämlich 10 DM pro Stunde), sondern schwanke zufällig, so daß insgesamt eine Korrelation von 0.53 besteht, wie sie für sehr gute psychologische Test als maximale Validität erreicht werden kann.

Die Zufallsvariable Arbeitsstunden sei normalverteilt mit einem Mittelwert von 50 und einer Standardabweichung von 20. Es werden 100 derartige Arbeitszeiten zufällig bestimmt. Zu jeder dieser Zeiten wird der Stundenlohn berechnet, der sich ergibt wenn genau 10 DM pro Stunde bezahlt werden. Dieser ``deterministische'' Lohn wird dann mit einer zufälligen normalverteilten Schwankung (durch Ausprobieren ergab sich, daß eine Standardabweichung von 300 zur gewünschten Korrelation führt) versehen, so daß sich eine Korrelation von 0.53 zwischen den beiden zufallsvariablen ergibt. Die so bestimmten datenpunkte sind in der folgenden Abbildung zu sehen.

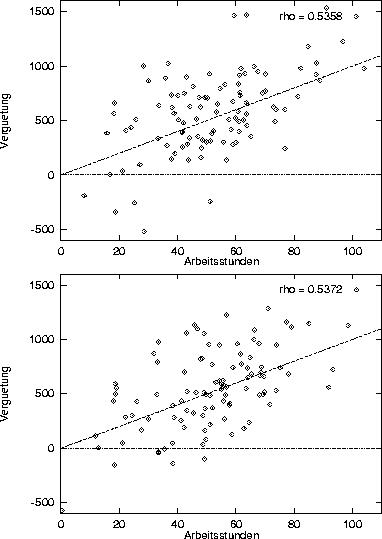
Dieses Beispiel soll demonstrieern, daß eine Korrelation von 0.53, wie sie maximal bei psychologischen Tests erreicht werden kann, sehr starke Schwankungen zuläßt. Die Überprüfung der Homogenität der Probanden mit gleichem Rohwert durch die Korrelation der Testergebnisse mit einem Außenkriterium ist deshalb sehr ungenau.

Kombinatorik

Es sei ein Test mit k Aufgaben gegeben, zu denen es jeweils m Antwortalternativen gibt. Dann gibt es insgesamt verschiedene Lösungsmuster (wird nur zwischen richtigen und falschen Lösungen unterschieden, reduziert sich diese Anzahl auf .

Wird nur die Summe der richtig gelösten Aufgaben betrachtet, dann spielt es keine Rolle, welche Aufgaben im Einzelnen gelöst gelöst wurden. Wird nur zwichen richtigen und falschen Lösungen unterschieden, dann berechnet sich die Anzahl N der verschiednen Möglichkeiten, bei denen genau k der insgesamt n Aufgaben richtig gelöst sind, folgendermaßen:

Erschöpfende Statistik

Eine andere Möglichkeit zur Überprüfung, ob sich Personen mit gleicher Anzahl gelöster Aufgaben in ihrer tatsächlichen Merkmalsausprägung untercheiden, führt über die Betrachtung von erschöpfenden (suffizienten) Statistiken.

Definition Statistik: Eine Statistik ist eine Abbildung

eine Statistik ist also eine Abbildung eines n-elementigen Zufallsvektors (Daten) auf ein r-dimensionales Tupel von (geschätzten) Parametern.

Nun werden die Ergebnisse des Test des Probanden h, der die wahre Fähigkeit besitzt, untersucht; Das Ergebnis des Tests liege als Antwortvektor vor; die Statistik bezeichne die Anzahl der in diesem Antwortvektor vorkommenden richtig gelösten Aufgaben.

Nach der Definition der Bedingten Wahrscheinlichkeit gilt dann:

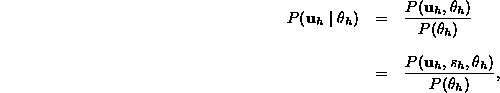
weil die Statistik eine Funktion der Daten ist und somit die Wahrscheinlichkeit nicht verändert. Nun wird wieder die Formel der bedingten Wahrscheinlichkeit eingesetzt:

 

Die Gleichung 3 gilt für jede Statistik; demgegenüber wird für erschöpfende Statistiken folgende Einschränkung gefordert:

Für erschöpfende Statistiken gilt somit

dies bedeutet, daß die Wahrscheinlichkeit für einen bestimmten Antwortvektor bei gegebener Anzahl gelöster Aufgaben nicht weiter von der Personenfähigkeit abhängt, als durch die Statistsik bereits erfaßt ist. Dies wiederum kann so interpretiert werden, daß bei gleicher Statistik keine Unterschiede zwischen den Personenfähigkeiten bestehen. Genau dies will man mit einer erschöpfenden Statistik erreichen.

Trifft also die Erschöpfungseigenschaft zu, dann darf die Anzahl richtig gelöster Aufgaben als sinnvoll interpretierbares Testergebnis verwendet werden.

Entscheidungstheoretische Überlegungen

Angenommen, man will aufgrund eines Testergebnisses die Eignung eines Probanden für eine bestimmte Tätigkeit vorhersagen. Probanden ab einem Testwert von werden für die Tätigkeit akzeptiert; tatsächlich geeignet sind diejenigen, deren Bewährungskriterium Y über der Schwelle liegt. Bei einer binären Selektionsentscheidung sind dann immer vier Fälle zu betrachten:

wahr, akzeptiert:

richtige Entscheidung, true negatives. ; hit

wahr, abgelehnt:

falsche Entscheidung, false positives. Fehler 2. Art, -Fehler; ; miss

falsch, akzeptiert:

falsche Entscheidung, false negatives. Fehler 1. Art, -Fehler; ; false alarm

falsch, abgelehnt:

richtige Entscheidung, true positives; (Power eines Tests); correct rejection

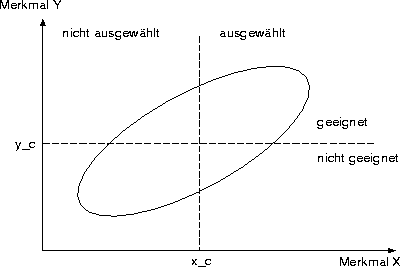
zurück zur Übungsseite

zurück zu meiner homepage