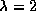. Wir haben also einen Poisson-Prozeß mit
der Intensität 2.
Hausaufgabe: Man stelle sich den Eingang eines Kaufhauses vor, an dem ein Drehkreuz angebracht ist, das jedesmal, wenn eine Person das Haus betritt, einen Impuls aussendet. Langfristige Erhebungen haben gezeigt, daß durchschnittlich zwei Kunden pro Minute eintreten. (Dabei kann es natürlich auch passieren, daß in einer Minute niemand oder auch beispielsweise 15 Personen das Drehkreuz passieren.) Wie hoch ist die Wahrscheinlichkeit, daß in einer Minute maximal 5 Kunden eintreffen?
Lösung: Jede mögliche Anzahl an Kunden, die innerhalb einer
bestimten Minute ankommen, besitzt eine gewisse Wahrscheinlichkeit.Der
Erwartungswert der Anzahl an Kunden, die pro Minute eintreffen,
beträgt 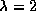. Wir haben also einen Poisson-Prozeß mit
der Intensität 2.
Die Wahrscheinlichkeit, daß in einer Minute maximal 5 Kunden
eintreffen, ist die Summe der Wahrscheinlichkeiten dafür, daß
genau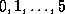 
Kunden innerhalb einer Minute eintreffen; also
müssen zuerst diese Einzelwahrscheinlichkeiten berechnet werden:
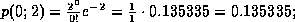
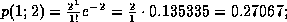
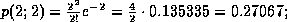
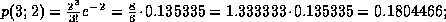
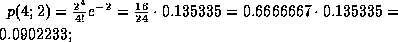
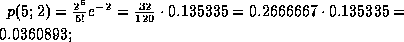
Um die Wahrscheinlichkeit dafür zu erhalten, daß maximal 5 Leute ankommen, müssen nun diese Einzelwahrscheinlichkeiten aufsummiert werden:
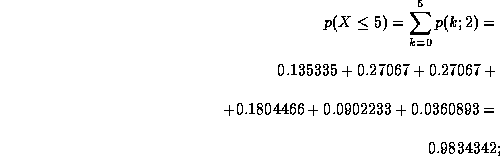
Die gesuchte Wahrscheinlichkeit beträgt also .9834342; es werden also mit sehr hoher Wahrscheinlichkeit (in über 98 von 100 Fällen) maximal 5 Leute pro Minute ankommen.
zurück zur Übungsseite (Unfällerproblem)
zurück zu meiner homepage
Anmerkungen und Mitteilungen an
rainer@zwisler.de