Rainer Zwisler
zurück zu meiner Skriptenseite
zurück zu meiner homepage
Die folgenden Definitionen wurden entnommen aus:
Wyszecki, Günter und Stiles, W.S. (1982). Color Science: Concepts and Methods, Quantitative Data and Formulae, 2nd Edition. New York: John Wiley & Sons.
ergibt sich aus dem Betrag einer bestimmten Quantität (die Wellenlängen in einem infinitesimalen Intervall besitzt, das die gegebene Wellenlänge enthält) dividiert mit der Breite des Intervalls. Die übliche Notation lautet:
welches für 
zur spektralen Verteilungsfunktion des Strahlungsflusses wird.
welches 
für die relative spektrale Verteilungsfunktion des Strahlungsflusses wird.
Reflexion bezeichnet den physikalischen Prozeß, durch den monochromatische Strahlungsenergie, die auf ein Material auftrifft (zumindest teilweise) durch das Material zurückgeworfen wird, ohne daß dadurch die Wellenlänge verändert wird.
Die grundlegende, die Reflexion kennzeichnende Quantität ist die
Reflektanz 
, die definiert wird als das Verhältnis des
reflektierten Strahlungsflusses 
zu dem eintreffenden
Strahlungsfluss 
:
Folgende Begriffe sind in diesem Zusammenhang von Interesse:
Farbmessung (colorimetry) ist das Teilgebiet der Farbforschung, das sich mit der numerischen Spezifizierung der Farbe eines physikalisch definierten visuellen Stimulus beschäftigt, wobei folgende Punkte gelten:
Ein sehr wichtiges Konzept in diesem Zusammenhang ist das der additiven Farbmischung. Darunter versteht man, daß ein Farbreiz mit Strahlungsenergie aus einem beliebigen (engen oder breiten) Intervall beliebiger Wellenlänge gleich der Summe der Strahlungsstärken der Konstitutenten der Mischung (die optisch unzusammenhängend sein sollen) in diesem Intervall ist. Dabei sollen folgende vier Gesetze gelten:
und
überein, wobei 
jeder positive Faktor
sein kann, mit dem die Strahlungsenergie des Farbreizes erhöht
oder verringert werden kann, während die relative spektrale
Verteilung gleich bleibt.
Über einen weiten Bereich an Beobachtungsbedingungen können viele Farbreize vollständig durch additive Mischung der drei festgelegten Primärfarben (deren Strahlungsintensitäten entsprechend festgelegt wurden) erstellt werden. Andere Farbreize müssen mit einer der beiden Primärfarben gemischt werden, bevor sich eine vollständige Übereinstimmung mit einer Mischung der verbleibenden beiden Primärfarben erstellen läßt. Für eine bestimmte Menge an Primärfarben existieren sogar Farbreize, die mit zwei der drei Primärstimuli gemischt werden müssen, um eine Übereinstimung mit der dritten Primärfarbe erzielen zu können.
Die Auswahl der drei Primärfarben kann aus einem breiten Bereich erfolgen, ist jedoch nicht vollkommen beliebig. Keine der drei Primärfarben darf sich durch Mischung der beiden anderen Primärfarben erstellen lassen.
Farbstimuli lassen sich eindeutig charakterisieren durch ihre
jeweilige absolute spektrale Shrahlstärke-Verteilungen
. Die spektrale Verteilung eines bestimmten
Farbreizes Q wird bezeichnet durch 
. Die Primärfarben werden durch Mulitiplikation mit
einer Konstanten als primäre Stimuli von Einheitsbeträgen
(primary stimuli of unit amounts) betrachtet und
folgendermaßen bezeichnet:
bezeichnet R;
bezeichnet G;
bezeichnet B.
Die Werte für , 
und 
sind konstante
positive Faktoren, die nach Bequemlichkeitsaspekten gewählt werden können.
Als Einheitswerte werden diejenigen Werte der Primärreize verwendet,
die bei additiver Mischung einen vollständigen Match mit einem
vorher spezifizierten achromatischen Reiz ergeben.
Mit der hier dargestellten Notation läßt sich ein Match zwischen dem Reiz Q und der Mischung geeigneter Beträge der Primärreize R, G und B durch folgende Gleichung beschreiben:
Dabei werden die skalaren Multiplikatoren 
, 
und
, die entsprechend den Einheiten der gegebenen Primärreize
gemessen werden, als Tristimulus-Werte (tristimulus values)
von Q bezeichnet.
) in Richtung der Violettlinie entfernt ist.
Folgende Formel gilt für die Berechnug der Erregungsreinheit
:
, 
sind die Farbigkeits-Koordinaten der Grenz-Farbreize.
Es besteht eine gewisse Korrelation mit der empfundenen Sättigung.
Die Bedeutung der Symbole ist die selbe wie in der vorherigen Definition.
bedeutet einfach dessen Reduktion um einen
anderen Stimulus, dessen Tristimulus-Werte das -fache der
ursprünglichen Werte betragen. Es wird gefordert, daß keine
additive Mischung einer reellen Farbe mit irgendeinem anderen
Farbreiz den Null-Farben-Reiz (null color stimulus) ergibt,
d.h. den Reiz, bei dem alle Tristimulus-Werte Null betragen.
Die Ergebnisse der Farbmessung sollen vor allem für normalsichtige Trichromaten gültig sein. Der dabei zugrundegelegte ideale trichromatische Beobachter verhält sich strikt nach den Regeln der strengen trichromatischen Generalisierung (stronger trichromatic generalization), d.h. die oben genannten Gesetze der additiven Farbmischung gelten; außerdem gilt für die Farbmatches das Prinzip der Persistenz der Farbmatches ohne Einschränkung für alle Stimuli.
Die Spezifizierung des idealen Beobachters zur Verwendung in der
Farbmetrik und Photometrik ist Aufgabe der Commission
Internationale de l'Eclairage (oder CIE). Seit 1931 wurde von
dieser Institution der Standardbeobachter festgelegt: Die
farb-matchenden Funktionen 
,
und 
wurden definiert
als Wellenlängen im Bereich von = 380 bis 780 nm in
Intervallen von 
= 5 nm. Bei den neueren
CIE-Empfehlungen von 1971 wurde der Bereich noch etwas ausgedehnt
( = 360 bis 830 nm) und enthält interpolierte Werte in
Intervallen von 1 nm Breite; außerdem wurde die Genauigkeit von 4
auf 7 Stellen erhöht. Die Empfehlungen gelten für Feldgrößen
von 1 bis 4 Grad Sehwinkel.
1964 wurde zur Ergänzung eine weitere farb-matchende Funktion
eingeführt, die für größere Felder genauere Werte liefern
soll; sie wird als 
,
und 
dargestellt. Diese Funktionen sollen verwendet werden, wenn
große Flächen von Farben beurteilt werden sollen; für die
empirische Erhebung der Funktionen wurden Reize, die die zentralen 10
Grad des Sehwinkels ausfüllten, verwendet. Bei einem Feld mit
Sehwinkel Ausdehnung ist das Farbenabgleichen etwa zwei
bis drei mal so
präzise wie bei einem Feld von 
. Die von diesen Funktionen
getroffenen Vorhersagen sind bei großen Flächen und geringer
Beleuchtung nicht ganz korrekt, da dann das skotopische Sehen eine
zunehmende Rolle spielt; hierbei spricht man auch von rod
intrusion.
Manche gleichmäßigen Frabstimuli, die eine große Fläche
einnehmen, erscheinen dem Betrachter nicht gleichmäßig, es tritt
ein sog. Maxwel spot auf, der eine unklare Grenze besitzt und
1 bis 4 Grad einnimmt. Er befindet sich im Mittelpunkt der
Betrachtung und wandert bei Augenbewegung mit. Ursache ist das gelbe
Farbpigment (macular pigment), das die retinalen Rezeptoren
in der fovea centralis bedeckt. Bei der Erstellung der
standard-farbmatchenden Funktionen ,
und wurde
der Maxwell-Spot ausgeschlossen oder ignoriert.
Die Empfehlungen berücksichtigen außerdem das Gesetz der
Additivität für Helligkeiten, das bei normalsichtigen
Beobachtern gilt. Dabei wird gefordert, daß für einen Match
bezüglich der Helligkeit (nicht unbedingt der Farbe) von zwei
relativen spektralen Verteilungsfunktionen 
und 
gilt:
wobei 
eine Funktion der Wellenlänge ist, die als
photopic luminous efficiency function bekannt ist.
Das trichromtische System, das auf den Primärreizen R, G
und B basiert, weist gewisse Nachteile auf, wie z.B. negative
Werte der Farbkoordinaten 
, 
und
; außerdem erfordert die Bestimmung photometrischer
Quantitäten (wie beispielsweise der Leuchtdichte (luminance))
entweder eine weitere Integrierung unter Verwendung der
-Funktion oder die Berechnung einer Linearkombination
der zuvor berechneten Tristimulus-Werte. Deshalb wurde eine
Transformation des trichromatischen Systems, das auf den
Primärreizen R, G und B basiert, zu einem System,
das auf den neuen Primärreizen X, Y und Z basiert,
eingeführt. Die X, Y, Z -Primärreize sind
nichtreal oder imaginär (d.h. sie können nicht durch reale
Farbreize realisiert werden). Im Farbigkeits-Diagramm (
chromaticity diagram) liegen die sie repräsentierenden Punkte
außerhalb des Farbigkeits-Gebietes, das von den Spektrumsgrenzen
und der Violett-Linie abgegrenzt wird. Das Dreieck, das von den
Farbigkeits-Werten X, Y und Z gebildet wird,
enthält die Grenzen des Spektrums und die Violettlinie komplett.
Deshalb sind die Farbigkeits-Koordinaten x, y, z aller realen Farbreize
niemals negativ. Nach folgenden Transformations-Gleichungen lassen
sich die Werte der beiden Systeme ineinander umformen:
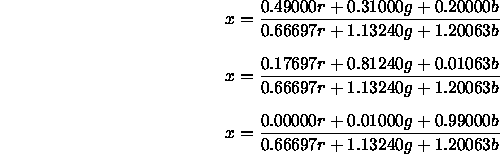
Aus den Farbigkeitskoordinaten x, y, z lassen sich die Tristimulus-Werte X, Y, Z folgendermaßen berechnen:
wobei V die Leuchtdichte des Reizes ist, die entsprechend der
Leucht-Effizienz-Funktion berechnet wurde. Die
Berechnung der farbmatchenden Funktionen erfolgt analog:
Eine weitere Besonderheit der X, Y, Z Primästimuli ist, daß die X und Z Primärreize auf der sogenanten Alynche liegen, die im Farbigkeits-Diagramm eine gerade Linie darstellt, auf der die Farbigkeitspunkte aller Stimuli liegen, die Null Leuchtdichte besitzen.
Für die industrielle Farbmessung ist vor allem die
Farbbeschaffenheit von Objekten interessant. Von einer
Strahlungsquelle ausgehendes Licht trifft auf das Objekt und wird dort
reflektiert. Dem Farbreiz Q mit der spektralen Verteilungsfunktion
, der von einem Objekt ausgeht und in das
Auge des Beobachters tritt, entspricht die relative spektrale
Verteilungsfunktion 
, wobei
die spektrale Konzentration der auf das Objekt
fallenden Strahlungsenergie bezeichnet und 
die
spektralen Reflektionseigenschaften des Objektes bezeichnet. Immer,
wenn vor allem die Farbe von Objekten interessiert, sollte sich die
Farbmessung auf einige wenige spezifische und wohldefinierte spektrale
Verteilungen 
von Strahlungsenergie, die
auf das Objekt fällt, beschränken. Die derartige, von der CIE
empfohlene Menge von spektralen Strahlungsenergie-Verteilungen wird
CIE Standard Beleuchtungen (CIE standard illuminants) genannt.
Sie werden in arbiträren Einheiten angegeben; deshalb handelt es
sich immer um relative spektrale Strahlungsverteilungen.
Folgende Standardbeleuchtungen wurden definiert:
läßt sich mit Hilfe der
Plank'schen Strahlungsformel
berechnen.
.
und D 
,
die für andere Tageslichtbedingungen verwendet werden können.
Die gerade beschriebenen Beleuchtungen (illuminants) beziehen sich auf bestimmte spezifische spektrale Verteilungen der Strahlungsenergie, die auf das beleuchtete Objekt fallen. Eine Leuchtquelle (source) bezeichnet dagegen eine physikalische Quelle von Strahlungsenergie, wie z.B. eine Lampe oder die Sonne. Die CIE empfiehlt folgende Quellen als Standardleuchtquellen, um unter Laborbedingungen farbige Materialien beurteilen zu können:
Zur Messung des Reflektanzfaktors empfiehlt die CIE den perfekt reflektierenden Streuer (perfect reflecting diffuser), der als idealer gleichförmiger Streuer mit einer Reflektanz nahe dem Einheitswert definiert ist. Zur Messung des Reflektanz-Faktors liegen ebenfalls standardisierte Beleuchtungs- und Beobachtungsbedingungen vor (es werden die Winkel, in denen die Beleuchtung einfällt und in denen auf die Probe geblickt wird, definiert).
Die Berechnung der CIE Tristimulus-Werte (hier nach dem System von 1931) geschieht nach folgenden Gleichungen:
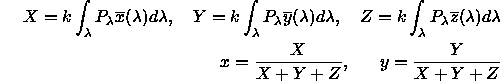
wobei die farbmatchenden Funktionen ,
und den CIE
Standard-Beobachter definieren; 
bezeichnet die
monochromatische Komponente der Wellenlänge 
des gegebenen
Farbreizes mit der spektralen Strahlungsverteilung
; der Faktor k ist ein beliebig wählbarer
Normierungsfaktor. Die Grenzen der Integrale sind gegeben durch
= 360 nm und 
= 830 nm; in der Praxis
werden die Integrale aber durch Summen ersetzt (der Frequenzbereich
wird in gleich breite Abschnitte unterteilt).
Das farbmetrische System der CIE beinhaltet auch Algorithmen zur
Vorhersage der Größe wahrgenommener Farbunterschiede zwischen
zwei Reizen, die sich in ihrer Farbe unterscheiden. Dazu werden zwei
annähernd gleichförmige Farbräume, der 
- und der
-Raum und die damit assoziierte Formeln für
Farbunterschiede empfohlen. Bei der praktischen Anwendung von Formeln
zu Farbunterschieden wird oft gewünscht, daß sich die
Komponenten der Farbunterschiede als Korrelate von Helligkeit,
Sättigung und Farbton identifizieren lassen. Auch hierfür sind
Formeln vorhanden.
Je größer die spektralen Unterschiede zwischen zwei Reizen, die
unter bestimmten Beleuchtungs- und Beobachtungsbedingungen für
gleich gehalten werden, desto deutlicher wird der Mismatch, wenn die
Randbedingungen verändert werden. Daraus ergibt sich das
Konzept des Grades an Gleichfarbigkeit (metamerism). Ein
niedriger Grad an Metamerismus stellt sicher, daß die
Farbüberreinstimmung gegenüber Veränderungen der Beleuchtung
oder des Beobachters invariant ist. Dazu wurde der CIE special
metamerism index entwickelt. Der Grad an Metamerismus M von
zwei Objekten 
und
, die in ihrer Farbe unter bestimmten
Beleuchtungsbedingungen 
für den gegebenen
Beobachter [ , ,
] übereinstimmen, wird in Begrifen der
beobachteten Farbdifferenz 
gemessen, die zwischen den zwei
Objekten unter der anderen Beleuchtungsbedingung
beobachtet wird. Der Grad an Metamerismus
kann dabei stark variieren, je nachdem, welche Testbeleuchtung
verwendet wird; deshalb sollten verschiedene Tests durchgeführt
werden (mindestens zwei).
Color Rendering einer Lichtquelle ist der Effekt dieser Lichtquelle auf die Farberscheinung von Objekten im Vergleich mit deren Erscheinung unter einer Referenzbeleuchtung. Der color rendering index einer Lichtquelle gibt an, wie stark unter spezifizierten Bedingungen die wahrgenommenen Farben des Objektes mit denen bei Beleuchtung durch eine Standardlichtquelle übereinstimmen.
Die Leucht-Wirksamkeit (luminous efficiency), das Verhältnis der Leuchtenergie zum Strahlungsfluß (Einheit: lumen pro Watt), von Farbreizen mit unterschielicher spektraler Strahlungsverteilung, die einige Farbwerte gemeinsam haben, variiert stark. Die Leucht-Wirksamkeit für einen bestimmten Farbwert ist maximal für einen Farbreiz, der aus der geeigneten Mischung eines bestimmten Paares monochromatischer Stimuli besteht.
Objekt-Farbreize (object-color stimuli) sind Farbreize, die
sich daraus ergeben, daß Licht von einem Objekt reflektiert wird.
Dabei ist die spektrale Reflektanzfunktion 
des Objekts
wichtig. Aus allen möglichen Objekt-Farbreizen (d.h. allen denkbaren
Funktionen ) läßt sich der sog.
Objekt-Farbkörper (object-color solid), ein Teil des
Tristimulus-Raumes, definieren. Durch Veränderung der Energie des
einfallenden Lichtes (bei gleicher spektraler Verteilung) läßt
sich der Objekt-Farbkörper herauf- oder herabskalieren. Jeder Punkt
auf der Oberfläche des Objekt-Farbkörpers repräsentiert einen
optimalen Farbreiz, d.h. einen Objekt-Farbreiz, der für
einen gegebenen Farbwert die höchste Leuchtreflektanz (luminous
reflectance) besitzt.
Folgende Begriffe werden zur Beschreibung bestimmter Eigenschaften von Lichtquellen verwendet:
:
Dabei sind 
und 
Konstanten, die von der Lampe
abhängen (typische Werte sind 
und 
).
Metamere Farbreize (Metamere) sind Farbreize mit den selben
Tristimulus-Werten, aber unterschiedlichen spektralen
Strahlungsverteilungen; sie sehen für den Beobachter gleich aus.
Zwei Metamere mit den jeweiligen spektralen Strahlungsverteilungen
und 
müssen
folgende Gleichungen erfüllen:
Die Integrale lassen sich wieder durch Summen annähern:
Bei den hier aufgeführten drei Gleichungen definieren die spektralen
Strahlungsverteilungen
und
ein Paar von
Metameren mit den spektralen Reflektanzfunktionen 
und 
. 
und 
sind
die relativen Strahlstärken bei der Wellenlänge der
Beleuchtungen der beiden Objekte; meist sind sie gleich.
Zur Berechnung von Metameren stehen verschiedene Methoden zur Verfügung (cf. Wyszecki and Stiles, pp. 187 ff):
Die spektralen Reflektanzkurven von metameren Objektreizen
müssen sich jeweils an mindesten drei Stellen innerhalb des
sichtbaren Spektrums überschneiden: Ein Schnittpunkt am kurzen Ende,
einer in der Mitte und einer am langen Ende. Die Regeln, nach denen
die Schnittpunkte bestimmt werden können, sind sehr kompliziert;
bereits die Bestimmung der Anzahl der Schnittpunkte ist nicht einfach
und hängt von der Wahl des trichromatischen Systems (z.B. CIE) ab.
Nach einer Studie von Thornton (1973) befindet sich der Ort der
Schnittstellen bei Wellenlängen von 448 
4 nm, 537 3 nm,
und 612 8 nm; andere Autoren konnten aber zeigen, daß der
Ort der Schnittpunkte stark von der Methode der Erzeugung der Metamere
abhängt.
Zu jedem Punkt auf der Oberfläche des Objekt-Farbenkörpers gibt es genau einen Objekt-Farbreiz und keine Metamere. Für jeden Punkt innerhalb des Objekt-Farbenkörpers gibt es dagegen unendlich viele Metamere. Die größte Häufigkeit tritt dabei in der zentralen Zelle des Objekt-Farbkörpers (chromaticity point) auf.
Eine interessante Frage ist die nach den Grenzen, außerhalb derer bei der Beurteilung von zwei Metameren keine Farbübereinstimmung mehr beobachtet wird, wenn Beleuchtung oder Beobachter ausgetauscht werden. Zur Bestimmung der Grenzen der Punktewolke im (X, Y, Z)-Tristimulus-Raum liegen verschiedene Untersuchungen vor; dabei wurde jeweils die Beleuchtung verändert, nicht der Beobachter (die Berechnungen wären aber analog). Wyszecki und Stiles (1982, pp. 201ff) führen folgende Methoden auf:
Gestalt und Umfang der Grenzen hängen von den Tristimulus-Referenzwerten ab: Die Punktewolke schrumpft, wenn sich der entsprechende Referenzpunkt der Metamere zu den Grenzen des Objekt-Farbkörpers hin bewegt.
Ein Spektroradiometer dient zur Messung radiometrischer Quantitäten als Funktion der Wellenlänge. Meist erfolgt die Messung durch Vergleich der Testquelle mit einer geeigneten Referenzquelle bekannter spektraler Strahlungsverteilung. Die Messung erfolgt nicht für jede einzelne Wellenlänge, sondern als mittlere spektrale Energieverteilung eines zusammenhängenden Bereichs an Wellenlängen von kleiner, endlicher Breite.
Spektrophotometer dienen zur Messung der spektralen Durchlässingkeit (spectral transmittance) und der spektralen Reflektanz von Objekten. Zweck ist, für jede Wellenlänge die Strahlungsenergie, die das Objekt verläßt, mit derjenigen zu vergleichen, die auf das Objekt auftrifft.
Das Phänomen der Fluoreszenz gehört zu den Phänomenen der Lumineszenz, also zu den Prozessen, bei denen Moleküle oder Atome durch die Absorption von Strahlungseneergie in einen Erregungszustand versetzt wurden. Die relative spektrale Strahlungsverteilung der abgegebenen Strahlung beschreibt den speziellen Charakter der Fluoreszenz; eine Veränderung der Wellenlänge der eintreffenden Strahlung führt nicht zu einer Änderung des Spektrums der abgegebenen Strahlung, nur zu einer Veränderung der Strahlungsenergie. Bei der spektrophotometrischen Analyse von fluoreszierendem Material geht es darum, den gesamten spektralen Strahlungsfaktor des Materials zu bestimmen, der sich additiv aus einer Komponente der Reflexion alleine und einer Komponente der Fluoreszenz alleine zusammensetzt (das Ergebnis hängt allerdings auch von der Leuchtquelle, mit der das Objekt bestrahlt wurde, ab). Die zur Messung der einzelnen Komponenten nötigen Aufbauten werden von Wyszecki and Stiles (1982, pp. 235ff.) beschrieben.
Tristimulus-Filter-Farbmessgeräte (tristimulus-filter
colorimeters) sind Instrumente mit einer spektralen
Antwortfunktion, die direkt proportional ist zu den farbmatchenden
Funktionen eines der CIE-Standardbeobachter. Die kommerziell
erhältlichen Geräte dieser Art sind allerdings oft ungenau.
Hauptproblem bei der Konstruktion solcher Geräte ist es, drei
Photozellen so einzustellen, daß ihre Antwort-Funktionen über das
gesamte sichtbare Spektrum hinweg proportional zu den farbmatchenden
Funktionen eines der CIE-Standardbeobachter sind. Eine Methode besteht
darin, für jeden der drei Photorezeptoren mit einem Monochromator
und einer Spektrums-Schablone die gewünschten spektralen
Antwort-Funktionen , ,
einzustellen; das Ergebnis ist ein sogenannter
template colorimeter. Die Spektrumsschablonen sind so
beschaffen, daß sie selektiv ein Spektrum gleicher Energie so
modifizieren, daß die spektrale Reaktionskurve des Photorezeptors
jeweils die Form einer der drei farbmatchenden Kurven des
Standardbeobachters annimmt.
Bei der zweiten Methode wird die spektrale Antwortfunktion der Photorezeptoren
durch spezielle Filter abgeändert; man erhält dann einen sog.
filter-photocell colorimeter.
Folgende Begriffe der Photometrie sind nach Wyszecki and Stiles (1982, pp. 787 f.) wichtig (die genannten Begrife beziehen sich auf photopisches Sehen):
, 
repräsentiert die Leuchteffizienz eines monochromatischen
Strahlenflußes der Wellenlänge . repräsentiert die maximale Leuchteffizienz eines
monochromatischen Strahlenflußes, der bei der Wellenlänge
, bei der 
gilt, erhalten
wird; entspricht 683 lumen pro Watt.
(auch photopic
luminous efficiency function) bezeichnet das Verhältnis des
Strahlenflußes bei der Wellenlänge 
nm (bei
der der maximale Wert dieses Verhältnisses 1 ergibt) zu der
Wellenlänge , wenn diese beiden Strahlungsflüsse unter
spezifizierten Bedingungen zu der selben photopischen
Beleuchtungsempfindung führen.
(auch scotopic
luminous efficiency function) bezeichnet das Verhältnis des
Strahlenflußes bei der Wellenlänge 
nm (bei
der der maximale Wert dieses Verhältnisses 1 ergibt) zu der
Wellenlänge , wenn diese beiden Strahlungsflüsse unter
spezifizierten Bedingungen zu der selben skotopischen
Beleuchtungsempfindung führen.
oder Leuchtenergie, 
(oder 
) mit der
Einheit lumen und dem Strahlungsfluß beim
photopischen Sehen:
Hier ist 
der in dem Wellenbereich 
ausgesandte Strahlungsfluß und ist die photopische
Leuchteffizienz-Funktion. Der Faktor ist die maximale
Leuchteffizienz, die der Wellenlänge entspricht, bei der .
m 
.
m .
m .
Die grundlegende Operation in der Photometrie ist das Matchen von Helligkeiten: Die visuellen Stimuli (zwei nebeneinander liegende Lichtflecken von gleicher Gestalt und Größe) sollen so eingestellt werden, daß deren Helligkeit gleich erscheint. Interessant werden solche Vergleiche, wenn sich die den Lichtreizen zugrunde liegende spektrale Verteilungsfunktion bei den beiden Reizen unterscheidet (heterochromatisches Helligkeits-Matching). Ein Helligkeitsabgleich zwischen zwei Farben kann immer erreicht werden durch Variation des absoluten Wertes eines Reizes.
Heterochromatisches Helligkeits-Matching im direkten Vergleich fällt den Beobachtern schwer, da für die Beurteilung einer Quantität (Helligkeit) auch zwei andere Quantitäten (Farbton und Sättigung) herangezogen werden müssen. Deshalb werden meist indirekte Methoden verwendet (Flimmerverschmelzungs-Methode oder Schritt-für-Schritt-Methode).
Es wird davon ausgegangen, daß für Helligkeitsvergleiche die
selben Gesetzmäßigkeiten gelten wie für Farbvergleiche (siehe
oben): Symmetrie, Transitivität, Proportionalität und
Additivität. Die notwendige und hinreichende Bedingung für einen
Helligkeits-Match zwischen zwei visuellen Reizen mit den spektralen
Helligkeitsfunktionen und
lautet:
wobei 
eine feste Funktion der Wellenlänge ist, die
den Prozeß des Helligkeits-Matches charakterisiert; diese Funktion
unterscheidet sich darin, ob photopisches oder skotopisches Sehen
beschrieben werden soll. Die genannten Gesetze besitzen dann annähernde
Gültigkeit, wenn photopisches Sehen vorliegt und wenn direkt auf
eine senkrecht zur Blickrichtung liegende Fläche geblickt wird
(sonst kann es zu einer Verletzung des Gesetzes der Proportionalität
kommen). Von der CIE wurden zwei Standard photometrische
Beobachter definiert durch 
für
photopisches und 
für skotopisches
Sehen. Ähnliche gleichförmige Lichtflecken, die die durch
und definierten visuellen
Stimuli produzieren, werden genau dann als gleich hell beurteilt,
wenn gilt:
Dies ist gleichbedeutend mit folgender Aussage: Der photopische Leuchtfluß, der in das Auge pro Kegelwinkel eintritt muß für beide Reize gleich sein. Folgende Methoden der Photometrie werden von Wyszecki and Stiles aufgeführt:
-Funktion
annähernd übereinstimmt; dies wird meist durch eine spezielle
Kombination von Absorptionsfiltern erreicht. Der Output solcher
Geräte wird üblicherweise mittels standardisierter
Lampen geeicht.
berechnet wird.
Wyszecki and Stiles (1982, p. 263ff) führen auch Verfahren zur Messung des gesamten Leuchtflusses und der Leuchtintensität und Leuchtdichte auf.
Folgende Prozeduren können für das Matching verwendet werden: Zwei Reize werden als durch strikte Ersetzung visuell äquivalent bezeichnet, wenn ein Stimulus durch den anderen ersetzt werden kann, ohne daß sich das Urteil des Beobachters darüber, was gesehen wurde, ändert; dabei muß die Ersetzung exakt sein (Präsentation auf die gleiche Netzhautstelle usw.). Eine weitere Bedingung ist, daß die beiden Vergleichs-Beobachtungen völlig unabhängig voneinander erhoben werden: Das Urteil soll nicht durch die Möglichkeit eines direkten Vergleichs beeinflußt werden. Das Urteil des Beobachters besteht normalerweise in der Zustimmung oder Ablehnung einer Proposition über eines der gesehenen Merkmale; oft wird das statistische Kriterium ``Zustimmung in mehr als 50% der Fälle'' verwendet. Beim Teststimulus läßt sich die absolute spektrale Verteilung der Strahlungsenergie variieren. Es können aber auch die Polarisation oder die Größe und Gestalt der Eintrittsöffnung ins Auge verändert werden; da meist jedoch Interesse an den Auswirkungen von Veränderungen der spektralen Zusammensetzung der Reize besteht, werden die anderen Bedingungen konstant gehalten. Als Reize werden meist gleichmäßige Lichtflecken verwendet ( uniform light patches); manchmal werden aber auch komplexere Reize verwendet (siehe unten).
Gilt die Äuquivalenz zweier Reize A und B, dann besitzt die
dazugehörige Äquivalenzrelation 
folgende Eigenschaften:
.
Ob die Elemente der Äquivalenzklassen eine Form der Linearität erfüllen, läßt sich nur empirisch entscheiden. Dazu müßten folgende Bedingungen erfüllt sein:
, dann 
, wobei 
ein
beliebiger positiver Faktor ist; und 
impliziert die andere.
Eine eingeschränktere Form der Linearität gilt dann, wenn für
die drei Stimuli A, B und 
, wobei 
, gilt: Die Äquivalenz von zweien impliziert die Äquivalenz
aller drei.
Der Vergleich zweier Reize, bei denen die Darbietungssituation nicht völlig gleich ist, wird als asymmetrisch bezeichnet. Dies ist beispielsweise in folgenden Situationen der Fall:
Unter folgenden Bedingungen der asymmetrischen Äquivalenz ist asymmetrisches Matching möglich:
Jede mögliche Kombination von Testreizen und Darstellungssituationen, die die vorgeschriebenen Propositionen erfüllt, ist Mitglied einer Äquivalenzklasse von (Stimulus/Display)-Kombinationen. Die Testreize von zwei beliebigen Mitgliedern solcher Äquivalenzklassen repräsentieren einen indirekten asymmetrischen Match, der symbolisch folgendermaßen repräsentiert wird:
(A/ds: x) - iam: k - (B/ds: y),
wobei
stimulus A
stimulus B
Display-Situation x
Display-Situation y
indirekter asymmetrischer Match mit
Erscheinungskriterium k.
Die durch das Symbol ``iam: k'' bezeichnete Relation ist reflexiv und transitiv, aber bei einem Tausch der Testreize nicht unbedingt symmetrisch. Die gerade definierte Äquivalenzklasse besteht aus Subklassen, bei denen die Darstellungssituation gleich ist und nur der Teststimulus variiert wird.
Im Gegensatz zu indirekten asymmetrischen Matches wird bei direkten asymmetrischen Vergleichen von einem Beobachter die Übereinstimung zweier gleichzeitig präsentierter Reize beurteilt. Wenn ``dam: k'' als Abkürzung für ``matcht im direkten asymmetrischen Vergleich mit Kriterium k'' verwendet wird, dann läßt sich der Match symbolisch folgendermaßen ausdrücken:
(A/ds: x) - dam: k - (B/ds: y),
wobei k ein Gleichheitskriterium sein muß. In diesem Fall gilt auch die Symmetrie. Das Kriterium für Gleichheit bei direktem asymmetrischen Matching soll auch ein streng vergleichendes Beurteilen des Aussehens zweier Reize ermöglichen, das sich nicht in zwei Urteile trennen läßt, von denen sich jedes nur auf das Erscheinen eines Testreizes bezieht: Das Kriterium der Gleichheit muß nonseparabel sein.
Wenn davon ausgegangen werden kann, daß zwei Testreize, die asymmetrisch übereinstimmen, auch übereinstimmen würden, wenn der selbe Vergleich (mit vergleichbarer Präzision) durch eine streng symmetrische Ersetzungsprozedur erfolgen würde, nennt man die asymmetrische Prozedur auch quasi-symmetrisch. Quasi-symmetrisches Matching ist zu erwarten, wenn folgende Bedingungen erfüllt sind:
Bei Vergleichsprozeduren, bei denen die Asymmetrie ein wesentliches Element des Vergleiches darstellt, spricht man von spezifisch asymmetrischen Vergleichen.
Die Match-Kriterien, nach denen eine Beurteilung der Übereinstimmung gegeben werden soll, unterscheiden sich in ihrer Komplexität stark. Das einfachste und häufigste Kriterium ist der vollständige Farbmatch, bei dem Helligkeit, Farbton und Sättigung übereinstimmen müssen. Folgende Formen des unvollständigen Farbmatches sind prinzipiell möglich:
Hierbei kommen unterschiedliche Forschungsmethoden zum Einsatz; in der Praxis vor allem die erste Form verwendet:
Folgende Matching-Prozeduren werden von Wyszecki and Stiles (1982, pp. 288ff.) aufgeführt:
Bei gegebener Darbietungssituation, gegebenem Matching-Kriterium und dem Vergleichsreiz C entspricht die retinale Reaktion der Fläche, auf die der Reiz abgebildet wird, der Maxwell'schen Trichromatizität / C, wenn folgende drei Bedingungen erfüllt sind:
,
und , die Primärmenge, finden, so daß
ein Teststimulus, der aus Mischungen der Strahlungsenergie (> 0) 
von , 
von , und 
von
besteht, den Vergleichsstimulus C matcht. Diese
Mischung ist eindeutig, d.h. keine andere Mischung der Primärmenge
matcht C. ,
und , für die Bedingung (1) gilt,
läßt sich eine eindeutige Mischung aus geeigneten
Strahlungsenergien 
und höchstens zwei weiteren
Wellenlängen der Primärmenge finden, die den Reiz C matcht.
für alle
Wellenlängen (wobei ), dann gilt: Wenn
zwei Reize von P, P', P'' mit C matchen, dann tut es auch der
dritte (Additivitätsgesetz für Maxwell'sches Matching).
Das Auge scheint bei der Wahrnehmung von Lichtreizen nur drei verschiedene unabhängige Quantitäten zu verarbeiten (auch wenn diese aus der Zusammenschaltung der Reaktionen aus mehr als drei Systemen mit linear unabhängigen spektralen Empfindlichkeiten resultieren); in der inneren extrafovealen Region befinden sich beispielsweise vier Arten von Rezeptoren: drei Zäpfchensysteme und ein Stäbchensystem.
Maxwell'sche N-Chromatizität / C gilt dann, wenn N
Farbsysteme zum Einsatz kommen; Matchen des Reizes C und Erfüllen
der allgemeinen Matchbedingung (siehe unten) sind äquivalente
Aussagen über den Teststimulus P mit der absoluten spektralen
Strahlungsverteilung 
. Die allgemeine Matchbedingung lautet
folgendermaßen:
wobei 
die N linear unabhängigen
farbmatchenden Funktionen sind und 
die Komponenten des
entsprechenden N-Stimulus-Vektor 
für den Testreiz P;
sind die Komponenten des N-Stimulus-Vektor 
,
der dem Vergleichsstimulus C entspricht.
In der Matrixschreibweise lassen sich die N farbmatchenden
Funktionen als Zeilen der 
farbmatchenden Matrix schreiben; der Testreizvektor P ist eine
-Spaltenmatrix und und sind 
Spaltenmatrizen. Zwei farbmatchende Matrizen 
und
werden als äquivalent bezeichnet, wenn sie sich durch eine
nichtsinguläre 
Matrix T ineinander überführen
lassen, so daß
Die Präzision, mit der sich Farbmatches herstellen lassen, hängt
von der jeweiligen Farbe ab; die ersten systematischen Untersuchungen
in dieser Richtung wurden von MacAdam (1942) durchgeführt. Der Beobachter
konnte durch Drehen eines Knopfes die Farbe einer Hälfte eines
Feldes entlang einer geraden Linie im CIE-Farbigkeitsdiagramm
variieren, wobei die Leuchtdichte automatisch konstant gehalten wurde.
Das Feld war von einem 
Feld umgeben, das in seiner
Farbigkeit etwa der Standardleuchtquelle C entsprach. Sowohl der
variable als auch der feste Reiz bestanden aus Mischungen der selben
Menge an Primärfarben rot, grün und blau. Zwischen dem variablen
Stimulus und dem festen Reiz wurden wiederholt Farbabgleiche
durchgeführt.
Die Standardabweichungen der Abweichung zwischen dem
Farbigkeitspunkt des variablen und des festen Reizes wurden bestimmt.
In zusätzlichen Experimenten fand MacAdam heraus, daß gerade
eben merkliche Farbunterschiede etwa drei mal so große
Abweichungen erfordern wie die oben erhaltenen Standardabweichungen.
Für den variablen Stimulus wurden verschiedene gerade Linien, die
sich alle an einem Farbigkeitspunkt schnitten, verwendet. Die
resultierenden Standardabweichungen der Farbmatches wurden als
Distanzen 
entlang dieser Linien geplottet, gemessen von dem
zentralen Farbigkeitspunkt 
aus. Die empirisch so
erhaltenen Endpunkte fielen auf eine Ellipse, deren Größe, Form
und Orientierung sich veränderte, wenn ein andere Farbigkeits-Punkt
verwendet wurde. Die Ellipsen, die bekannte Standardabweichungen beim
Farbmatchen darstellen, werden MacAdam Ellipsen genannt; sie
können durch folgende Gleichung beschrieben werden:
wobei dx bzw. dy den Abstand der x- bzw. y-Koordinate vom
Ursprung bezeichnen. Wenn 
den Winkel der
Hauptachse der Ellipse zur x-Achse des Koordinatensystems
bezeichnet, lassen sich die 
folgendermaßen berechnen:
Die Formeln zur Berechnung der inversen Werte sind in Wyszecki and
Stiles (1982, p. 307) zu finden. Die Werte der einzelnen
unterscheiden sich systematisch von einer Ellipse zur nächsten.
Durch Interpolation lassen sich auch die dazwischenliegenden Werte
feststellen uns somit ``glatte'' Konturlinien herleiten.
Aus den gegebenen Koeffizienten 
, 
, 
als
Funktion von x und y läßt sich eine Oberfläche in einem
gewöhnlichen dreidimensionalen euklidischen Raum definieren, auf der
alle Reize mit konstanter Leuchtdichte in einem MacAdam-Plot als
Punkte dargestellt werden. Wenn die Distanz zwischen zwei Punkten auf
der Oberfläche einen gewissen kleinen Wert besitzt, sind die
entsprechenden Reize eben unterscheidbar. Auf dieser Oberfläche
zeichnen sich die MacAdam-Ellipsen als Kreise identischer
Größe; die Oberfläche kann deshalb als Oberfläche der
gleichförmigen Farbigkeitsskala (
uniform-chromaticity-scale surface) beschrieben werden.
Die Beschränkung auf Farben gleicher Leuchtdichte wurde bei der Bestimmung des trichromatischen Farbmatchens von Brown und MacAdam (1949), bei der Erstellung der Brown-MacAdam Ellipsoide fallengelassen. Die Beobachter konnten die Beträge aller drei Primärfarben variieren (unter ähnlichen Bedingungen wie bei MacAdam). Brown stellte auch fest, daß die Farbe des die Stimuli umgebenden Feldes einen deutlichen Einfluß auf die Genauigkeit des Farbmatches bewirkt: Bei geringen Farbunterschieden fällt die Entdeckung schwerer, wenn das umgebende Feld eine andere Farbigkeit aufweist. Auch die Orientierung und Form der Ellipsoide wird durch die Farbe der umgebenden Felder beeinflußt.
Bei Verwendung des 7-Feld binokularen Farbmessgerätes von Wyszecki und Fielder (1971) (wobei alle außer zwei gegenüberliegenden Feldern durch weiße Umgebung ersetzt wurden) erhält man Wyszecki-Fielder Ellipsoide. Diese Beobachtungsbedingungen ähneln dem ``normalen'' Sehen am meisten.
Es zeigen sich öfter größere Unterschiede zwischen den Ellipsen, die man von den selben Beobachtern zu unterschiedlichen Zeitpunkten unter ansonsten identischen Bedingungen erhält. Die empirisch erhaltenen Unterschiede sind wesentlich größer als die statistisch zu erwartenden Schwankungen; deshalb ist zweifelhaft, ob die klassischen statistischen Techniken überhaupt auf visuelle Daten der genannten Art anwendbar sind.
Werden verschiedene Beobachter miteinander verglichen, stimmen die Ellipsen für einzelne Punkte des Farbigkeits-Diagramms nicht überein: Es zeigen sich deutliche Unterschiede in Größe, Form und Orientierung der Ellipsoide. Ein Teil dieser Unterschiede resultiert wohl aus den Unterschieden, die auch bei einem einzelnen Beobachter zu verschiedenen Zeitpunkten auftreten würden. Die restlichen Unterschiede müssen anderen Gründen zugeschrieben werden, wie z.B. unterschiedlichen Beobachtungsbedingungen oder unterschiedlichen visuellen Mechanismen. Zwischen den verschiedenen Beobachtern stimmt die Orientierung der Ellipsen relativ gut überein; auch die Größe der Ellipsen variiert nicht zu stark. Größere Unterschiede treten dagegen bei der Form der Ellipse (dem Verhältnis a/b) auf.
Von Guild (1931) und Wright (1928-1929) stammen die experimentellen
Daten, aus denen zusammen mit der CIE 1924 Leuchteffizienzfunktion
die Grundlagen für die farbmatchenden Funktionen des
CIE 1931 Standard-Farbmatchenden Beobachters gewonnen wurden. Judd
(1951) führte noch eine Anpassung dieser Funktion ein, so daß
die Werte im Bereich der Wellenlängen unter 460 nm gegenüber dem
CIE 1931-Schema genauer werden. Vos (1978) konnte diese Funktion noch
etwas genauer machen.
Stiles führte in den 50er Jahren ein Neubetrachtung der CIE-Daten durch, da Probleme in folgenden Bereichen vermutet wurden:
im Bereich des blauen Endes des Spektrums;
Nach Vorversuchen mit 10 Versuchspersonen kam das CIE-Kommittee zu dem
Schluß, daß die CIE 1931 Daten für Sehfeld genau
genug seien, aber für 
Sehfeld überarbeitet werden
müßten. Daraus folgte die Entwicklung des CIE
1964-Ergänzungsschemas; die Daten dafür wurden von Stiles und
Burch (1959) an 49 Beobachtern erhoben.
Zum Matching durch Erstellung einer additiven Mischung von Farben sind drei verschiedene Farben notwendig (bzw. drei Arten von Filter-Pigment-Kombinationen / Zäpfchen). Der Begriff color gamut bezeichnet die Menge derjenigen Farben, die sich dann auch tatsächlich durch Mischen der drei Primärfarben erzeugen lassen; dessen ``Geltungsbereich'' hängt natürlich von der Wahl der Primärfarben ab.
Eine durch auftreffende Lichtstrahlen beleuchtete Fläche erscheint dann selbstleuchtend, wenn sie durch ein Loch in einer Trennwand, die davor plaziert ist, betrachtet wird, wobei diese Trennwand dunkler sein muß als der betrachtete Testreiz. Wird die Trennwand dagegen beleuchtet, so erscheint der Testreiz dann nicht mehr selbstleuchtend, wenn die Helligkeit des ``Kontextes'' höher als die des Reizes ist (Wechsel vom self-luminous mode zum object-color mode).
Das Gesetz von der Persistenz von Farbmatches (nach Kries, 1905) besagt, daß Farbmatches unter verschiedenen Kontexten erhalten bleiben; es verliert seine Gültigkeit allerdings bei sehr hohen Helligkeiten und bei sehr großflächigen Reizen (größer als 2° Sehwinkel, also Beteiligung der Stäbchen).
Einheiten der einen Farbe gleichfarbig mit Einheiten der anderen Farbe (Proportionalität).
Die ersten beiden Punkte begründen die Additivität; alle drei zusammen die Linearität.
Der Tristimulus-Farbraum (tristimulus color-space) ist ein Koordinatensystem, das aus den drei Primärfarben Rot (R), Grün (G) und Blau (B) besteht; jeder der drei Farben entspricht dabei ein Achse. Diese Achsen besitzen einen gemeinsamen Ursprung und dürfen nicht alle in einer Ebene liegen; sie müssen nicht senkrecht aufeinander stehen.
Jeder Farbe (bzw. jedem Farbreiz) S entspricht dann ein Vektor in diesem System. Gleiche Beträge von R, G und B bewirken ein neutrale Farbe N. Die Einheitsebene (unit plane oder auch chromaticity diagram genannt) geht durch die Punkte R = (1, 0, 0), G = (0, 1, 0) und B = (0, 0, 1). Sie läßt sich auch folgendermaßen definieren:
Innerhalb dieses Farbraums kann die Mischung zweier Farben als Vektoraddition betrachtet werden. Der Farbvektor S schneidet (zumindestens dann, wenn er entsprechend verlängert wird) die Einheitsebene; dieser Schnittpunkt S heißt chromaticity point der Farbe S. Der Punkt S besitzt die drei Farbigkeits-Koordinaten r, g und b. Geometrisch lassen sie sich folgendermaßen veranschaulichen: In einem Dreieck, dessen Eckpunkte die Primärreize R, G und B bilden, berechnen sich die Koordinaten folgendermaßen:
Man kann aber auch andere Primärreize als R, G und B verwenden, beispielsweise X, Y und Z. Dann ist folgende Umrechnung erforderlich:
wobei 
die Anteile der jeweiligen Farbe (gemischt aus X, Y, Z) bezeichnet, um einen Match zu der Farbe (R = 1, G = 0, B = 0) herzustellen; 
bezeichnen die Anteile zum Matchen von (R = 0, G = 1, B = 0) und 
bezeichnen die Anteile zum Matchen von (R = 0, G = 0, B = 1).
Diese Transformationsmatrix beschreibt also die Beziehung zwischen zwei Mengen an Primärfarben R, G, B und X, Y, Z eindeutig. Für die Farbigkeitskoordinaten (chromaticity coordinates) läßt sich ebenfalls eine (etwas kompliziertere) Transformation angeben; bei dieser handelt es sich um eine projektive Transformation in der Ebene (diese Ebene ist übrigens das chromaticity diagram).
Somit gilt: Einer linearen Transformation (bzw. einer affinen) des Tristimulus-Raums entspricht eine projektive Transformation der Farbigkeits-Koordinaten.
Ausgangspunkt für die farbmatchenden Funktionen sind die drei Primärstimuli
nm,
nm und
nm.
Ihre Strahldichte (radiance) steht dabei im Verhältnis von 72.1 : 1.4 : 1.0 zueinander (bei diesem Mischungsverhältnis läßt sich ein Match mit einem equal energy stimulus, bei dem alle Wellenlängen zwischen 380 und 770 nm gleich stark vertreten sind, erzielen).
Nun wird versucht, durch eine additive Mischung der Primärfarben (die entsprechend abgeschwächt werden können) einen Match zu einem monochromatischen Reiz zu erstellen (dabei wird ein sog. bipartite visual field von 2° Sehwinkel verwendet). Aus den jeweiligen Intensitäten der drei zu mischenden Farben erhält man nun die neuen Tristimulus-Werte 
.
Variiert man nun über den sichtbaren Wellenlängenbereich für feste Primärfarben, so erhält man die gesuchten spektralen Tristimulus-Werte für konstante Strahldichte.
Die farbmatchenden Funktionen 
ergeben sich aus einer linearen Transformation von ; sie beziehen sich auf die imaginären Primärfarben X, Y, Z, die von der CIE (1931) eingeführt wurden. Diese neuen Funktionen können nur positive Werte annehmen; die Farbigkeits-Koordinaten werden wiederum so nach dem bekannten Schema
berechnet, daß x + y + z = 1. Außerdem wird das chromaticity diagram so gewählt, daß bei Z ein rechter Winkel vorliegt.
Trägt man in dem X-Y-Z-Farbigkeits-Diagramm die monochromatischen Reize von 400 - 700 nm ein, erhält man den parabelförmigen spectrum locus. Die gerade Verbindungslinie zwischen dem Anfangspunkt bei etwa 400 nm und dem Endpunkt bei etwa 700 nm wird auch als die Violettlinie (purple line) bezeichnet, da es sich dabei um eine Mischung aus Blau und Rot handelt. Etwa in der Mitte liegt der equal-energy-stimulus, für den gilt x = y = 1/3 = z; dieser Punkt wird als farblos/weiß wahrgenommen. Außerhalb dieses parabelförmigen Gebildes liegende Farben werden als imaginäre Farben bezeichnet.
Die farbmatchenden Eigenschaften eines einzelnen Beobachters unterscheiden sich von denen des idealen Beobachters aufgrund verschiedener im folgenden betrachteter Faktoren systematisch:
Die gelben Filterpigmente innerhalb des optischen Mediums im Auge wirken nur als Filter zwischen dem externen Stimulus und den Rezeptoren. Die spektralen Dichtefunktionen der Pigmente sind bekannt, so daß deren Effekt auf die Farbigkeit eines weißen Stimulus berechnet werden können. Die Dichte des Linsenpigments nimmt deutlich mit dem Alter zu und führt so zu einer Veränderung der farbmatchenden Funktionen.
Auch das Mitwirken der Stäbchen bei großflächigen
Farbmatches beeinflußt das Farbabgleichen. Das Hinzunehmen des
Stäbchenmechanismus bei Vergleichen größerer Farbflächen
führt in der Praxis nicht dazu, daß für einen Farbmatch die
spektralen Strahlungsenergieverteilungen vier anstelle von drei
Übereinstimmungsbedingungen erfüllen müssen. Wenn die
Helligkeitsadaptation nachläßt, wird die Matching-Prozedur
weniger dreidimensional und eine Dimension genügt schließlich
zum Match mit der skotopischen Leuchteffizienzfunktion .
Folgende Untersuchungen wurden dazu durchgeführt:
,
, und der
skotopischen Leuchteffizienz-Funktion ist so, daß
sich in den Extremfällen die maximale und die minimale spektrale
Energieverteilung auf Mischungen von nur zwei monochromatischen
Komponenten reduziert.
Sehwinkel verwendet werden.
Typischerweise reichen vier Durchläufe dieser Prozedur,
um zu stabilen Werten zu kommen.
Auch der Ort im visuellen Feld spielt eine wichtige Rolle beim Farbmatchen: Wenn das Testfeld von der zentralen Region der fovea centralis wegbewegt wird, stimmt weder die CIE 1931 noch die CIE 1964 farbmatchende Funktion. Peripheres Farbmatchen weicht deutlich vom fovealen oder parafovealen ab; die Abweichungen nehmen mit der Distanz von der fovea centralis zu. Ursache sind neben Unterschieden in der Pigmentierung und Defekten in der Lichtbrechung vor allem Variationen in der neuronalen Topographie.
Werden kleine Testfelder beständig von der peripheren Retina betrachtet, kann lokale Adaptation auftreten; man spricht hier von dem Troxler Effekt. Dieser Effekt tritt in der Peripherie deutlicher auf als in der fovea centralis. Experimentelle Daten deuten darauf hin, daß das trichromatische Sehen der fovea centralis sich für Testfelder mittlerer Größe und bei gegebeber Leuchtdichte und Beobachtungszeit zu dichromatischem Sehen reduziert.
Die Unterschiede aufgrund der Größe des visuellen Feldes resultieren vor allem aus einem Nachlassen der optischen Dichte des okularen Mediums (vor allem des Sehpigmentes). Es werden auch Unterschiede in der Empfindlichkeit des Zäpfchenmechanismus berichtet. Farbvergleiche können bei größeren Flächen präziser durchgeführt werden.
Nach Betrachten eines Reizes von hoher Leuchtdichte verändert sich die Zusammensetzung der Primärfarben, die einen gegebenen Stimulus matchen sollen. Ursache ist möglicherweise das Ausbleichen der Pigmente in der Zäpfchen.
Folgende beiden Methoden des Farbmatchens lassen sich unterscheiden:
Es zeigen sich geringe systematische Unterschiede in der erhaltenen farbmatchenden Funktion je nach der verwendeten Methode des Farbmatchens. Insbesondere scheinen bei der Maxwell'schen Methode etwas größere Unsicherheiten aufzutreten.
Folgende experimentelle Methoden lassen sich zur Bestimung der Farbempfindlichkeitsfunktionen angeben:
Wird ein aus verschiedenen spektralen Strahlungsverteilungen zusammengesetzter Teststimulus in seiner Helligkeit mit einem festen weißen Referenz-Stimulus verglichen, wird die Helligkeit des Teststimulus meist niedriger eingestellt; d.h., der zusammengesetzte Stimulus erscheint heller. Dieses Phänomen wird als Farbenglut oder Helmholtz-Kohlrausch-Effekt bezeichnet. Dieser Effekt wird mit zunehmender Sättigung des Testreizes deutlicher.
Bei den experimentellen Untersuchungen zum heterochromatischen Helligkeits-Matching treten deutliche Verletzungen des Gesetzes der Additivität (Abney's law) auf.
Wird ein achromatischer Stimulus zu einem Farbreiz hinzugemischt, ändert sich im allgemeinen dessen wahrgenommener Farbton. Dieses Phänomen wird als Abney Effekt bezeichnet. Der Effekt der Leuchtdichte auf den wahrgenommenen Farbton wird als Bezold-Brücke Effekt bezeichnet.
Der Begriff Richtungsempfindlichkeit bezieht sich auf Unterschiede aufgrund des Ort des Eintretens der Lichtstrahlen in das Auge (bei Projektion auf die selben Netzhautareale). Je weiter vom Zentrum der Pupille entfernt das Licht eintritt, desto stärker reduziert sich die Reaktion (Stiles-Crawford Effekt erster Ordnung). Es treten nicht nur Unterschiede in der wahrgenommenen Helligkeit auf, sondern auch leichte Änderungen der Farbe ( Stiles-Crawford Effekt zweiter Ordnung).
Die verschiedenen Untersuchungen zur Farbadaptation deuten darauf hin, daß der Vergleich von Reizen in unterschiedlich adaptierten Netzhautarealen dreidimensional ist (d.h. ein zufriedenstellender Match kann durch eine Mischung von drei Primäfarben erzielt werden; zwei reichen dagegen nicht aus). Bei stark unterschiedlichem Adaptationszustand lassen sich einige Reize nicht matchen (analog zu bestimmten sehr gesättigten Farben). Bei einem unterschiedlichem Adaptationszustand spricht man von asymmetrischem Matching.
Nach der von Kries Hypothese verändern unterschiedliche Adaptationszustände bestimmter retinaler Areale die Gesamtempfindlichkeit der drei grundlegenden Farb-Reaktions-Mechanismen. Bei Adaptation an eine hellere Umgebung scheinen Farben eine größere Reinheit zu besitzen. Hunt (1950) bietet dafür folgende Erklärung an: Im dunkeladaptierten Zustand sind die Zäpfchen-Rezeptoren (auch die mit den verschiedenen Farbpigmenten) auf neuronaler Ebene in drei Gruppen verschalten, die die Helligkeit und die Farbigkeit des Testreizes bestimmen. Bei Adaptation an höhere Umgebungsbeleuchtung brechen einige dieser neuronalen Verbindungen zusammen, so daß in zunehmendem Maße die Rezeptoren eines bestimmten Mechanismus nur noch ein Pigment enthalten. Die effektiven spektralen Empfindlichkeitskurven werden enger.
Folgende Begriffe sind für die Farbwahrnehmung grundlegend:
Bei entsprechender Wahl der Farbreize lassen sich Ordinalskalen für die Wahrnehmungsattribute Helligkeit und Farbton bilden (siehe z.B. das Munsell Book of Color. Ledigleich beim Anodnen in bezug auf die Helligkeit können bei den VPn Schwierigkeiten auftreten. Diese Ordinalskalen besitzen auch einen natürlichen Nullpunkt. Eine gleichförmige Farbskala bezeichnet in diesem Kapitel den besonderen Fall von gleichabständigen Intervallskalen, bei dem angrenzenden Intervallen die selbe Zahl zugewiesen wird. Folgende Skalierungsmethoden lassen sich für die Farbwahrnehmung anwenden:
Bei der Verhältnisskalierung erhält man eine Skala mit gleich breiten Intervallen und einem natürlichen Nullpunkt. Folgende Methoden kommen dabei oft zum Einsatz:
Für die Skalierung von Helligkeiten (lightness) läßt sich die Methode der Bisektion anwenden: Dem Beobachter werden ein weißer, ein schwarzer und mehrere graue Chips vorgelegt; er soll einen dieser grauen auswählen, der gleich weit von schwarzen wie vom weißen entfernt ist. Das Intervall zwischen den so gewähltem grauen Chip und den beiden zuvor vorgegebenen Eckpunkten wird wieder auf die selbe Weise unterteilt usw. Auf diese Weise gelangt man zu einer Grauskala.
Farbskalen konstanter Helligkeit (lightness) werden so entwickelt, daß gleiche Abstände der Werte gleichen Schritten in der Farbe entsprechen. Dies ist durch Transformation des Tristimulus-Raums möglich. Empirische Befunde deuten aber darauf hin, daß die Beobachterurteile über Farbunterschiede nicht den für die Konstruktion einer gleichförmigen Skala notwendigen strengen Anforderungen entsprechen. Die Geometrie der Farbwahrnehmung ist also nicht-euklidisch.
Üblicherweise werden die Formeln für dreidimensionale Farbskalen folgendermaßen abgeleitet: Es wird ein Farbigkeits-Diagramm gewählt mit annähernd gleichen Abständen für Farbstimuli gleicher Helligkeit; dazu wird eine Funktion des Luminanz-Faktors hinzugenommen, die zu etwa gleichförmigen Abständen der Helligkeit führt (für Farbreize gleicher Buntheit). Geeignete Skalierungsfaktoren werden sowohl für die Skala der Buntheit als auch für die Skala der Helligkeit so ausgewählt, daß die Einheit der Farbigkeitsunterschiede derjenigen der Helligkeitsunterschiede ähnlich wird.
Folgende drei Prinzipien, die den verschiedenen Farb-Ordnungs-Systemen (color-order systems) zugrunde liegen, lassen sich nennen:
Die Schwelle zur Wahrnehmung von Unterschieden in den Reizen variiert mit der Größe, der Gestalt und der Länge der Reizpulse; dadurch lassen sich die räumlichen und zeitlichen Integrationseigenschaften des visuellen Systems untersuchen.
Grundsätlich lassen sich drei Arten von Theorien zur Farbwahrnehmung untercheiden:
66#66
Dabei sind c (Lichtgeschwindigkeit), h (Plank'sche Konstante) und k (Boltzmann'sche Konstante) Konstanten und T ist die absolute Temperatur in Kelvin.
zurück zu meiner Skriptenseite
zurück zu meiner homepage
Anmerkungen und Mitteilungen an
rainer@zwisler.de