Vortrag im Diplomandenseminar
Lehrstuhl Prof. Drösler
Rainer Zwisler
SS 1997
Nachzulesen in:
In der Wissenschaft allgemein versucht man, beobachtbare Phänomene mit Hilfe mathematischer Modelle zu beschreiben; es sollen also Gesetzmäßigkeiten in Form quantitativer Beziehungen der jeweils zugrundeliegenden Eigenschaften ausgedrückt werden. Dabei wird vorausgesetzt, daß die Ausprägungen der betrachteten Eigenschaften des Forschungsgegenstandes gemessen werden können, also durch Zahlen repräsentiert werden können.
Vor allem in den Sozialwissenschaften werden häufig bilineare Modelle eingesetzt, die den Zusammenhang zwischen Eigenschaften durch Produktsummen erfassen. Diese Zusammenhänge lassen sich durch quantitative Modelle erfassen, bei denen die erhobenen Daten in Form einer Tabelle dargestellt werden: Den zu untersuchenden Objekten (Personen bzw. Gegenständen) werden jeweils Ausprägungen (Werte) verschiedener beobachtbarer Merkmale zugeordnet.
Mit Hilfe von bilinearen Modellen lassen sich Zusammenhänge zwischen Eigenschaften als Summen von Produkten ausdrücken:
wobei es sich bei 
um Variablen handelt, die die untersuchten
Attribute beschreiben. Ein Beispiel ist die Einstellungstheorie von Fishbein &
Ajzen, nach der sich die Einstellung 
einer Person p zu einem Objekt o
Alas Produktsummes aus
, der wahrgenommenen Instrumentalität des Objektes o für den
Wert i bei der Person p und
, der Wichtigkeit des Wertes i bei der Person p 
Orth (1985) hat anhand einiger Beispiele bilineare Modelle aus der Einstellungsforschung betrachtet und analysiert, auf welchem Meßniveau die beteiligten Eigenschaften gemessen werden müssen, um sinnvoll Produktsummen mit den Meßwerten berechnen zu können. Hiernach müssen die jeweiligen Eigenschaften auf Verhältnisskalenniveau gemessen werden. Es muß also mit dem gleichen Informationsgehalt gemessen werden wie in der Längenmessung, was in sozialwissenschaftlichen Zusammenhängen als sehr problematisch gesehen werden muß (meist Rating-Verfahren).
In einem meßtheoretischen Sinne muß man sich an dieser Stelle fragen, unter welchen Voraussetzungen sich ein empirisches Modell eines zu untersuchenden Wirklichkeitsbereichs durch ein derartiges bilineares Modell repräsentieren läßt, d.h. welche Bedingungen ein Datensatz erfüllen muß, damit es überhaupt sinnvoll ist, mit den Meßwerten Produktsummen zu berechnen. Hier soll nun eine meßtheoretische Axiomatisierung diskutiert werden, die eine empirische Überprüfung bilinearer Modelle ermöglicht.
Ziel dieser Arbeit ist es, einen Isomorphismus zu finden zwischen einer
Darstellung der Daten und einer numerischen Beschreibung dieser. Dazu wird
zunächst ein formales Modell des zu untersuchenden Wirklichkeitsbereiches
erstellt, der sogenannte vollständige mehrwertige Kontext 
; dieses formale Modell wird dann durch ein numerisches Modell,
den bilinearen Kontext 
der
Dimension n, repräsentiert. Dann ist das bilineare Modell auch formal
gerechtfertigt, d.h. die damit errechneten Werte sind bedeutsam.
Am Ende der Arbeit steht also ein Repräsentationssatz, der die Bedingungen angibt, unter denen eine Berechnung von Produktsummen (wie sie vom bilinearen Modell vorgenommen wird) im meßtheoretischen Sinne als sinnvoll oder bedeutsam bezeichnet werden kann, also eine Repräsentation durch ein bilineares Modell existiert.
Die Frage der Meßbarkeit der Eigenschaften, die einer empirischen Situation zugrunde liegen, reduziert sich somit auf die Frage nach der Existenz einer Repräsentation durch ein numerisches Modell; diese Frage ist dann rein mathematischer Natur. Diese Fragestellung tritt übrigens vergleichbar in den ``Grundlagen der Geometrie'' als Koordinatisierungsproblem auf.
Zuerst muß nun genau dargelegt werden, was man unter bilinearen Formen zu verstehen hat; insbesondere wird auf den Spezialfall des Skalarproduktes eingegangen.
DEFINITION: Es sei V ein Vektorraum endlicher Dimension auf
einem
Körper K. Eine bilineare Form auf V ist eine Abbildung
für alle 
, welche die Bedingungen
und 
erfüllt.
Man macht die Bedingung (i) deutlich, indem man sagt, daß f linear in der ersten Variable ist und entsprechend die Bedingung (ii), indem man sagt, daß f linear in der zweiten Variable sei. Hierfür zwei Beispiele:
und 
beliebige, lineare Funktionale auf V.
Es
werde furch 
definiert. Dann ist f bilinear, da und beide linear
sind.
, d.h.
wobei 
und 
gelten. Dann ist f eine bilineare
Form auf
.
Eine Bilinearform heißt
symmetrisch, wenn
für alle 
.
Eine symmetrische Bilinearform heißt
positiv definit, wenn
für alle 
mit 
gilt.
DEFINITION: Ist V ein K-Vektorraum, so nennt man eine
positiv
definite symmetrische Bilinearform der Gestalt
ein Skalarprodukt in V.
mit (wobei die Schreibweise 
eben besagt, daß es sich um ein Skalarprodukt handelt)
Wichtig ist, daß man als Ergebnis wieder ein Skalar erhält (daher auch die
Bezeichnung ``Skalarprodukt''). Die dafür charakteristischen Bedingungen
sollen hier noch einmal für den Fall 
zusammengefaßt werden;
für alle 
und 
soll gelten:
,
,
,
,
,
, falls .
Seien 
und 
Spaltenvektoren. Dann ist durch
ein Skalarprodukt in definiert. Dabei ist zu beachten, daß
eine reelle Zahl ist. Die Vektoren u und v werden
orthogonal genannt, wenn ihr Skalarprodukt Null ist.
DEFINITION: Seien K-Vektorräume V und W sowie eine
Abbildung 
gegeben. F heißt K-linear, falls für alle und
gilt:
DEFINITION: Es sei V ein K-Vektorraum. Dann heißt
d.h. der Vektorraum der linearen Abbildungen 
,
der zu
V duale Vektorraum
oder kurz der Dualraum von V. Jedes 
nennt
man
Linearform (oder
lineares Funktional) auf V.
Der Begriff der Basis des Vektorraums V ist definiert als linear unabhängiger aufgespannter Raum, der wiederum aus einer Familie von Vektoren aus V besteht, aus denen sich alle Elemente von V linear kombinieren lassen.
SATZ: Sei V ein endlich-dimensionaler K-Vektorraum und
Dann ist 
eine Basis von
V. Dann gibt es eindeutig bestimmte Linearformen 
mit
eine Basis von 
. Man nennt
die zu 
duale Basis von . Zur Abkürzung verwendet man dabei
oft das Kronecker-Symbol 
.
Jetzt muß also als erstes ein geeignetes Modell zur Beschreibung der Daten gefunden werden. In den meisten Anwendungszusammenhängen sind die erhobenen Daten in Form einer Tabelle gegeben, in der bei den zu untersuchenden Objekten jeweils Ausprägungen verschiedener Merkmale beobachtet werden. Eine Formalisierung dieses häufig auftretenden Datensatztyps findet man in der Formalen Begriffsanalyse, die eine Methode der Datenanalyse entwickelt hat, die auf der mathematischen Ordnungstheorie aufbaut. Der Untersuchungsgegenstand der Formalen Begriffsanalyse sind mehrwertige Kontexte, die folgendermaßen definiert sind:
DEFINITION: Ein mehrwertiger Kontext
Die Elemente der Mengen G, M und W haben folgende Bedeutung:
Gibt es zu jedem 
besteht aus den Mengen G, M und W und einer dreistelligen Relation 
, wobei gilt:
;
;
oder 
.
wird gelesen als ``das Merkmal m hat beim Gegenstand g
den Wert w''; anstelle der Schreibweise kann man auch
schreiben
ein 
mit , so
heißt der Kontext vollständig.
Die Schreibweise m(g) deutet schon an, daß es sich bei m um Funktionen handelt; im bilinearen Kontext sind es dann entsprechend Elemente aus :
Mehrwertige Kontexte sind zur sinnvollen Modellierung von Datensätzen geeignet. Deshalb wird in dieser Arbeit von vollständigen mehrwertigen Kontexten als empirischen Modellen ausgegangen, d.h. es wird angenommen, daß der zu untersuchende Datensatz in Form einer Gegenstand-Merkmal-Tabelle gegeben ist.
Zu diesem empirischen Modell ist nun ein passendes numerisches Modell zu suchen, in dem sich die Produktsummen angemessen modellieren lassen. Das Skalarprodukt ist in der Linearen Algebra der Grundtyp für Produktsummen. Jetzt können wir nun den Begriff des bilinearen Kontextes definieren:
DEFINITION: Sei V ein n-dimensionaler Vektorraum über dem Körper
K und
ein bilinearer Kontext der Dimension n. der Dualraum von V. Dann heißt der mehrwertige Kontext 
, für den die Relation E definiert ist durch
(wobei 
)
Aus dieser Definition läßt sich die zentrale Frage dieser Arbeit formulieren:
Zur Beantwortung dieser Frage muß eine Addition und eine Multiplikation auf W so definiert werden, daß W mit diesen Operationen einen Körper bildet (man muß mit den Elementen aus W, also den Testergebnissen, rechnen können) und es müssen die Bijektionen
mit 
und
mit 
gefunden werden, so daß gilt:
Im folgenden wird ein Repräsentationssatz angegeben, der die Bedingungen für die
Existenz einer Addition, Multiplikation und Bijektion darlegt, so daß
sichergestellt ist, daß das Paar 
einen Isomorphismus zwischen
den mehrwertigen Kontexten (G, M, W, I) und 
herstellt. Dann läßt sich der Wert w = m(g) eines
Attributes folgendermaßen bestimmen:
wobei dem Objekt g der Vektor 
entspricht und dem
Merkmal m der durch die Linearform beschriebene Vektor 
; außerdem muß gelten 
.
Bei der Untersuchung mehrwertiger Kontexte führt man diese häufig auf einwertige Kontexte zurück, indem man die Merkmalsausprägungen durch einwertige Merkmale interpretiert.
DEFINITION: Unter einwertigen Kontexten versteht man Kontexte, bei denen die Wertemenge W nur ein einziges Element besitzt.
Betrachtet man einen mehrwertigen Kontext (G, M, W, I), so erhält man zu jeden
Wert r aus W einen einwertigen Kontext 
, bei dem 
folgendermaßen definiert ist:
Dann lassen sich definieren:
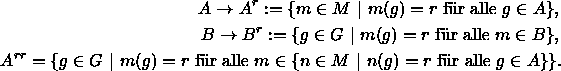
In Worten läßt sich dies so ausdrücken:
entspricht der Menge an Merkmalen 
, die bei allen
Gegenständen den Wert r annehmen. Die Abbildung ordnet also den Gegenständen
g aus den Teilmenge 
Merkmale m aus der gesamten
Merkmalsmenge M zu.
entspricht der Menge an Gegenständen 
, die bei allen
Merkmalen den Wert r annehmen. Die Abbildung ordnet also den Merkmalen m
aus den Teilmenge 
Gegenstände g aus der gesamten
Gegenstandsmenge G zu.
ist schließlich folgendermaßen zu verstehen: Für eine bestimmte
Menge an Gegenständen nimmt man diejenige Menge an Merkmalen
, die bei allen Gegenständen den Wert r annehmen. Zu diesen
Merkmalen sucht man dann diejenigen Gegenstände 
, die bei
allen Merkmalen 
den Wert r annehmen.
Der folgende Satz besagt nun, daß für einen festen Wert r die durch die
Hüllenoperatoren 
und 
definierten Hüllensysteme
mit 
vollständige Verbände sind, zwischen denen die
Ableitungsoperatoren und inverse Antiisomorphiosmen induzieren:
SATZ: Für den Kontext
und
Dann sind
definiert durch
bilden dann für jedes gelte
und 
vollständige Verbände mit dem Supremum
und
dem Infimum 
, wobei 
bzw. 
für alle 
. Die Abbildungen
zueinander inverse Antiisomorphismen zwischen
und 
. Deshalb schreibt man oft
anstelle von 
auch 
.
Bemerkenswert ist hier, daß in dem bilinearen Kontext für 
offensichtlich immer gilt:
Im allgemeinen besitzen mehrwertige Kontexte diese Eigenschaft nicht; dies
bedeutet, daß diese Eigenschaft, wenn sie nicht aus den anderen geforderten
Bedingungen folgt, für einen mehrwertigen Kontext postuliert werden muß,
wenn man ihn durch einen bilinearen Kontext repräsentieren will. Für den
mehrwertigen Kontext und 
benötigt man
dazu die beiden Bedingungen 
bzw. 
, die
folgendermaßen festgelegt werden:
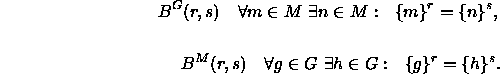
Zur Verdeutlichung: 
hat folgende Bedeutung: die Menge aller
Gegenstände, die beim Merkmal m den Wert r haben.
In Worten lassen sich diese Bedingungen folgendermaßen ausdrücken:
fordert, daß für alle Merkmale auch Merkmale 
existieren, für die gilt 
, d.h. die Menge an Gegenständen
, die bei dem Merkmal m den Wert r annehmen, soll gleich der Menge
an Gegenständen , die bei dem Merkmal n den Wert s annehmen, sein.
Anders formuliert: Für
alle Merkmale m existieren Merkmale n, so daß gilt, daß die Menge aller
Gegenstände, die bei dem
Merkmal m den Wert r haben gleich der Menge aller Gegenstände, die bei dem
Merkmal n den Wert
s haben, ist fordert, daß für alle Gegenstände auch Gegenstände
existieren, für die gilt 
, d.h. die Menge an
Merkmalen , die bei dem Gegenstand g den Wert r annehmen soll
gleich der Menge an Merkmalen , die bei dem Gegenstand h den Wert
s annehmen, sein.
Dazu läßt sich der folgende Hilfssatz aufstellen:
HILFSSATZ: Sei
Gilt ein mehrwertiger Kontext und
. In 
gilt genau dann 
, wenn den Bedingungen und 
genügt, und es gilt 
, wenn
den Bedingungen und 
genügt.
bzw. , so ist 
bzw. 
ein Automorphismus von 
bzw. 
.
Diese Idee soll nun auf mehrwertige Kontexte übertragen werden. Empirisch sieht
dies bei einem in Form eines mehrwertigen Kontextes gegebenen Datensatz so aus:
Es ist sinnvoll, zu jedem Merkmal alle Gegenstände, die für dieses Merkmal die
selbe Ausprägung haben, zusammenzufassen und dabei alle Ausprägungen zu
durchlaufen. Deshalb definiert man zu jedem Merkmal m des mehrwertigen
Kontextes (G, M, W, I) eine Äquivalenzrelation 
auf G
durch
und entsprechend zu jedem Gegenstand eine Äquivalenzrelation
auf M durch
Somit sind
und
Mengenzuerlegungen in Äquivalenzklassen mit gleichem Wert r
für und ; außerdem ist
die Menge aller Gegenstände aus G, die beim Merkmal m alle den selben Wert m(g) haben, und
die Menge aller Merkmale aus M, die beim Gegenstand g alle den selben Wert
m(g)
haben, wobei 
die Äquivalenzklasse von ist, die g
enthält, und 
die Äquivalenzklasse von ist, die m
enthält. Auf diese Weise läßt sich also eine Zerlegung von G bzw. von M in
Äquivalenzklassen mit
gleichem Wert m(g) erzeugen.
Der Begriff Rahmen stammt von John von Neumann und kann als verbandstheoretisches Gegenstück der Koordinatensysteme in der projektiven Geometrie verstanden werden. Im folgenden wird nun jeweils ein Rahmen in den Äquivalenzrelationenverband von G und M eingeführt.
Jeder Vektorraum V hängt mit seinem Dualraum strukturell eng zusammen:
Zu jeder Basis von V existiert eine eindeutig bestimmbare Dualbasis von
. Deshalb sollen nun die Rahmen in den Äquivalenzrelationenverbänden von
G und M auf ähnliche Weise zusammenhängen. Dies kommt in der Definition des
Doppelrahmens zum Ausdruck. Zuerst werden jedoch die folgenden
Schreibweisen eingeführt:
Sind 
fest gewählte Elemente aus G und 
fest gewählte Elemente aus M, so schreibt man für 
mit 
Dies bedeutet folgendes:
bezeichnet also diejenige Äquivalenzrelation zwischen zwei
Elementen aus G, die zutrifft, wenn der Wert der beiden Objekte bezüglich des
Merkmals 
gleich ist; es handelt sich also um alle Elemente aus G, die
beim
Merkmal den selben Wert haben:
diejenige Äquivalenzrelation zwischen
zwei Elementen aus M, die zutrifft, wenn der Wert der beiden Merkmale am
Objekt 
gleich ist; es handelt sich also um alle Elemente aus M, die beim
Gegenstand den selben Wert haben:
Außerdem wird folgende Schreibweise eingeführt:
In Worten läßt sich dies so formulieren:
bezeichnet diejenige Äquivalenzrelation zwischen zwei
Elementen aus G, die zutrifft, wenn der Wert der beiden Objekte bezüglich
aller von den Merkmalen und 
verschiedenen Merkmale gleich ist;
es handelt sich also um die Menge aller Elemente aus G, die bei allen
Merkmalen
außer und den selben Wert haben.
bezeichnet diejenige Äquivalenzrelation zwischen zwei
Elementen aus M, die zutrifft, wenn der Wert der beiden Merkmale bei allen
Objekten, die von und 
verschieden sind, gleich ist; es handelt sich
also um die
Menge aller Elemente aus M, die bei allen Gegenständen außer und
den
selben Wert haben.
Für die den Gegenstand g enthaltende Äquivalenzklasse 
von
schreibt man kurz 
, und für die Äquivalenzklasse
von wird 
geschrieben.
bezeichnet also die Äquivalenzklasse, die alle Gegenstände enthält, die bei
allen Merkmalen
außer und den selben Wert 
haben.
Für werden die entsprechenden Bezeichnungen benutzt:
ZUR ERINNERUNG: Eine Abbildung ist surjektiv, gdw. sie rechtstotal ist (jedem Element des Wertebereichs wird eines aus dem Definitionsbereich zugeordnet).
DEFINITION: Sei (G, M, W, I) ein mehrwertiger Kontext. Dann heißt
ein geordnetes 2(n+1)-tupel
ein Doppelrahmen der Ordnung n in (G, M, W, I), wenn es zwei Elemente
0, 1 in W gibt mit 
(wobei 
) für
alle 
und wenn für alle mit die
folgenden
Bedingungen gelten:
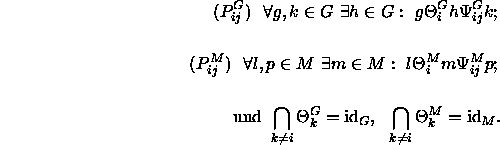
bezeichnet alle Gegenstände, die bei allen
Merkmalen außer den selben Wert haben. Die Bedingung 
besagt also,
daß jeweils zwei Objekte bei mindestens einem Attribut unterschiedliche Werte
haben (sonst kann man sie als ein und das selbe Objekt betrachten). Für die Merkmale
gilt das selbe. Diese Forderung läuft darauf hinaus, daß (G, M, W, I) keine
zwei gleichen Zeilen oder Spalten besitzt. Diese Bedingung stellt keine starke
Forderung dar, da man einfach gleiche Zeilen oder Spalten miteinander
identifizieren kann. Die Bedingungen 
und
garantieren insbesondere auch die Existenz von 
und 
.
Dann ist für 
die Bedingung 
äquivalent zu der Eigenschaft, daß jedes Merkmal von
M funktional abhängig ist von 
.
Außerdem stellt die Bedingung 
sicher, daß
nicht funktional abhängig ist von 
für alle . Deshalb bilden die Einheitsattribute eine
``Basis'' bezüglich der funktionalen Abhängigkeit in M; für die Objekte gilt
dies ähnlich.
Ein Doppelrahmen heißt surjektiv, falls
für alle 
.
Sei K ein Körper. Dann ist
ein surjektiver Doppelrahmen des bilinearen Kontextes 
,
wobei
die kanonische Basis von 
ist,
ihre Dualbasis ist,
und
.
Ziel ist es nun, für jeden vollständigen mehrwertigen Kontext (G, M, W, I),
der einen surjektiven Doppelrahmen der Ordnung n besitzt, ``kanonische''
Bijektionen 
und 
von G und M auf 
anzugeben. Dazu sind
zunächst einige Aussagen über die durch einen Doppelrahmen gegebenen
Äquivalenzrelationen 
(beziehungsweise 
) erforderlich.
Ebenso wie in der projektiven Geometrie mit Hilfe von Koordinatensystemen kann
man mit Hilfe der Rahmen 
und 
Bijektionen von G und M auf definieren.
SATZ: Sei (G, M, W, I) ein vollständiger mehrwertiger Kontext.
Existiert in (G, M, W, I) ein surjektiver Doppelrahmen
Bijektionen von G bzw. M auf 
, so sind die Abbildungen 
und 
mit
.
Im folgenden werden die zwei weitere Abkürzungen eingeführt:
ist die Kurzform für 
; es bezeichnet
also denjenigen Gegenstand g, der bei allen Merkmalen 
den
Wert 
hat. ist die Kurzform für 
; es bezeichnet
also dasjenige Merkmal m, das bei allen Gegenständen 
den
Wert 
hat.
einfach nur
geschrieben. (Zur Erinnerung: 
, also die
Menge aller Gegenstände, die beim Merkmal m den Wert r haben.
REPRäSENTATIONSSATZ: Sei n eine natürliche Zahl größer als 2. Ein
vollständiger mehrwertiger Kontext (G, M, W, I) mit ausgezeichneten
Elementen
ist genau dann isomorph zu einem bilinearen Kontext
der Dimension n, wenn (G, M, W, I) für alle 
den
Bedingungen und genügt und bezüglich 0, 1 einen
surjektiven Doppelrahmen 
der Ordnung n besitzt, so daß die folgenden fünf Axiome gelten:
und 
gilt 
und 
.
und 
für alle
mit 
und
, dann existiert ein Merkmal m ungleich mit m(g) = m(h);
dabei kann 
gewählt werden, wenn 
gilt.
für ein und 
für alle 
, dann gilt für jedes :
und 
mit 
existiert stets ein mit 
und zu jedem
Merkmal 
existiert ein Wert mit 
bzw. 
.
Gilt dieser Repräsentationssatz, dann existiert ein bilinearer Kontext ,
den Bedingungen und
genügt;
ist ein
surjektiver Doppelrahmen der Dimension n in .
Wille(1994) zeigt, daß in mit dem Doppelrahmen 
zusätzlich die Axiome (A0) - (A4) gelten.
Der Repräsentationssatz gibt also die Bedingungen an, unter denen ein
vollständiger mehrwertiger Kontext (G, M, W, I) isomorph zu einem bilinearen
Kontext der Dimension n > 2 ist. Ist dies der Fall,
dann läßt sich ein Attributwert m(g) folgendermaßen berechnen:
wobei das Objekt g dem Vektor entspricht und das
Attribut m entspricht der Linearform, die durch den Vektor 
beschrieben wird.
Hier zeigt sich, daß die Annahme der bilinearen Repräsentation eines
vollständigen mehrwertigen Kontextes damit zusammenhängt, daß jeder Wert m(g)
als Komposition der Werte von g bezüglich m in verschiedenen ``Zuständen''
abhängt. Um dies zu betonen, bezeichnet man den Wert m(g) als einen
zusammengesetzten Wert (aggregate value), der sich aus bestimmten
Zustandswerten (state values) 
von g bezüglich m im Zustand
i zusammensetzt.
Die natürliche Zahl n läßt sich als die Anzahl der betrachteten Zustände interpretieren; die Menge der Zustäde werde bezeichnet durch
Zusammenfassend kann man also sagen, daß im Falle eines Isomorphismus von (G, M, W, I) auf ein zusammengesetzter
Wert m(g) sich aus den Zustandswerten 
zusammensetzt,
wobei
und
.
Dabei ist zu beachten, daß hier nicht einfach Objekte und Merkmale betrachtet werden, sondern Objekte und Merkmale in bestimmten Zuständen, die durch eine gegebene Zustandsmenge Z festgelegt sind.
Zur Wiederholung der Repräsentationssatz:
Sei n eine natürliche Zahl größer als 2. Ein
vollständiger mehrwertiger Kontext (G, M, W, I) mit ausgezeichneten
Elementen ist genau dann isomorph zu einem bilinearen Kontext
der Dimension n, wenn (G, M, W, I) für alle den
Bedingungen und genügt und bezüglich 0, 1 einen
surjektiven Doppelrahmen
der Ordnung n besitzt, so daß die fünf Axiome (A0) – (A4) gelten.
Die erste Voraussetzung für den Repräsentationssatz ist, daß für (G, M, W, I)
für alle Werte die Begingungen und
erfüllt sind. Zur Wiederholung:
bedeutet: Für alle Merkmale m existieren Merkmale n, so daß
gilt, daß die Menge an Gegenständen , die bei dem Merkmal m den Wert
r annehmen, gleich sein soll der Menge an Gegenständen sein, die bei dem
Merkmal n den Wert s annehmen.
Die zweite Annahme des Repräsentationssatzes ist die Existenz eines surjektiven
Doppelrahmens 
unter bezug
auf festgelegte Elemente 0 und 1 aus W. Der Wert 0 läßt sich als
Gleichgewichtswert (equilibrium value) interpretieren; der Wert 1 kann
als Einheit (unit value) für die auf der Grundlage des
Doppelrahmens erarbeitete Koordinatisierung verstanden werden.
Der Doppelrahmen führt auf natürliche Weise zu Bijektionen
und 
, die
folgendermaßen definiert sind:
Die Bedingung für einen Doppelrahmen,
legt es nahe, die Objekte von als
Einheitsobjekte zu bezeichnen und die Attribute von als Einheitsattribute. Das restliche Objekt 
und das restliche
Attribut 
spielen eine verbindende und vereinende Rolle für die
Dimensionen, die von und von begründet
werden. Deshalb bezeichnet man als das vereinheitlichende Objekt und
als das vereinheitlichende Merkmal des Doppelrahmens .
(A0) Für und gilt und .
Zuerst zur Klärung der Bestandteile des Axioms (A0):
: Zu allen Gegenständen , die bei dem Merkmal m
die Ausprägung 0 haben, wird die Menge an Merkmalen gesucht, bei denen diese
Gegenstände den Wert 1 haben. Dazu wiederum sucht man die Menge an Gegenständen,
bei denen diese Merkmale die Ausprägung r besitzen.
Alle Merkmale, die bei den Gegenständen, die bei Merkmal m den Wert 0 haben, den Wert 1 haben; dazu die Gegenstände, die bei dieser Merkmalsmenge den Wert r haben.
: Alle Gegenstände , die
bei dem Merkmal m die Ausprägung 0 haben (also g(m) = 0). : ist die Kurzform für ; wobei die
Bijektion
bezeichnet also denjenigen Gegenstand g, der bei allen Merkmalen den Wert hat.
Es wird also gefordert, daß
für alle und
für alle .
wird auch das Gleichgewichtsattribut (equilibrium attribute)
genannt und wird auch als das Gleichgewichtsobjekt (equilibrium
object) bezeichnet.
(A1) Ist und für alle
mit und
, dann existiert ein Merkmal m ungleich mit m(g) = m(h);
dabei kann gewählt werden, wenn gilt.
Nach diesem Axiom existiert ein
Merkmal m ungleich , für das m(g) = m(h) gilt. Auch
hierbei handelt es sich um ein ``Reichhaltigkeits''-Bedingung (richness
condition).
Zur Erinnerung: Bei der Definition des surjektiven Doppelrahmens wurde festgelegt:
Also 
.
Interessanter ist der zweite Teil von (A1), der fordert, daß für alle 
und gelten soll
Eine besondere Folge davon ist, daß 
für alle ; dies bedeutet, daß 
für ein
Element 
. Somit sichert (A1) den vereinigenden Charakter von .
(A2) Ist für ein und für alle , dann gilt für jedes :
Unter Zuhilfenahme von Axiom (A1) läßt sich 
folgendermaßen formulieren:
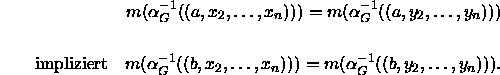
Dies soll zeigen, daß das Axiom (A2) eine ähnliche Rolle spielt wie das Axiom P2 im Savage's Expected-Utility-Theorem von Fishburn (1970), das sich folgendermaßen interpretieren läßt: ``P2 besagt, daß die Handlungspräferenzen nicht von denjenigen Zuständen abhängen sollen, die bei den beiden Handlungsalternativen zu den selben Konsequenzen führen.'' Eine ähnliche Interpretation für das Axiom (A2) läßt sich so formulieren:
(A2) besagt, daß die Gleichheit von zusammengesetzten Werten (aggregate values) von Objekten bezüglich eines festen Attributs m nicht von denjenigen Zuständen abhängen soll, die identische Zustandswerte bei den beiden Objekten bezüglich m besitzen.
Interpretiert man das Paar (A, B) mit 
und 
als einen
``natürlichen'' Begriff (concept) von mit der
Extension A und der Intension B, dann drückt dieser Antiisomorphismus in
mathematischen Begrifen aus, was in der Philosophie bekannt ist als das
Gesetz der Reziprozität für Begriffe (reciprocity law for concepts).
Nach dieser Interpretation führen die Bedingungen
und zu einer Übereinstimmung zwischen den
extensionalen Strukturen:
und von intensionalen Strukturen:
(Zur Erinnerung: 
und gdw. und
gelten).
(A3) Zu und mit existiert stets ein mit .
Anstelle von 
Man kann man die Bestandteile des Axiom (A3) auch ausführlicher schreiben:
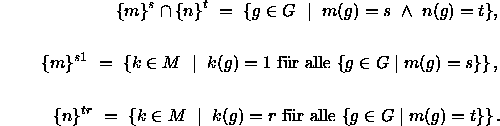
Auf ähnliche Weise wie bei (A0) läßt sich zeigen, daß (A3) in gilt: Seien 
und 
zwei verschiedene zueinander
parallele Hyperebenen in , die 
nicht enthalten. Dann gibt es, wie
wir aus der analytischen Geometrie wissen, eine Streckung, die auf
abbildet; d.h. es gibt ein 
mit
. Damit folgt, daß zu und
ein r existiert mit 
.
Axiom (A3) besagt, daß die extensionale Struktur 
stark
symmetrisch ist; dies gilt auch für die intensionale Struktur 
: Für alle ist die Verkettung ein Automorphismus auf
Das Axiom (A3) fordert dann, daß jedes beliebige Coatom 
von
abgebildet werden kann auf jedes unverbundene Coatom
mit Hilfe eines speziellen Automorphismus 
( 
ist wie folgt definiert: 
). Dieser Automorphismus läßt sich geometrisch verstehen als die
Streckung um den Faktor r, der durch das Gleichgewichtsobjekt
festgelegt ist.
(A4) Zu jedem Gegenstand und zu jedem
Merkmal existiert ein Wert mit bzw. .
Unter der Annahme der Bedingungen und fordert das Axiom
(A4), daß
die Menge der Atome
und
die Menge der
Coatome
für alle ist. Dementsprechend soll gelten, daß
die Menge der Atome
und
die Menge der
Coatome
für alle ist. Somit handelt es sich bei (A4) um eine weitere
Reichhaltigkeitsbedingung, da sie fordert, daß Objekte durch Merkmale
unterschieden werden können und daß Merkmale durch Objekte getrennt werden
können.
Die Mengen bzw. 
mit 
werden als Gegenstands- bzw. Merkmalshyperebenen
bezeichnet.
Das Repräsentationstheorem setzt einen allgemeinen Rahmen für die Analyse bilinearer Modelle. Möglicherweise existieren Datenkontexte, bei denen sich die Voraussetzungen für das Repräsentationstheorem nachweisen lassen; dann wäre ein bilinearer Kontext eine geeignete Beschreibung der Daten.
In den meisten Fällen sind die Daten jedoch mehr oder weniger unvollständig. Dann stellt sich die Frage, ob sich die vorgegebenen Daten durch potentielle Objekte, Attribute und Werte so erweitern lassen, daß sie einen vollständigen mehrwertigen Kontext bilden, der zu einem bilinearen Kontext isomorph ist. Für die Anwendung der bilinearen Modelle sollte sich die Forschung deshalb auf das folgende Problem konzentrieren:
Unter welchen Annahmen kann ein vollständiger mehrwertiger Kontext so in einen bilinearen Kontext eingebettet werden, daß die extensionalen und
die intensionalen Strukturen von berücksichtigt werden?
Nach: Orth, B. (1985). Bedeutsamkeitsanalysen bilinearer Einstellungsmodelle. Zeitschrift für Sozialpsychologie, 16, S. 101-115.
In dieser Arbeit geht es darum, wann Aussagen aufgrund von Skalenwerten empirisch bedeutsam sind; um Bedeutsam zu sein, muß eine numerische Aussage auch für alle gleichwertigen Skalen gelten. Diese Forderung läuft darauf hinaus, daß eine Aussage aufgrund von Skalenwerten gleichermaßen für die zulässig transformierten Skalenwerte der beteiligten Skalen gelten muß. Gleichwertige Skalen liegen somit dann vor, wenn sie jeweils durch zulässige Transformationen ineinander überführbar sind. Dabei spielen die verschiedenen Skalentypen eine wichtige Rolle bei der Untersuchung der Bedeutsamkeit numerischer Aussagen.
DEFINITION: Eine numerische Aussage ist sinnvoll ( bedeutsam) dann und nur dann, wenn sich ihr Wahrheitswert (``wahr'' oder ``falsch'') unter allen zulässigen Transformationen der betreffenden Skala (oder Skalen) nicht ändert.
Anzumerken ist, daß sich der Begriff der Bedeutsamkeit immer auf Aussagen bezieht und nicht auf Rechenoperationen oder z.B. statistische Methoden der Datenauswertung: Nicht die Rechenoperationen oder statistischen Tests sind sinnvoll, sondern die Aussagen, die mit Hilfe dieser Operationen oder Tests aufgrund von Meßwerten gemacht werden. (z.B. statistische Hypothesen, die getestet werden sollen).
Die zulässigen Transformationen charakterisieren den Zusammenhang zwischen gleichwertigen Skalen, also zwischen Skalen, die gleichermaßen homomorphe Abbildungen eines empirischen Relativs in das selbe numerische Relativ sind. Hier seien nun einige häufig vorkommende Klassen zulässiger Transformationen von Skalen beschrieben, die die verschiedenen Skalentypen oder Skalenniveaus bestimmen.
Es wurde gezeigt, daß bilineare Modelle der Form
oder (wenn F eine monoton steigende Funktion ist und A, B, C Variablen sind)
keine sinnvollen numerischen Aussagen sind, sofern die Variablen A und B auf Ordinal- oder Intervallskalenniveau gemessen sind (unabhängig vom Niveau der Skala C). Dagegen müssen die Skalen A, B mindestens Verhältnisskalenniveau besitzen, also
damit die oben genannten Aussagen (das bilineare Modell) sinnvoll bzw. bedeutsam sind.
Es läßt sich zeigen, daß die Annahmen in Form der Gleichungen 
bzw. 
derart modifiziert werden können, daß sie sinnvolle numerische Aussagen sind,
wenn die Variablen A und/oder B lediglich Intervallskalenniveau haben. Dazu
betrachtet man anstelle von Gleichung die
folgende Gleichung
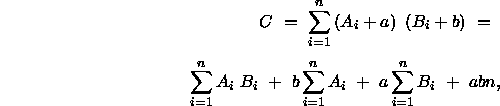
wobei a und b reelle Konstanten sind. In dieser Arbeit wird gezeigt, daß ein Modell nach dieser Gleichung, das ebenfalls ein bilineares Modell ist, lediglich Intervallskalenniveau für alle Variablen erfordert.
Für den Fall, daß A Verhältnis- oder Absolutskala und B Intervallskala ist, kann anstelle der letzten Gleichuung die folgende Modellgleichung betrachtet werden,
wobei b eine reelle Konstante ist. Diese Gleichung könnte beispielsweise dann in Betracht kommen, wenn die Variable A als subjektive Wahrscheinlichkeit nicht nur interpretiert, sondern auch gemessen wird und dann eine Absolutskala ist. Sinnvoll sind Vergleiche von Einstellungswerten aufgrund eines bilinearen Ausdrucks in dieser letzten Gleichung jedoch auch, wenn A nur Verhältnisskala und B Intervallskala ist.
Nach: Falmagne, J.C. (1972). Biscalability of Error Matrices and All-or-None Reaction Time Theories. Journal of Mathematical Psychology, 9, pp 206-224.
Falmagne betrachtet einen Spezialfall des bilinearen Modells, das multiplikative biskalierbare Modell, dem folgende Grundgleichung zugrunde liegt:
Werden bei dieser multiplikativen Verknüpfung anstelle von Skalaren a und x Vektoren eingesetzt, müßte man das Skalarprodukt verwenden. Es würde sich somit um einen bilineares Modell handeln.
Das hier präsentierte Modell wurde für ein experimentelles Paradigma konstruiert, bei dem eine Reaktion von mehreren möglichen Alternativen ausgeführt werden soll (choice reaction situation); der Versuchsperson ist bereits vor dem Durchgang bekannt, welches die richtige Reaktion für jeden Reiz ist. Auch nach intensivem Training können dabei noch Fehler auftreten, die die Reize und die Reaktionen nicht mit perfekter Genauigkeit unterschieden werden können, wegen des Zeitdrucks, Vergessens usw.
Als Daten erhält man die bedingten relativen Häufigkeiten für die verschiedenen Reaktionsklassen, wobei die einzelnen Reize gegeben sind. Solche Daten werden üblicherweise als Konfusionsmatrix bezeichnet.
Nun müssen zuerst die Bestandteile unserer Theorie definiert werden:
bezeichnet.
bezeichnet.
sei eine Abbildung 
, die bestimmten
Reizen bestimmte Reaktionen zuordnet. 
bezeichnet die für den Reiz
x korrekte Reaktion.
, die die
Randbedingung 
für alle 
erfüllt. Unter
diesen Voraussetzungen kann P(a, x) als die bedingte Wahrscheinlichkeit
für die Reaktion a gegeben Reiz x interpretiert werden.
DEFINITION: Treffen die gerade genannten Bedingung zu, dann kann
man 
als eine (positive) Konfusionsmatrix bezeichnen.
Die Menge der Wahrscheinlichkeiten in einer Konfusionsmatrix kann durch einen Reizfaktor v(x) und durch einen Reaktionsfaktor u(a) (z.B. eine Tendenz zu bestimmten Reaktionen) erklärt werden. Es lassen sich zwei abstrakte Formen dieser Überlegung betrachten, ein allgemeines biskalierbares und ein spezielle multiplikatives biskalierbares Modell:
Es seien u und v reellwertige Funktionen auf R bzw. S; es gilt also
und 
. Dann sei 
die Menge aller Reiz-Reaktionspaare (a, x), für die
gilt 
(es handelt sich also um alle Reiz-Reaktionspaare,
die ``falsch'' sind). 
sei das Komplement von P bezüglich
K, also die Menge der ``richtigen'' Reiz-Reaktionspaare.
Die Funktion F sei eine reellwertige Funktion, die auf allen Paaren von
Zahlen der Form (u(a), v(x)) definiert ist, wobei 
gelten muß.
Nun werde angenommen, daß
für alle . Erfüllt eine Konfusionsmatrix diese Bedingungen, wird
sie als biskalierbar bezeichnet. Hierbei handelt es sich um einen
Spezialfall der verbundenen Messung; dies zeigt sich in der
Tatsache, daß eine partielle Ordnung auf dem kartesischen
Produkt 
induziert.
In manchen Fällen des bilinearen Modells ist der folgende Spezialfall einer biskalierbaren Konfusionsmatrix von Interesse: Es seien u und v wie oben definiert, wobei u > 0 und v > 0 gelten soll. Es werde angenommen, daß
für alle . Eine Konfusionsmatrix, die dieser Bedingung genügt,
wird als eine multiplikative Konfusionsmatrix bezeichnet.
Diese Bedingung kann als eine Verallgemeinerung der Bedingung der Quasi- Unabhängigkeit betrachtet werden.
Es existiert ein Verbindungsglied zwischen der Biskalierbarkeit und der Multiplikativität; dabei handelt es sich um die folgende Repräsentation (die hier nicht näher behandelt wird):
Es sei eine Konfusionsmatrix. Es läßt sich zeigen,
daß wenn R nur zwei Elemente enthält die Konfusionsmatrix immer
multiplikativ ist. Deshalb wird im folgenden davon ausgegangen, daß R
mindestens drei Elemente enthält.
In diesem Fall werden angenommen, daß
, genügen;
;
.
Daher gilt wenn 
, dann
Das selbe Argument ergibt sich, wenn F im ersten Argument fallend ist. Aus Symmetriegründen ergeben sich hieraus die Bedingungen:
):
und
, dann ist 
.
):
und
, dann ist 
.
):
und
, dann ist 
Enthält die Reizmenge R mehr als drei Elemente, dann sind die Bedingungen
(BS ) und (BS )
äquivalent zu den folgenden:
'):
, dann ist
.
'):
, dann ist
.
Die bisher dargestellten Ergebnisse münden im Theorem 1:
THEOREM 1: Es sei 
eine
Konfusionsmatrix, in der R mindestens drei Elemente enthält. Dann ist
biskalierbar, genau dann, wenn sie den Bedingungen
(BS ) - (BS ) genügt. Außerdem sind diese Bedingungen
unabhängig.
Nun wird wieder angenommen, daß R mindestens drei Elemente enthält; man betrachte die Folgende Bedingung (M), die notwendig und hinreichend dafür ist, daß eine Konfusionsmatrix multiplikativ ist:
für alle 
.
THEOREM 2: Es sei eine
Konfusionsmatrix, in der R mindestens drei Elemente enthält. Dann ist
multiplikativ, genau dann wenn die Bedingung (M)
gilt.
Es ist zu beachten, daß die Bedingung (M) die Bedingung (M') impliziert:
für alle 
. Wichtig ist dabei, daß im
allgemeinen die Bedingung (M') nicht die Bedingung (M) impliziert. Wenn R
allerdings mindestens vier Reaktionen enthält, dann sind (M) und (M')
äquivalent.
Das nächste Theorem löst die Eindeutigkeitsfrage:
THEOREM 3: Es sei eine
Konfusionsmatrix, in der R mindestens drei Elemente enthält. Wenn (u, v),
(u', v') zwei Paare von streng positiven Funktionen sind, die die Bedingung
(2), also 
, für alle erfüllen,
dann existiert eine Konstante C > 0, so daß für alle 
gilt:
Nach der Grundgleichung des allgemeinen Modells, , handelt es sich bei F um eine beliebige, in ihren beiden
Argumenten streng monotone Funktion; dabei ist nur die von auf
dem kartesischen Produkt induzierte Ordnung für die Theorie
relevant. Eine biskalierbare Konfusionsmatrix ist deshalb ein Spezialfall
der verbundenen Messung (conjoint measurement).
Die Axiome (BS ') und (BS ')
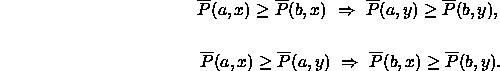
sind entweder direkt Teil aller Theorien zur verbundenen Messung oder aus
ihnen ableitbar. Es handelt sich dabei um Unabhängigkeitsaxiome, die
sicherstellen, daß die Relation 
getrente Ordnungen auf R und S
ermöglicht.
Es zeigt sich aber der folgende Unterschied zwischen Theorien zur
Biskalierbarkeit und zur verbundenen Messung: induziert nur
eine partielle Ordnung auf anstelle einer totalen Ordnung.
Hieraus ergibt sich die Konsequenz, daß (BS )
nicht direkt aus den beiden Bedingungen (BS ) und (BS )
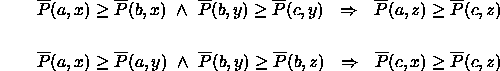
abgeleitet werden kann; bei (BS ) handelt es sich um ein neues Axiom.
Nach: Wandmacher, J. (1977). S-Multiplicativity of a Stochastic Matrix and Applications to Visual Identification. Journal of Mathematical Psychology, 16, pp. 219-233.
Wandmacher verallgemeinert das Konzept der multiplikativen Konfusionsmatrizen
von Falmagne zu dem Konzept der S-Multiplikativität. Dabei geht
Wandmacher von einer Teilmenge 
aus. In dem Modell von Falmagne (I1972) würde S
genau alle falschen Reiz-Reaktions-Paare enthalten; es geht also um alle
Elemente außerhalb der Hauptdiagonalen; Wandmacher nennt sie deshalb auch
-Multiplikativität.
Im folgenden sei 
eine stochastische Matrix; 
läßt
sich dann als die bedingte Wahrscheinlichkeit für die Reaktion mit dem
Index j unter der Bedingung des Reizes mit dem Index i interpretieren.
Falmagne würde dafür schreiben P(a, x).
Ein einfaches Modell für derartige stochastische Matrizen besteht darin,
die bedingten Wahrscheinlichkeiten als Produkt zweier Funktionen zu
analysieren, von denen eine vom Reiz und die andere von der Reaktion
abhängt. Diese Dekomposition muß nicht unbedingt für die gesamte Matrix
(indexiert durch Elemente aus I) gelten, sondern kann auch nur bei einem
Teil (indexiert durch Elemente aus 
) davon zutreffen.
Präziser wird dies in der Definition 1 dargestellt:
DEFINITION 1: Sei
Dabei schreibt man zur Vereinfachung iSj, um auszudrücken, daß 
eine Menge von Indizes; weiterhin sei 
eine stochastische Matrix ( 
). Man nennt dann P S-multiplikativ, genau dann wenn und zwei reellwertige Funktionen u und v existieren, so
daß gilt
.
Falmagne (1972) zeigt einige Verbindungen zwischen der D-Multiplikativität
als formales Merkmal einer stochastischen Quadratmatrix und verschiedenen
Prozessmodellen für die perzeptuelle Identifizierung und für das
Wahlverhalten; diese Modelle sagen -multiplikative
Konfusionsmatrizen vorher. Von besonderem Interesse ist hierbei das Alles-
oder-Nichts-Modell von Townsend (1971). Demnach wird der dargebotene Reiz
i entweder mit der Wahrscheinlichkeit 
identifiziert oder es ist
keine Information über den präsentierten Reiz verfügbar und die
Versuchsperson rät eine Reaktion j mit der Wahrscheinlichkeit 
. Das
Alles-oder-Nichts-Modell sagt deshalb eine Konfusionsmatrix nach der
folgenden Gleichung vorher (wobei die Reaktion i die einzige für den Reiz
i richtige Reaktion sein soll):
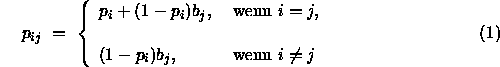
und 
. Gleichung (1) impliziert D-
Multiplikativität; später wird sich allerdings zeigen, daß bei Experimenten
zur perzeptuellen Identifizierung die empirisch gewonnenen
Konfusionsmatrizen nicht D-multiplikativ sein müssen und somit das Alles-
oder-Nichts-Modell kein allgemein geeignetes Modell der perzeptuellen
Identifizierung darstellt: In der vorliegenden Studie werden
Konfusionsmatrizen auf D-Multiplikativität getestet; diese Eigenschaft
läßt sich in manchen, aber nicht in allen Fällen nachweisen. Mit der
multi component theory of perception (MCTP) von Rumelhart läßt sich
erfolgreich vorhersagen, in welchen Situationen die D-Multiplikativität
gilt und in welchen nicht. Nun sollen aber zuerst einige Konsequenzen der
oben gegebenen Definition der S-Multiplikativität dargestellt werden.
Aufgrund der Definition der S-Multiplikativität ist jede beliebige
stochastische Matrix multiplikativ bezüglich einer bestimmten Teilmenge ; deshalb müssen bestimmte Bedingungen für die Zusammensetzung
von S eingeführt werden, um die S-Multiplikativität nicht-trivial zu
halten.
SATZ: Sei eine positive
stochastische Matrix ( 
); es sei 
ein Element
außerhalb einer Untermenge 
, so daß für einige 
und
nicht gleichzeitig iSl und kSj gilt. Außerdem sei 
DEFINITION 3: Zwei Teilmengen und 
werden dekomponierbar (decomposable) genannt, wenn iSj
weder iS'l noch kS'j für beliebige l und k impliziert.
Sei nun 
eine Zerlegung von und
die Teilmengen 
seien paarweise dekomponierbar. Dann
sei 
eine stochastische Matrix, für die gilt,
daß P 
-multiplikativ für 
ist. Dann ist P
S-multiplikativ.
Gilt also Dekomponierbarkeit der Teilmengen, dann ist auch die Vereinigung dieser multiplikativen Teilmengen wiederum multiplikativ.
Schließlich läßt sich zeigen, daß die Funktionen u und v, die die S- Unabhängigkeit definieren, eindeutig sind bis auf die Multiplikation mit einer Konstanten.
zurück zu meiner homepage
rainer@zwisler.de