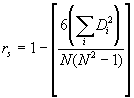Nichtparametrische Tests

Nichtparametrische Tests (oder parameterfreie Tests) werden in folgenden Situationen angewandt:

Wenn die Form der Verteilung (und deren Parameter) unbekannt sind (z.B. keine Normalverteilung bei den Daten);

wenn kein Intervallskalenniveau, sondern nur Ordinalskalenniveau bei den Daten vorliegt.

Der Nachteil solcher Tests liegt in deren geringerer Power. Es folgen einige Beispiele für parameterfreie Tests:

Nichtparametrischer Korrelationskoeffizient

Bei diesem Test -- der Rangkorrelation nach Spearman -- werden die Unterschiede in den Rangplätzen der beiden zusammengehörigen Werte eines Wertepaares betrachtet. Deshalb muß eine abhängige Strichprobe vorliegen, wenn man diesen Test anwenden will. Die Rangkorrelation nach Spearman läßt sich in Worten folgendermaßen präzise formulieren:

r_s = Korrelation zwischen den Rängen über die Individuen.

Wenn keine Übereinstimmungen (ties) bei den Wertepaaren vorliegen, kann folgende einfache Formel zur Berechnung der Korrelation angeben:

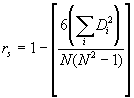wobei D_i die Differenz zwischen den Rängen des Wertepaares i und N die Anzahl der Individuen bezeichnet. Die Hypothese der Unabhängigkeit der beiden Gruppen (also die Frage nach der Signifikanz der Korrelation) läßt sich ebenfalls mit Hilfe des Korrelationskoeffizienten überprüfen; dieser Test besitzt die folgende Form:

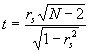Der t-Wert ist mit N - 2 Freiheitsgraden verteilt, wobei N größer als 10 sein sollte. Die Rangkorrelation nach Spearman läßt sich mit dem Kommando rankrel berechnen:

rankrel < grgew.dat

Folgender Teil des Outputs ist dabei relevant:

Spearman Rank Correlation (rho) [corrected for ties]:

Critical r (.05) t approximation        0.373886
Critical r (.01) t approximation        0.478511
rho                                     0.755353

Der Output ist folgendermaßen zu interpretieren: Critical r (.05) t approximation gibt den Wert an, den die Korrelation mindestend erreichen muß, um bei einem Alpha-Niveau von 0.05 signifikant zu sein; Critical r (.01) t approximation nennt den entsprechenden Wert für ein alpha-Niveau von 0.01. rho gibt dann der Wert der Korrelation selbst an, der mit den beiden zuvor beschriebenen Werten verglichen werden kann.

Nichtparametrische Entsprechung zum t-Test für abhängige Stichproben

Eine parameterfreie Entsprechung zum t-Test für abhängige Stichproben ist der Wilcoxon-Test; dieser Test betrachtet nicht nur die Richtung der Unterschiede zwischen den Wertepaaren (also deren Vorzeichen), sondern auch die Höhe der Abweichung. Die Power dieses Tests ist relativ gut; es handelt sich um den "besten" Test für abhängige Stichproben. Grundprinzip: Die Differenzen der Wertepaare werden aufgrund ihrer absoluten Größe in eine Rangreihe gebracht. Dann wird das Vorzeichen der Differenz dem Rangplatz hinzugefügt. Die Teststatistik ist T, die Summe der Ränge mit dem weniger häufigen Vorzeichen.

Die getestete Hypothese ist, daß sich die beiden Populationen, aus denen die Werte der Wertepaare stammen, nicht unterscheiden: Wenn dies der Fall ist, dann ist es für jeden Rangplatz gleich wahrscheinlich, daß ihm ein positives oder negatives Vorzeichen zugewiesen wird. Auf dieser Grundlage läßt sich die exakte Verteilung von T für alle möglichen Randomisierungen bestimmen; für große Stichproben mit dem Umfang N ist die Stichprobe approximativ normalverteilt mit

so daß der Test für eine größere Stichprobe folgendermaßen aussieht:

Dieser Test kann entweder gerichtet oder ungerichtet sein (die für einen gerichteten Test notwendige Normalverteilungs-Annahme macht erst ab einer Stichprobengröße über 8 Sinn). Der Wilcoxon-Test wird bei Verwendung des Kommandos rankrel durchgeführt. Beispiel rankrel < pain.dat Es entsteht folgender Output:

             N      Min      25%   Median      75%      Max
Cond-1      14     1.40     2.10     2.40     2.90     3.20
Cond-2      14     1.40     2.90     3.15     4.40     5.30
Total       28     1.40     2.30     2.90     3.20     5.30

Binomial Sign Test:
Number of cases Cond-1 is above Cond-2:   0
Number of cases Cond-1 is below Cond-2:  10
One-tail probability (exact)            0.000977

Wilcoxon Matched-Pairs Signed-Ranks Test:
Comparison of Cond-1 and Cond-2
T (smaller ranksum of like signs)       0.000000
N (number of signed differences)       10.000000
z                                       2.752095

One-tail probability approximation      0.002961
NOTE: Yates' correction for continuity applied
Check a table for T with N = 10

Friedman Chi-Square Test for Ranks:
Chi-square of ranks                     7.142857
chisq       7.142857     df   1      p  0.007526
Check a table for Friedman with N = 14

Spearman Rank Correlation (rho) [corrected for ties]:
Critical r (.05) t approximation        0.532413
Critical r (.01) t approximation        0.661376
rho                                     0.491695

In diesem Beispiel ergibt sich ein z-Wert von etwa 2.75 (p = 0.003); das Ergebnis des Tests ist somit hoch signifikant.

Hausaufgabe 6 ist zu bearbeiten.

Weitere parameterfreie Verfahren

Bisher haben wir dir Rangkorrelation nach Spearman und den Wilcoxon-Test kennengelernt; für diese beiden Tests wird das Kommando rankrel verwendet. Mit diesem Kommando lassen sich außerdem die folgenden Tests berechnen:

Der binomiale Vorzeichentest wird in Situationen verwendet, in denen N Paare von zusammengehörigen Beobachtungen vorliegen. Folgende Frage soll beantwortet werden: Ist auf lange Sicht die Verteilung der Werte der ersten Stichprobe gleich der Verteilung der Werte der zweiten Stichprobe, wenn alle möglichen Paare betrachtet werden könnten? Für alle Fälle, in denen die Differenz zwischen dem ersten und dem zweiten Wert positiv ist, wird ein "+" gemerkt, für die Fälle, in denen die Differenz negativ ist, ein "-". Sind die beiden Verteilungen wirklich gleich, sollte sich langfristig eine Wahrscheinlichkeit p(+) = p(-) = 0.5 ergeben. Um Aussagen zu der Hypothese p = 0.5 zu erhalten, wird die Wahrscheinlichkeit dafür berechnet, daß in einem Bernoulli-Prozeß so extreme oder extremere Ergebnisse erhalten werden, wenn p tatsächlich 0.5 ist. Ist diese Wahrscheinlichkeit genügend klein (z.B. < 0.05), wird die Hypothese p = 0.5 abgelehnt; dies impliziert, daß auch nicht von einer gleichen Verteilung ausgegangen werden kann. In unserem Beispiel ist das der Fall:

Binomial Sign Test:

Number of cases Cond-1 is above Cond-2: 0 Number of cases Cond-1 is below Cond-2: 10 One-tail probability (exact) 0.000977

Von den 14 Datenpaaren sind 4 genau gleich und in 10 Fällen ist der Wert in Gruppe 2 größer (in keinem Fall ist der Wert in Gruppe 1 größer).

Friedman´s Chi-Quadrat-Test für Ränge kann für J abhängige Gruppen berechnet werden. Es handelt sich um eine Erweiterung des Wilcoxon-Tests für abhängige Stichproben. Dieser Test kann angewendet werden, wenn K Mengen abhängiger Versuchspersonen vorliegen, wobei jede Menge aus J Versuchspersonen besteht, die zufällig einer der J Treatment-Bedingungen zugewiesen wurden. Der Test kann auch verwendet werden, wenn K Versuchspersonen J verschiedenen Treatments unterworfen werden. Die Daten werden in einer Tabelle angeordnet, in der jede Zelle eine einzelne experimentelle Beobachtung enthält. Die Zeilen entsprechen den K (Mengen an) Versuchspersonen, die Spalten den J Treatments:

	Treatment J₁	Treatment J₂	Treatment J₃
VP K₁	x11	x12	< P ALIGN="CENTER">x13
VP K₂	x21	x22	x23
VP K₃	x31	x32	x33
Summe Ränge	s1	s2	s3

Für jede Zeile werden die Rangplätze berechnet und diese werden dann spaltenweise aufaddiert. Dahinter steckt folgende Idee: In einer Population (die durch eine Zeile dargestellt ist), in der das Treatment keinen Effekt hat, sollten sich die Rangplätze zufällig verteilen; auf lange Sicht (wenn man über die verschiedenen Zeilen für die einzelnen Treatmentgruppen aufsummiert) sollten sich dann für alle Gruppe etwa gleiche Summen ergeben, da die verschiedenen Permutationen etwa gleich oft auftreten sollten. Aus den einzelnen Gruppen-Summen läßt sich eine Chi-Quadrat verteilte Prüfgröße errechen (Chi-square of ranks). In unserem Beispiel erhält man folgende Werte:

Friedman Chi-Square Test for Ranks:
Chi-square of ranks                     7.142857
chisq       7.142857     df   1      p  0.007526
Check a table for Friedman with N = 14

Die Anzahl der Freiheitsgrade entspricht der Anzahl der Treatment-Stufen - 1.

Nichtparametrische Entsprechung zum t-Test für unabhängige Stichproben

Das Kommando rankind führt einige parameterfreie Tests durch. Die Daten müssen für jede Gruppe durch einen splitter getrennt werden (wie bei dem Kommando oneway). Neben verschiedenen deskriptiven Statistiken werden folgende Signifikanztests gerechnet:

Median-Test (Fisher´s exact Test)

Mann-Whitney´s U-Test

Varianzanalyse für Ränge nach Kruskal-Wallis

Die folgende Eingabe

rankind < coffee2.dat

führt zu diesem Output:

             N      Min      25%   Median      75%      Max
Cond-1      10   179.00   188.00   194.50   201.00   215.00
Cond-2      10   189.00   199.00   214.50   221.00   231.00
Total       20   179.00   190.50   200.00   215.00   231.00

Median-Test:
Fisher Exact One-Tailed Probability     0.089448
Fisher Exact Other-Tail Probability     0.089448
Fisher Exact Two-Tailed Probability     0.178895
       Cond-1 Cond-2
above       3      7     10
below       7      3     10
           10     10     20
NOTE: Yates' correction for continuity applied
chisq       1.800000     df   1      p  0.179712

Mann-Whitney U:
U                                      81.000000
U'                                     19.000000
z(U) (corrected for ties)               2.344262
One tailed p(z(U))                      0.009532
Check a table for U with n = 10

Kruskal-Wallis:
H (not corrected for ties)              5.491429
Tie correction factor                   0.998496
H (corrected for ties)                  5.499699
chisq       5.499699     df   1      p  0.019020
Check a table for Kruskal-Wallis H

Bei den hier vorliegenden Daten handelt es sich um Reaktionszeiten. Diese sind nicht normalverteilt. Deshalb ist der Median ein adäquateres Maß der zentralen Tendenz als das arithmetische Mittel. Folgende Tests wurden im einzelnen berechnet:

Der Median-Test wird auch als Fisher´s exakter Test bezeichnet, dem folgender Grundgedanke zugrunde liegt: Wenn eine Stichprobe aus zwei identisch verteilten Populationen gezogen wurde (also eigentlich aus einer Population stammt), wird die kombinierte Stichprobe homogen sein; man kann deshalb die zwei Stichproben als zufällig aus einer kleinen Gesamtpopulation, nämlich der kombinierten Stichprobe, (ohne Zurücklegen) gezogen betrachten. Es wird getestet, ob sich die beiden Teilstichproben nur zufällig voneinander unterscheiden. Die dem Test zugrundeliegende Nullhypothese ist somit die folgende: Teilstichprobe 1 ist eine Zufallsstichprobe (die ohne Zurücklegen gezogen wurde) aus der kombinierten Stichprobe. Der Umfang der beiden unabhängigen Stichproben muß für diesen Test nicht gleich sein.

Zuerst wird der Gesamt-Median der gepoolten Stichprobe berechnet (bei geradzahligem Umfang der Gesamtstichprobe wird das arithmetische Mittel aus den beiden mittleren Werten als Median verwendet). Dann werden die beiden Werte

a₁ = Anzahl der Werte über dem Median in Stichprobe 1 und

a₂ = Anzahl der Werte über dem Median in Stichprobe 2

berechnet. Damit läßt sich für die erste Stichprobe die binomiale Wahrscheinlichkeit dafür berechnen, daß genau a₁ aus den N₁ Beobachtungen über dem Median liegen: 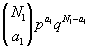; analog läßt sich die Wahrscheinlichkeit für die zweite Stichprobe berechnen. Da man die beiden Stichproben als unabhängig betrachten kann, errechnet sich die gemeinsame Wahrscheinlichkeit dafür, daß a₁ und a₂ Werte über dem Median erhalten werden, aus dem Produkt der Einzelwahrscheinlichkeiten. In diesem Fall interessiert allerdings die bedingte Wahrscheinlichkeit dafür, daß a₁ + a₂ Werte über dem Median bei N₁ + N₂ Beobachtungen erhalten werden; sie läßt sich folgendermaßen errechnen:

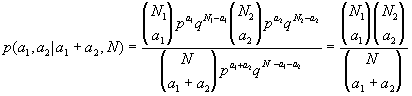Man testet hiermit, ob die Werte von a₁ so extrem sind, daß ihr Auftreten unter der Bedingung, daß die beiden Stichproben gleich verteilt sind, extrem unwahrscheinlich wird (gleiches gilt für a₂); solche Extremfälle führen dazu, die Nullhypothese zu verwerfen. Für den Test selbst wird eine Chi-Quadrat-verteilte Prüfgröße betrachtet. Das Ergebnis des Test sieht so aus:

Median-Test:
Fisher Exact One-Tailed Probability     0.089448
Fisher Exact Other-Tail Probability     0.089448
Fisher Exact Two-Tailed Probability     0.178895
       Cond-1 Cond-2
above       3      7     10
below       7      3     10
           10     10     20
NOTE: Yates' correction for continuity applied
chisq       1.800000     df   1      p  0.179712

Beim Mann-Whitney U-Test werden direkt die Ränge der einzelnen Beobachtungen verrechnet. Dieser Test besitzt im allgemeinen gegenüber dem Mediantest eine deutlich größere Power. Die Wahrscheinlichkeits-Aussagen beziehen sich direkt auf alle möglichen Randomisierungen der selben Stichprobe von N Versuchspersonen unter verschiedenen Treatments. Nullhypothese ist, daß beide zu vergleichende Populationen gleich verteilt sind. Die Werte der kombinierten Stichproben werden in eine einzige Rangreihe gebracht, wobei jeder der Beobachtungen ein Rang zugewiesen wird. Dann werden die Ränge für die einzelnen Stichproben aufsummiert (T₁ für die erste Stichprobe, T₂ für die zweite); diese Rangsummen sollten etwa gleich groß sei, wenn beide Stichproben aus der selben Population stammen und dem Erwartungswert der Ränge entsprechen. Nun lassen sich zwei Größen berechnen:

; ist U größer als N₁N₂/2, nimmt man

Die verwendete Statistik ist der kleinere der beiden Werte U und U´. Diese Statistik ist normalverteilt; man erhält somit eine z-verteilte Prüfgröße. In unserem Beispiel erhalten wir:

Mann-Whitney U:
U                                      81.000000
U'                                     19.000000
z(U) (corrected for ties)               2.344262
One tailed p(z(U))                      0.009532
Check a table for U with n = 10

Auch hier liegt ein hochsignifikantes Ergebnis vor (p = 0.0095).

Die parameterfreie Varianzanalyse nach Kruskal-Wallis ist eine Erweiterung des U-Tests von Mann-Whitney. Auch hier werden die Scores aller J unabhängigen Gruppen gepoolt, nach der Größe sortiert und Rangplätzen zugewiesen; die Ränge beziehen sich also auf die Gesamtstichprobe. Dann wird die Rangsumme für jede einzelne Gruppe gebildet (T_j = Rangsumme für Gruppe j). Da es sich um unterschiedliche Gruppengrößen handeln kann, müssen diese Summen noch an der Gruppengröße relativiert werden. Für die Prüfgröße H gilt folgende Formel:

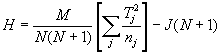Kommen gleiche Werte (ties) vor, muß noch eine Korrektur erfolgen:

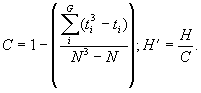
Dabei ist G die Anzahl der Gleichstände und t_i die Anzahl der Gleichstände in einer Gruppe i. Der für H errechnete Wert ist Chi-Quadrat-verteilt mit J - 1 Freiheitsgraden (bei der Nullhypothese, daß sich die Gruppen nicht unterscheiden). Für das angegebene Beispiel erhält man:

Kruskal-Wallis:

H (not corrected for ties) 5.491429 Tie correction factor 0.998496 H (corrected for ties) 5.499699 chisq 5.499699 df 1 p 0.019020 Check a table for Kruskal-Wallis H

Chi-Quadrat-Unabhängigkeitstest

Jede einzelne Beobachtung wird dabei in nur eine Kategorie der ersten Variable oder in eine Kategorie der zweiten Variable eingeordnet (landet also genau in einem der vier Felder). Die Daten liegen also in folgendem Format vor:

a	b	a + b
c	d	c + d
a + c	b + d	N

Die Kleinbuchstaben a, b, c und d repräsentieren die Häufigkeiten in den einzelnen Zellen. Der Wert für c ² läßt sich dann auf folgende Art bestimmen:

(mit einem Freiheitsgrad).

Dieser Wert wird normalerweise mit der Yates´ correction for continuity korrigiert, um eine bessere Annäherung an die exakte multinomiale Wahrscheinlichkeit zu erhalten (diese Korrektur sollte nur angewandt werden, wenn genau ein Freiheitsgrad vorliegt). Mit der Korrektur wird der Wert nach folgender Formel gefunden:

Für den Chi-Quadrat-Unabhängigkeitstest wird dann das Kommando contab verwendet. In der Datendatei stehen genau vier Zeilen; jede Zeile enthält drei Einträge:

Die Ausprägung der ersten Variable (Label);

die Ausprägung der zweiten Variable (Label) und

die abhängige Variable (Häufigkeit für die jeweilige Kategorie).

Eine Beispielsdatei (4feld.dat) sieht dementsprechend folgendermaßen aus:

raucher trinker  30
raucher antialk  10
nonsmoke trinker 8
nonsmoke antialk 16

Damit läßt sich beispielsweise feststellen, ob die beiden Verhaltensweisen Rauchen und Trinken voneinander unabhängig sind:

contab < 4feld.dat

Es wird folgender Output erzeugt:

FACTOR:          A          B       DATA
LEVELS:          2          2         64

A          count
raucher       40
nonsmoke      24
Total         64
NOTE: Yates' correction for continuity applied
chisq       3.515625     df   1      p  0.060793

B          count
trinker       38
antialk       26
Total         64
NOTE: Yates' correction for continuity applied
chisq       1.890625     df   1      p  0.169131

SOURCE: A B
         trinker antialk  Totals
raucher       30      10      40
nonsmoke       8      16      24
Totals        38      26      64
Analysis for A x B:
NOTE: Yates' correction for continuity applied
chisq       9.137922     df   1      p  0.002504
Fisher Exact One-Tailed Probability     0.001212
Fisher Exact Other-Tail Probability     0.000329
Fisher Exact Two-Tailed Probability     0.001541
phi Coefficient == Cramer's V           0.377862
Contingency Coefficient                 0.353470

Zuerst wird also für jede der beiden Variablen ein Mediantest berechnet; schließlich wird der Chi-Quadrat-Unabhängigkeitstest durchgeführt. Folgende Begriffe bedürfen noch einer Erklärung:

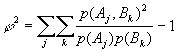phi-Koeffizient: Die mittlere quadratische Kontingenz (mean square contingency) ist für eine Tabelle mit R Zeilen und C Spalten folgendermaßen definiert:

;

dieser Populationsindex kann nur dann Null werden, wenn komplette Unabhängigkeit vorliegt (wenn also ). Für eine Menge an Daten, die in einer RxC-Tabelle stehen, läßt sich der Koeffizient der Stichprobe einfach berechnen. Cramer´s Statistik, deren Wert zwischen 0 und 1 liegen muß, beschreibt die in der Stichprobe vorliegende Stärke der Assoziation:

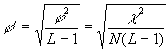(wobei L die kleinere der beiden Zahlen R und C ist).

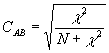
Kontingenz-Koeffizient: Dieser Koeffizient ist durch folgende Formel definiert:

zurück zur Hauptseite zum Seminar "Rechnergestützte Auswertung von psychologischen Experimenten"

Anmerkungen und Mitteilungen an