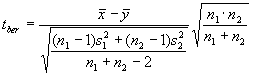Tests für metrische Daten

Das Kommando pair

pair dient zur Berechnung von Pearson´s Produkt-Moment-Korrelation und von t-Tests für abhängige Stichproben. Input sind eine Reihe von jeweils zwei Zahlen pro Zeile. Es werden zusammenfassende Statistiken und Signifikanztests für die beiden Input-Variablen und deren Differenz berechnet, sowie Korrelation, einfache lineare Regression; außerdem ist eine graphische Darstellung möglich.

Ein Beispiel wäre die Berechnung der Korrelation zwischen Größe und Gewicht. Das Inputformat unserer Datei grgew.dat hat zwei Spalten und paßt somit genau für pair:

pair < grgew.dat

Analysis for 18 points:
                         Column 1         Column 2       Difference
Minimums                 165.0000          51.0000          85.0000
Maximums                 197.0000          91.0000         122.0000
Sums                    3152.0000        1220.0000        1932.0000
SumSquares            553262.0000       85604.0000      208956.0000
Means                    175.1111          67.7778         107.3333
SDs                        8.7843          13.0949           9.6650
t(17)                     84.5754          21.9594          47.1162
p                          0.0000           0.0000           0.0000
 
     Correlation        r-squared            t(16)                p
          0.6747           0.4553           3.6568           0.0021
       Intercept            Slope
       -108.3568           1.0058

• Correlation (Korrelationskoeffizient) ;
• r-squared (Determinationskoeffizient, erklärte Varianz) r²;
• p (Signifikanztest)
• t(16) (Die t-verteilte Prüfgröße zur Beurteilung der Signifikanz der Korrelation; hier liegen nur 16 Freiheitsgrade vor, da sowohl ein Wert für die Größe als auch einer für das Gewicht nicht frei wählbar ist).
• Intercept und Slope (Nulldurchgang und Steigung der Regressionsgleichung):

• Column 1 (unterscheiden sich die Werte in s1 von Null);
• Column 2 (unterscheiden sich die Werte in s2 von Null);
• Difference (unterscheiden sich die Differenzen der Wertepaare von Null); Formel:

Dieser t-Test darf nicht mit der Datei rats.dat gerechnet werden, da dort unterschiedliche Versuchstiere verwendet wurden und somit eine unabhängige Stichprobe vorliegt.

Das Kommando oneway

Eine Formel zur praktischen Berechnung (Bosch, Elementare Einführung in die angewandte Statistik, S.88) wäre die folgende:

;

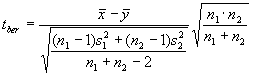aufgrund dieser aus den beiden Stichproben berechneten Prüfgröße ergeben sich dann mit der t-Verteilung mit n₁ + n₂ - 2 Freiheitsgraden die Testentscheidungen.

Für diese Programm ist ein ganz bestimmtes Inputformat erforderlich: Zuerst müssen die Werte für Gruppe 1 zeilenweise (also genau ein Element pro Zeile) aufgeführt werden, dann muß ein Splitter folgen (normalerweise die Zahl -1), dann erst die Werte für Gruppe 2 usw. Folgendes Beispiel mit der Beispieldatei ttest.dat soll dies veranschaulichen; sie ist folgendermaßen aufgebaut:

7
10
12
13
-1
7
9
13
16
15

oneway -t -p < ttest.dat | more

Name          N     Mean       SD      Min      Max
Group-1       5   10.200    2.387    7.000   13.000
Group-2       5   12.000    3.873    7.000   16.000
Total        10   11.100    3.178    7.000   16.000
 
Group-1   |<----=========(======#======)=========->                    |
Group-2   |<------==============(===========#==========)==============>|
           7.000                                                 16.000
 
Weighted Means Analysis:
t(8) = 0.885   p = 0.402