Vorbemerkung zur Erzeugung der Datenfiles: Mit dem Kommando abut kann man Datenfiles erzeugen, die aus mehreren Spalten bestehen und in denen sich unter Umständen gewisse Spalteneinträge wiederholen. Wichtig sind die Optionen
hour1 hour24Ebenso erstellt man die Datei file2.dat, die die Menge an Futter (Belohnung) enthält:
grape1 grape3 grape5Schließlich erzeugt man mit dem Kommando
series 1 24 > nums.dateine Datei nums.dat, in der die Zahlen von 1 bis 24 in jeweils einer Zeile stehen (diese wird benötigt anstelle der Option -n von abut, da ja die Länge der anderen Dateien netsprechend erweiter werden muß). Den Vorläufer der gewünschten Datei monkey1.dat erhält man dann mit folgender Eingabe:
abut -c nums file1 file2 > monkey1.datIn diese Datei müssen dann noch jeweils ans Ende der Zeilen die Rohwerte eingetragen werden; dazu kann man beispielsweise den DOS-Editor edit verwenden. Die entsprechend aufbereitete Datei monkey1.dat sollte etwa so aussehen:
1 hour1 grape1 1 2 hour1 grape1 4 3 hour1 grape1 0 4 hour1 grape1 7 5 hour1 grape3 13 6 hour1 grape3 5 7 hour1 grape3 7 8 hour1 grape3 15 9 hour1 grape5 9 10 hour1 grape5 16 11 hour1 grape5 18 12 hour1 grape5 13 13 hour24 grape1 15 14 hour24 grape1 6 15 hour24 grape1 10 16 hour24 grape1 13 17 hour24 grape3 6 18 hour24 grape3 18 19 hour24 grape3 9 20 hour24 grape3 15 21 hour24 grape5 14 22 hour24 grape5 7 23 hour24 grape5 6 24 hour24 grape5 13Die geeignete zweifaktorielle Varianzanalyse wird mit folgender Zeile gestartet
anova monkey deprivation fruit behavior < monkey1.datund liefert diesen Output:
SOURCE: grand mean
depriva fruit N MEAN SD SE
24 10.0000 5.1499 1.0512
SOURCE: deprivation
depriva fruit N MEAN SD SE
hour1 12 9.0000 5.9696 1.7233
hour24 12 11.0000 4.1996 1.2123
SOURCE: fruit
depriva fruit N MEAN SD SE
grape1 8 7.0000 5.3984 1.9086
grape3 8 11.0000 4.8697 1.7217
grape5 8 12.0000 4.2762 1.5119
SOURCE: deprivation fruit
depriva fruit N MEAN SD SE
hour1 grape1 4 3.0000 3.1623 1.5811
hour1 grape3 4 10.0000 4.7610 2.3805
hour1 grape5 4 14.0000 3.9158 1.9579
hour24 grape1 4 11.0000 3.9158 1.9579
hour24 grape3 4 12.0000 5.4772 2.7386
hour24 grape5 4 10.0000 4.0825 2.0412
FACTOR: monkey deprivatio fruit behavior
LEVELS: 24 2 3 24
TYPE : RANDOM BETWEEN BETWEEN DATA
SOURCE SS df MS F p
===============================================================
mean 2400.0000 1 2400.0000 130.909 0.000 ***
m/df 330.0000 18 18.3333
depriva 24.0000 1 24.0000 1.309 0.268
m/df 330.0000 18 18.3333
fruit 112.0000 2 56.0000 3.055 0.072
m/df 330.0000 18 18.3333
df 144.0000 2 72.0000 3.927 0.038 *
m/df 330.0000 18 18.3333
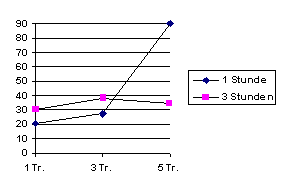
Diese Mittelwerte sehen folgendermaßen aus:

Interessant zu bemerken ist hier, daß weder die Dauer der Deprivation noch die Höhe der Belohnung für sich genommen einen signifikanten Einfluß ausüben (Höhe der Belohnung aber fast); die Interaktion zwischen den beiden Faktoren ist dagegen schon signifikant.
Die Varianzanalyse für die Replikation des Experimentes erfordert wiederum eine entsprechende Aufbereitung der Daten; sie sind diesmal in der Datei monkey2.dat gespeichert. Die Varianzanalyse wird folgendermaßen gestartet:
anova monkey deprivation fruit behavior < monkey2.datund sie liefert folgenden Output:
SOURCE: grand mean
depriva fruit N MEAN SD SE
24 10.0000 6.1715 1.2597
SOURCE: deprivation
depriva fruit N MEAN SD SE
hour1 12 9.0000 6.5227 1.8829
hour24 12 11.0000 5.9084 1.7056
SOURCE: fruit
depriva fruit N MEAN SD SE
grape1 8 7.0000 6.7612 2.3905
grape3 8 11.0000 5.8554 2.0702
grape5 8 12.0000 5.3984 1.9086
SOURCE: deprivation fruit
depriva fruit N MEAN SD SE
hour1 grape1 4 3.0000 4.6904 2.3452
hour1 grape3 4 10.0000 5.2915 2.6458
hour1 grape5 4 14.0000 4.8305 2.4152
hour24 grape1 4 11.0000 6.4807 3.2404
hour24 grape3 4 12.0000 7.0238 3.5119
hour24 grape5 4 10.0000 5.8310 2.9155
FACTOR: monkey deprivatio fruit behavior
LEVELS: 24 2 3 24
TYPE : RANDOM BETWEEN BETWEEN DATA
SOURCE SS df MS F p
===============================================================
mean 2400.0000 1 2400.0000 72.483 0.000 ***
m/df 596.0000 18 33.1111
depriva 24.0000 1 24.0000 0.725 0.406
m/df 596.0000 18 33.1111
fruit 112.0000 2 56.0000 1.691 0.212
m/df 596.0000 18 33.1111
df 144.0000 2 72.0000 2.174 0.143
m/df 596.0000 18 33.1111
Auch diese Ergebnis läßt sich folgendermaßen visualsieren:

Hier ist keiner der beiden Faktoren signifikant; auch die Interaktion ist es nicht. Auffällig ist, daß die einzelnen Gruppenmittelwerte die genau selben sind wie im ersten Experiment, aber die Varianzen nicht (dies weist darauf hin, daß für das Ergebnis einer Varianzanalyse nicht die Mittelwerte, sondern - wie der Name schon sagt - die Varianzen wichtig sind). Die in diesem Fall höheren Fehlervarianzen führen dazu, daß das Ergebnis der Varianzanalyse nicht signifikant ist.
zurück zur Hauptseite zum Seminar "Rechnergestützte Auswertung von psychologischen Experimenten"
Anmerkungen und Mitteilungen an
rainer@zwisler.de