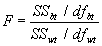
Bisher lag immer eine unabhängige Variable in verschiedenen Ausprägungen (Faktorstufen) vor. Beispiel rats.dat. Fragen:
Es wäre auch möglich, den Einfluß dieser beiden Faktoren in getrennten Studien zu untersuchen. Ein zweifaktorielles Design bietet aber zwei wesentliche Vorteile:
Folgendes Ergebnis für unser oben genanntes Beispiel wäre möglich:
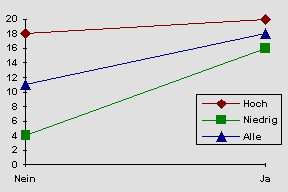
Hier liegen also eigentlich mehrere Graphen (einer für die hohe und einer für die niedrige soziale Schicht; zusätzlich noch einer für alle zusammen) in einem vor. Fragen:
Jetzt lassen sich folgende drei Fragen beantworten:
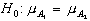) Im Klartext: Gibt es Unterschiede zwischen den Stufen von Faktor A, wenn ich über die Stufen von Faktor B mittele (hat also das Lernprogramm einen Effekt, unabhängig davon, aus welcher Schicht der Betrachter kommt)? Antwort: Ja (die mittlere Linie im Graph steigt).
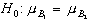) Im Klartext: Gibt es Unterschiede zwischen den Stufen von B, wenn ich über die Stufen von A mittele (also einen Einfluß der sozialen Schicht alleine)? Antwort: Ja (die B2 Kurve liegt immer über der B1-Kurve).
Verständnisfrage: Wie sähe der Graph aus, wenn Schichtzugehörigkeit keinen Einfluß auf den Effekt des Programms hätte? Antwort: Linie für hohe und niedrige Schicht wären gleich.
Die Unterteilung der Gesamtvarianz SSTotal in die Varianz innerhalb der Gruppen SSWT und die Varianz zwischen den Gruppen SSBT bleibt so wie bei der einfaktoriellen Varianzanalyse; der Treatmenteffekt wird jedoch weiter aufgegliedert in die Varianzen SSA , SSB und SSAxB.
Daraus ergeben sich drei F-Werte: FA, FB und FAxB. Diese sind alle auf Signifikanz zu prüfen.
Es werden alle Daten benötigt sowie die Informationen darüber, in welche Zelle des Designs das jeweilige Datum gehört (mit man anova genauer). Das Programm bestimmt dann selbst, ob die Daten konsistent eingegeben wurden (keine Leerzeilen) und welche Art der Varianzanalyse die richtige ist (je nachdem, ob ein Design mit oder ohne Meßwiederholungen (between and within subjects design) vorliegt, muß nämlich unterschiedlich gerechnet werden).
Von Meßwiederholung spricht man dann, wenn von der selben Versuchsperson mehrere Daten erhoben werden; der Faktor Versuchsperson wird dann von anova als RANDOM klassifiziert, der wiederholt gemessene Faktor als WITHIN und der Faktor, der zwischen den Versuchspersonen unterschiedlich ist, als BETWEEN. Diese Einteilung übernimmt das Programm anova selbstständig aufgrund der in den Daten enthaltenen Versuchspersoneninformation (üblicherweise steht deshalb in der ersten Spalte ein Versuchspersonencode, also eine Identifikation der Versuchsperson).
Ein Beispiel für eine Varianzanalyse mit Meßwiederholung wird später folgen (wahrscheinlich erst in der nächsten Stunde).
Es geht um folgendes Problem: Wie wirken drei verschiedene Medikamente bei zwei Kategorien von Patienten, um psychotische Symptome zu reduzieren? Abhängige Variable ist das Rating der Verbesserung des Patienten; unabhängige Variablen sind:
1 schizo med1 8 2 schizo med1 4 3 schizo med1 0 4 depr med1 14 5 depr med1 10 6 depr med1 6 7 schizo med2 10 8 schizo med2 8 9 schizo med2 6 10 depr med2 4 11 depr med2 2 12 depr med2 0 13 schizo med3 8 14 schizo med3 6 15 schizo med3 4 16 depr med3 15 17 depr med3 12 18 depr med3 9
Die vier Spalten sind folgendermaßen zu interpretieren:
anova vp diag med bess < drugs.datDie vier Argumente, mit denen das Programm anova aufgerufen wird, geben die Bezeichnungen an, die für die Spalten des Outputfiles verwendet werden sollen (wie sollen die Variablen vom Programm bezeichnet werden?). anova liefert dann folgenden Output:
SOURCE: grand mean
diag med N MEAN SD SE
18 7.0000 4.3114 1.0162
SOURCE: diag
diag med N MEAN SD SE
schizo 9 6.0000 3.0000 1.0000
depr 9 8.0000 5.3151 1.7717
SOURCE: med
diag med N MEAN SD SE
med1 6 7.0000 4.8580 1.9833
med2 6 5.0000 3.7417 1.5275
med3 6 9.0000 4.0000 1.6330
SOURCE: diag med
diag med N MEAN SD SE
schizo med1 3 4.0000 4.0000 2.3094
schizo med2 3 8.0000 2.0000 1.1547
schizo med3 3 6.0000 2.0000 1.1547
depr med1 3 10.0000 4.0000 2.3094
depr med2 3 2.0000 2.0000 1.1547
depr med3 3 12.0000 3.0000 1.7321
FACTOR: vp diag med bess
LEVELS: 18 2 3 18
TYPE : RANDOM BETWEEN BETWEEN DATA
SOURCE SS df MS F p
===============================================================
mean 882.0000 1 882.0000 99.849 0.000 ***
v/dm 106.0000 12 8.8333
diag 18.0000 1 18.0000 2.038 0.179
v/dm 106.0000 12 8.8333
med 48.0000 2 24.0000 2.717 0.106
v/dm 106.0000 12 8.8333
dm 144.0000 2 72.0000 8.151 0.006 **
v/dm 106.0000 12 8.8333
Es ergaben sich also die folgenden Gruppenmittelwerte:
|
med1 |
med2 |
med3 |
Mittelmed |
|
|
schizophren |
4 |
8 |
6 |
6 |
|
depressiv |
10 |
2 |
12 |
8 |
|
Mittelmed |
7 |
5 |
9 |
7 |
Graphisch läßt sich dieser Zusammenhang folgendermaßen darstellen:
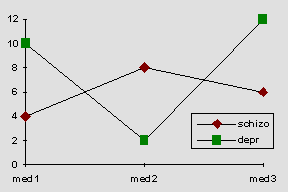
Feststellung einer Interaktion: Folgender Teil des Outputs bezieht sich auf die Interaktion der beiden Faktoren diag und med (deshalb auch die Abkürzung dm):
dm 144.0000 2 72.0000 8.151 0.006 **
v/dm 106.0000 12 8.8333
Es liegt eine signifikante Wechselwirkung vor: F(2;12) = 8.151, p < 0.01 (nämlich 0.006). Die Freiheitsgrade für den F-Wert lassen sich folgendermaßen erläutern (p = Anzahl der Faktorstufen A; q = Anzahl der Faktorstufen B; N = Stichprobenumfang):
Graphisch läßt sich die Interaktion auch zeigen: Die Differenz der Mittelwerte der schizophrenen Gruppe (6) und der depressiven Gruppe (8) beträgt -2. Wenn sich alle drei Medikamente bei den verschiedenen Krankheiten gleich auswirken, muß jeweils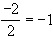 
(also Differenz durch Anzahl der Gruppen teilen) von den Gruppenmittelwerten für Medikament1, Medikament2 und Medikament3 abgezogen werden. Es ergibt sich daraus folgende Tabelle:
|
med1 |
med2 |
med3 |
Mittelmed |
|
|
schizophren |
7 - 1 = 6 |
5 - 1 = 4 |
9 - 1 = 8 |
6 |
|
depressiv |
7 + 1 = 8 |
5 + 1= 6 |
9 + 1 = 10 |
8 |
|
Mittelmed |
7 |
5 |
9 |
7 |
In dieser Tabelle stehen die Zellenmittelwerte, wenn der Faktor A (Patientengruppe) auf allen Stufen des Faktors B (Medikation) gleich wirken würde. In diesem Fall würde keine Interaktion der Faktoren vorliegen, was man auch an den parallelen Geraden in der graphischen Darstellung sieht:
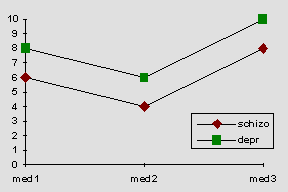
Nebenbemerkung: Wie kann ich die SSAxB berechnen? Die SSAxB läßt sich als Summe der quadrierten Abweichungen der erwarteten Zellenwerte (repräsentiert durch die erwarteten Zellenmittelwerte in der zweiten Tabelle) von den tatsächlichen Zellenwerten berechnen:
SSAxB = 3 * (6 - 4)2 + 3 * (4 - 8)2 + 3 * (8 - 6)2 + 3 * (8 - 10)2 + 3 * (6 - 2)2 + 3 * (10 - 12)2 =
= 144
Fortsetzung der zweifaktoriellen Varianzanalyse
In der Datei develop.dat sind Daten enthalten, mit denen sich eine Varianzanalyse mit Meßwiederholung demonstrieren läßt; diese Datei soll gelesen werden. Das Datenfile develop.dat sieht folgendermaßen aus:Klaus niedrig 63 Gottfried niedrig 210 Erika niedrig 94 Judith niedrig 219 Miriam niedrig 54 Peter niedrig 120 Elisabeth niedrig 195 Klaus mittel 112 Gottfried mittel 73 Erika mittel 314 Judith mittel 232 Miriam mittel 396 Peter mittel 352 Elisabeth mittel 409 Klaus hoch 39 Gottfried hoch 80 Erika hoch 83 Judith hoch 115 Miriam hoch 76 Peter hoch 100 Elisabeth hoch 206
Der Name am Anfang jeder Zeile steht dort, um die jeweilige Person identifizierbar zu machen.
Für eine einfaktorielle Varianzanalyse mit Meßwiederholung muß das Programm anova verwendet werden (oneway ist nicht geeignet, da Meßwiederholung vorliegt). Der Vorteil einer Varianzanalyse mit Meßwiederholung besteht darin, daß die Varianz aufgrund individueller Unterschiede herausfällt (da ja für jede Person alle Meßwerte erhoben werden). Man betrachte dazu beispielsweise folgende Zeilen, in denen der erste Wert für die Bedingung niedrig, der zweite Wert für die Bedingung mittel und der dritte Wert für die Bedingung hoch (bei dem Faktor Komplexitätsgrad) steht:
Beide Personen betrachten den mittleren Komplexitätsgrad am längsten; es liegen aber große Unterschiede in den absoluten Werten vor. Diese Unterschiede gehen alle in die SSwithin ein. Bei einem within-subject-design wird diese Quelle der Varianz aus dem Fehlerterm herausgenommen; die Varianzen unterteilen sich dann folgendermaßen:
Das Kommando
anova kid level time < develop.dat
SOURCE: grand mean
level N MEAN SD SE
21 168.6667 115.6137 25.2290
SOURCE: level
level N MEAN SD SE
niedrig 7 136.4286 70.6136 26.6894
mittel 7 269.7143 134.8292 50.9606
hoch 7 99.8571 52.3559 19.7887
FACTOR: kid level time
LEVELS: 7 3 21
TYPE : RANDOM WITHIN DATA
SOURCE SS df MS F p
===============================================================
mean 597417.3333 1 597417.3333 52.022 0.000 ***
k/ 68903.3333 6 11483.8889
level 111892.6667 2 55946.3333 7.758 0.007 **
lk/ 86534.6667 12 7211.2222
Es ist zu sehen, daß das Programm anova den Faktor level korrekt als within-subjects identifiziert hat. Es besteht außerdem die Möglichkeit, daß ein Faktor within subjects und ein anderer between subjects variiert (z.B. bei Einführung einer weiteren Altersgruppe in develop.txt).
Hausaufgabe: hausauf5.txt bearbeiten.
zurück zur Hauptseite zum Seminar "Rechnergestützte Auswertung von psychologischen Experimenten"
Anmerkungen und Mitteilungen an
rainer@zwisler.de