Lösen komplexer Planungsaufgaben:
Eine experimentelle Untersuchung zum Strategieerwerb
Rainer Zwisler, erstellt am 20.07.93
zurück zur Skriptenseite
zurück zu meiner homepage
Inhaltsverzeichnis
1. Einführung und Problemstellung
1.1. Planen in der KI
1.2. Planen aus psychologischer Sicht
Planung der Steuerung industrieller Prozesse
1.3. Die Fragestellung
Die Herkunft der Aufgabenstellung
Die Klasse der verwendeten Aufgaben
2. Faktoren der Aufgabenbearbeitung
2.2. Mentale Arithmetik
Befunde zu Größenvergleich von Zahlen
Größenvergleich von Zahlen nach Dehaene, Dupoux und Mehler (1990)
Berechnungen mit einstelligen Zahlen
2.3. Work-Load
Der Verlust von Gedächtniselementen
2.4. Strategieerwerb
2.5. Die Problemrepräsentation
2.6. Der Lernfortschritt der Versuchspersonen
2.7. Die Lerntheorie von J. R. Anderson
Compilierung und Prozeduralisierung
2.8. Zusammenfassung
3. Methode
3.1. Material
Formale Aspekte der verwendeten Aufgaben
Die Aufgabenstellung für die Versuchsperson
3.2. Hypothesen
Die geschätzte Distanz zum Optimum
3.3. Design
3.4. Versuchspersonen
3.5. Material
4. Einzelergebnisse und ihre Diskussion
4.1. Die Eingabezeiten
Häufigkeit der Wahl eines Feldes, auf dem nichts mehr vergeben werden kann
4.2. Die Lösungszeiten
Varianzanalytische Betrachtung der Lösungszeiten
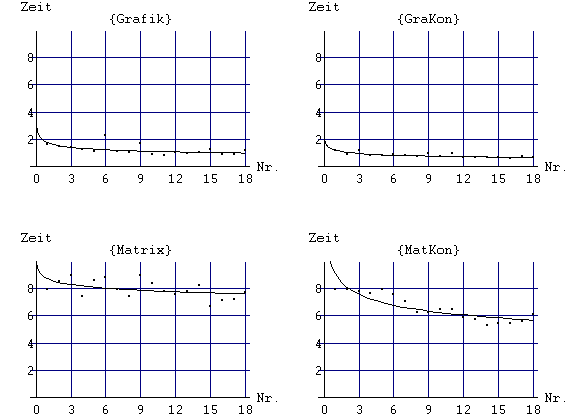
Die Lernkurven (regressionsanalytische Betrachtung)
Die Verteilung der Lösungszeit innerhalb der Aufgaben
Die Korrelation zwischen Lösungszeit und der Anzahl an Schritten
4.3. Die Distanzen zum Optimum
Die Häufigkeit optimaler Lösungen
Die tatsächlichen Distanzen zum Optimum
Die minimale Anzahl der Schritte bei optimaler Strategie
Die durchschnittliche Anzahl der Schritte zur Lösung
4.6. Die Variationen in den Aufgaben
Der Effekt der Aufgabenstruktur
4.7. Die Anwendung von Strategien
Heuristiken zur Verkleinerung des Problemraums
Identifikation der Anwendung der optimalen Strategie
Die Anwendung anderer Strategien
Bildschirmpräsentation und Anwendung der optimalen Strategie
Das Beibehalten der optimalen Strategie
Der Verlauf der Anwendung der optimalen Strategie
4.8. Die Verbalisierung von Strategien
5.2. Der Einfluß des Zahlenmaterials
5.3. Work-Load und Strategie-Erwerb
Kein Strategieerwerb im Experiment
Störung des Strategie-Erwerbs durch hohe Work-Load
Alternative Erklärungen für das Ausbleiben des Strategie-Erwerbs
5.4. Die Problemrepräsentation
Das Display als Erweiterung des Arbeitsgedächtnisses
5.5. Zusammenfassung
6. Erklärung des Verhaltens der Versuchspersonen
6.1. Implizites Lernen
6.2. Die Verminderung der Lösungszeiten
6.3. Das Experiment in Andersonīs Theoriesprache
7. Ausblick
7.1. Noch zu untersuchen
7.2. Die Aufgaben als "Planungsaufgaben"
7.3. Pädagogische Implikationen
Anhang A: Der Bildschirm der Grafik-Bedingung
Anhang B: Der Bildschirm der Matrix-Bedingung
Anhang C: Die Instruktionen der Grafik-Bedingung:
Anhang D: Die Instruktionen der Matrix-Bedingung:
Anhang E: Die Erläuterung der optimalen Strategie
Anhang F: Die nach dem Experiment gestellten Fragen
Anhang G: Die Angebots-Strategie:
Anhang H: Die Bedarfs-Strategie:
Die Tätigkeit des Planens tritt im täglichen Leben häufig auf: Planen kann überwiegend als praktische Aktivität betrachtet werden; daraus läßt sich dann auch die Definition des Begriffs herleiten. Diesen Weg gehen z.B. Hayes-Roth und Hayes-Roth (1979) in ihrer eher psychologischen Definition des Begriffs Planen:
"We define planning as the predetermination of a course of action aimed at achieving some goal. It is the first stage of a two-stage problem-solving process. The second stage entails monitoring and guiding the execution of a plan to a useful conclusion. We refer to these two stages as planning and control" (Hayes-Roth & Hayes-Roth, 1979, S. 275 f, Hervorhebung im Text).
Auch in der Betriebswirtschaft, insbesondere im Bereich der Unternehmensforschung, werden Planungsprobleme untersucht. Eine allgemeine Definition aus diesem Bereich betont wiederum eher den Vorgang des Planens:
"Planung ist die gedankliche Vorwegnahme zukünftigen Handelns durch Abwägen verschiedener Handlungsalternativen und Entscheidung für den günstigsten Weg. Planung bedeutet also das Treffen von Entscheidungen, die in die Zukunft gerichtet sind und durch die der betriebliche Prozeßablauf als Ganzes und in allen seinen Teilen festgelegt wird" (Wöhe, 1981, S. 125, Hervorhebung im Text).
Andererseits kann aber das Planen mehr aufgrund der Repräsentation der Problemstellung und der formalen Darstellung der Lösungsfindung definiert werden. Diese Art der Definition ist vor allem in der künstlichen Intelligenz (KI) üblich. Wilkins, nach dem "the problem of generating a sequence of actions to accomplish a goal is referred to as planning." (Wilkins, 1984, S. 269, Hervorhebung im Text), beschreibt die klassische Art des Planens in der KI folgendermaßen:
"The classical definition of the planning problem assumes a state-based representation of the world. This means that the world is represented by taking a 'snapshot' of it at one particular time and describing the world as it appears in this snapshot... " (Wilkins, 1988, S. 4)
Planen in diesem Sinne kann als Variante des Problemlösens betrachtet werden, wenn es darum geht, eine Folge von Operationen zu finden, die zu einer günstigen Lösung führt (siehe Hacker, Heisig, Hinton, Kodwa & Wiesner, 1992).
Die meisten Modelle zum Planen wurden im Bereich der künstlichen Intelligenz (KI) entwickelt. Hertzberg (1989, S. 11) nennt neben der KI auch automatisches Programmieren, Konfigurieren, Operations Research, Betriebswirtschaft oder Sozialwissenschaften, die sich mit dem Gegenstandsbereich der Planung befassen.
Meist steht der Versuch im Vordergrund, einen "lauffähigen Planer" zu konstruieren, d.h. ein Programm, das möglichst in Echtzeit innerhalb einer gegebenen Umgebung Pläne zur Erreichung vorgegebener Ziele erstellen kann. "That is, the goal is not so much a theory of cognition but a program that performs certain tasks efficiently" (Wilensky, 1983, S. 6). Wilkins charakterisiert knapp die wesentlichen Merkmale des Planens in der KI:
"The automation of planning in a computer program involves representing the world, representing actions and their effects on the world, reasoning about the effects of sequences of such actions, reasoning about the interaction of actions that are taking place concurrently, and controlling the search so that plans can be found with reasonable efficiency" (Wilkins, 1984, S. 269).
Diese einzelnen Aktionen, aus denen sich ein Plan zusammensetzt, werden als Operatoren bezeichnet. Wilkins beschreibt Operatoren so:
"The actions that can be taken in the world must be represented in such a way that the planner can take the state of the world in which the action is performed and map it into the state of the world that will exist after the action is performed. Such a representation of an action is called an operator" (Wilkins, 1988, S. 4 f, Hervorhebung im Text).
Je nachdem, welche Algorithmen und Repräsentationen den Planungsmodellen der KI zugrunde liegen, können verschiedene Arten des Planens abgegrenzt werden:
In der KI wird die grundsätzliche Unterscheidung zwischen einstufigem Planen, wobei sich der Plan auf einer Ebene (und zwar meist auf der Ebene der ausführbaren Aktionen) bewegt, und mehrstufigem Planen, bei dem der Plan auf verschiedenen Abstraktionsebenen erstellt wird, getroffen. Beim einstufigen Planen unterscheidet man folgende Vorgehensweisen:
Planen als Deduktion: Bei den ersten Planungssystemen wurde versucht, einen Plan als einen Theorembeweis zu formalisieren. Ein Beispiel hierfür ist das Situationskalkül von McCarthy und Hayes, das in Hertzberg (1989, S. 21 - 25) dargestellt wird. Es wird versucht, aus der Startsituation unter Anwendung der Operatoren die Zielsituation zu beweisen; die einzelnen Schritte des Beweises entsprechen dann dem Plan.
Planen als Suche: Jede Situation wird dabei - im Gegensatz zur rein "logischen" Repräsentation - immer vollständig beschrieben; es sind also in jeder Situation alle Merkmale enthalten. Man kann dieses Prinzip so charakterisieren: "Wenn man beim Planen von einer Situation in eine andere gelangt, stellt man sich das so vor, daß die Beschreibung der alten Situation in die neue hinüberkopiert wird, verändert nur um die Merkmale, die der Operator verändert" (Hertzberg, 1989, S. 45). In der sogenannten Add-List wird dabei angegeben, welche Merkmale in der neuen Situation hinzukommen, in der Delete-List sind diejenigen Merkmale aufgeführt, die in der neuen Situation nicht mehr gültig sein sollen; die Preconditions geben an, welche Bedingungen zur Anwendung einer Operators erfüllt sein müssen. Es handelt sich hier um die Suche in einem Zustandsraum, der durch die Anwendung aller anwendbaren Operatoren auf die jeweiligen Situationen expandiert werden kann. Eines der ersten und das wohl bekannteste Planungssystem, das Planen als Suche in einem Zustandsraum betrachtet, ist das System STRIPS (von STanford Research Institute Problem Solver) von Fikes und Nilsson (1971).
Nichtlineares Planen: Beim nichtlinearen Planen soll vermieden werden, daß zu früh eine bestimmte Reihenfolge der Operatoranwendung festgelegt wird; die Operatoren sollen lediglich partiell geordnet werden. Beim nichtlinearen Planen sucht man nach parallelen Teilplänen, deren Abarbeitung nicht voneinander abhängt; Georgeff (1987, S. 375) spricht in diesem Zusammenhang von kommutativen Teilplänen. Sogenannte Abhängigkeiten sagen, welcher Teil eines Planes Voraussetzung für einen anderen ist.
Das mehrstufige Planen, oft auch als hierarchisches Planen bezeichnet, entspricht eher den beim Menschen stattfindenden kognitiven Vorgängen als das einstufige Planen. Eine Reduktion der Komplexität der Planungsaufgabe soll dadurch erzielt werden, daß zuerst ein grober Plan erstellt wird, der dann schrittweise verfeinert werden kann. Diese Abstraktion kann sich sowohl auf die Situationen als auch auf die verwendeten Operatoren beziehen.
Situationsabstraktion: Bei der Situationsabstraktion geht es nach Hertzberg (1989, S. 131 ff) darum, die einzelnen Merkmale einer Situation zu gewichten; den wichtigsten Merkmalen wird ein hoher Index, den weniger wichtigen ein niedrigerer Index zugeordnet. Bei der Erzeugung von abstrakteren Plänen werden dann nur die Merkmale verwendet, die mindestens eine bestimmte Wichtigkeit aufweisen. Später wird dann der Plan verfeinert, d.h. auch die Merkmale mit geringerer Wichtigkeit werden in Betracht gezogen. Dabei kann es vorkommen, daß sich beim Verfeinern herausstellt, daß der abstrakte Plan so nicht realisiert werden kann; in einer solchen Situation muß dann erst wieder ein alternativer abstrakter Plan gefunden werden (z.B. durch Backtracking).
Operatorabstraktion: Bei der Operatorabstraktion werden neue Operatoren konstruiert, die eigentlich in der Welt nicht direkt ausführbar sind. Es handelt sich dabei um das Ergebnis einer Folge von Anwendung von "Primitiv-Operatoren". Diese abstrakten Operatoren werden beim Planen genauso verwendet, wie die anderen Operatoren und unterscheiden sich von diesen nur dadurch, daß sie außer den Vorbedingungen, der Add-List und der Delete-List auch noch einen sogenannten Plot beinhalten, der angibt, durch welche Teilpläne oder ausführbare Operatoren der abstrakte Operator bei seiner Verfeinerung ersetzt werden soll.
Der erste Ansatz zum hierarchischen Planen ergab sich aus einer Erweiterung des Systems STRIPS durch Fikes, Hart und Nilsson (1972). Die Generalisierung von Plänen zu sogenannten Makro-Operatoren (MACROP's) erlaubt im Vergleich zu STRIPS eine verringerte Planungszeit und komplexere Pläne.
Sacerdoti (1974) erweiterte das Konzept der Abstraktion auf eine Hierarchie von Abstraktionsräumen: Dadurch, daß ein Plan nur dann weiter in Betracht gezogen wird, wenn ein erfolgreicher Plan auf höherer Stufe für dessen Wichtigkeit spricht, kann der Teil des Suchraumes, der tatsächlich durchsucht wird, stark begrenzt werden. Beim Planen werden nach Sacerdoti (1974) jeweils eine kritische Schwelle und ein sogenannter Skelett-Plan (eine Liste von Knoten aus dem Suchbaum in einem abstrakterem Raum) verwendet; es handelt sich also um eine Realisierung des oben kurz dargestellten Konzepts der Situationsabstraktion.
Es wurden einige weitere Verfahren zur Erstellung von Plänen entwickelt. Diese sollten vor allem die Effizienz der erstellten Pläne und deren Flexibilität steigern. Folgende "klassische" Mechanismen wurden dazu entwickelt:
Planen mit Constraints: Die klassische Darstellung des Planens mit Constraints stammt von Stefik (1981a). Constraints, die Einschränkungen der Möglichkeiten der Belegung der Planvariablen, erlauben es den "individuals (objects) that appear in a plan to be partially specified" (Georgeff, 1987, S. 378). Die errechneten Constraints werden während der Planung propagiert, d.h. aus den schon bestehenden Constraints werden neue hergeleitet. Im Zuge der Constraint satisfaction wird dann für die Variablen die Teilmenge der möglichen Belegungen gefunden, die alle bestehenden Constraints befriedigt.
Meta-Planen: Meta-Planen, das Planen des Planens, wurde wiederum von Stefik (1981b) beschrieben. In diesem Artikel geht es um "...meta-planning, which enables a planner to reason (to some degree) about its own reasoning process" (Stefik, 1981b, S. 142, Hervorhebung im Text). Das Planen selbst wird dabei als ein Problem betrachtet, für den es keinen von Anfang an festgelegten Lösungsweg gibt. Das Meta-Planen soll "herausfinden, welche (Meta-)Operatoren auf einen vorliegenden unvollständigen Plan sinnvoll als nächste anzuwenden sind" (Hertzberg, 1989, S. 180).
Verteiltes Planen verteilter Problemlösungen: Beim verteilten Planen (z.B. Georgeff, 1987) erstellen mehrere Planer zusammen einen Plan, der dann von mehreren Akteuren ausgeführt wird. Die einzelnen Planer wissen nichts von der Existenz der übrigen Planer; sie besitzen ein Modell von der Welt, das nur die Merkmale enthält, die ihre Operatoren beeinflußen. Die Kommunikation zwischen den Planern findet über ein Blackboard statt (cf. Hertzberg, 1989). Ein Blackboard ist eine Datenstruktur, die alle relevanten Elemente des modellierten Ausschnittes der "Welt" enthält und auf die von den einzelnen Planern zugegriffen werden kann, wenn diese den momentanen Zustand der Welt erfragen wollen.
Nach Wilkins (1988, S. 12) zeichnen sich klassische Planungssysteme durch folgende Merkmale aus: Domänen-Unabhängigkeit, Verwendung von Planvariablen, Möglichkeit des hierarchischen Planens und von nichtlinearen Plänen. Wilkins (1988) bemängelt an den klassischen Ansätzen zum Planen insbesondere, daß sie nicht reaktiv sind, d.h. daß die Auswahl von Aktionen Änderung der Gegebenheiten der Welt, die von außen bewirkt werden, nicht berücksichtigen kann. Im Gegensatz dazu steht das Verhalten des Menschen: "Humans often simply respond to stimuli without thinking ahead. Furthermore, a classical planner might be run over by a train while it is planning" (Wilkins, 1988, S. 6).
Es existieren auch Modelle des Planens, die zwar aus dem Bereich der KI stammen, die aber dennoch auf Prinzipien aufbauen, die möglicherweise auch menschliche Problemlöser beim Planen einsetzen. In diese Kategorie fallen die beiden im folgenden dargestellten Modelle, bei denen bereits erfolgreich ausgeführte Pläne die Grundlage der Erstellung neuer Operatorsequenzen darstellen:
Der Begriff des adaptiven Planens geht auf Alterman (1988) zurück. Grundsätzlich geht es dabei darum, in neuen Situationen auf einen bereits bekannten Plan zurückzugreifen und diesen entsprechend den Erfordernissen der neuen Situation abzuändern (zu adaptieren). Die bekannten Pläne sind als Hintergrundwissen in einem Netzwerk gespeichert. Das dazu von Alterman (1988) entwickelte System PLEXUS abstrahiert soweit, bis es auf die Abstraktionsebene gelangt, die den Zweck des Schrittes enthält, der abgeändert werden soll. Bei der Ausarbeitung eines Planes muß sich PLEXUS dann wieder von einem abstrakten Plan zu spezifischeren Beispielen bewegen, die dann auch ausgeführt werden können; dies geschieht durch Spezialisierung (specialization).
Eine weitere Möglichkeit, bereits bekannte Pläne zur Erstellung neuer Pläne zu nutzen, wird beim fallbasierten (case based) Planen angewandt (cf. Hammond, 1990): Die Entscheidungen werden von einem episodischem Gedächtnis gesteuert werden, nicht durch Inferenzregeln oder Planungsoperatoren: Der am passendsten scheinende Plan wird abgerufen und in einer "Simulation" ausgeführt. So lassen sich die Stellen finden, an denen der abgerufene Plan für die Lösung der konkret vorliegenden Aufgabe nicht geeignet ist; der Plan kann dann an diesen Stellen abgeändert werden. Dieses Modell ist aber nicht als psychologische Theorie entwickelt worden, sondern es handelt sich um ein Modell aus der KI.
1.2. Planen aus psychologischer Sicht
Zu jedem Zeitpunkt während des Planungsprozesses bieten sich dem Planer aufgrund seiner Überlegungen und Beobachtungen verschiedene Möglichkeiten (opportunities, daher die obige Bezeichnung) zur Weiterentwicklung des Planes dar. Dies führt zu folgendem, im Extremfall chaotisch erscheinenden, charakteristischen Verhalten:
"In general, the assumption that people plan opportunistically implies that interim decisions can lead to subsequent decisions at arbitrary points in the planning space. Thus, a decision at a given level of abstraction, specifying an action to be taken at a particular point in time, may influence subsequent decisions at higher or lower levels of abstraction, specifying actions to be taken at earlier or later points in time" (Hayes-Roth & Hayes-Roth, 1979, S. 276).
In einer Simulation dieser Art des Planens durch Hayes-Roth und Hayes-Roth (1979) wird das Planen durch mehrere kognitive Spezialisten bewerkstelligt. Diese Spezialisten sind als Wenn-Dann-Regeln implementiert: Sie treten beim Auftreten eines vorher spezifizierten Zustands in Aktion. Die Entscheidungen der einzelnen Spezialisten werden auf einem Blackboard vermerkt, mittels dessen die verschiedenen Spezialisten interagieren und kommunizieren können.
Bei der Planung von Produktionsprozessen in der Industrie, dem sogenannten Scheduling, steht die Frage im Vordergrund "how to reach certain production criteria in the most efficient way" (Sanderson, 1989a); es geht darum, eine Reihenfolge festzulegen, in der eine Liste von Aufträgen abgearbeitet werden soll. Erfahrene menschliche Planer erstellen dabei oft trotz der komplexen Aufgaben erstaunlich effiziente Pläne. Sanderson (1989a) stellt eine Reihe von Regeln, sogenannter scheduling rules vor, die eine mehr oder weniger günstige Reihenfolge der Aufträge erzeugen. Sie diskutiert auch den Einsatz von Hybridsystemen, in denen der menschliche Planer vom Computer unterstützt wird (z.B. durch Anzeige der sich aus der momentanen Situation ergebenden zukünftigen Situationen) und von Expertensystemen zum Scheduling. Aus einer Reihe verschiedener Feldstudien zur Vorgehensweise von menschlichen Planern beim Scheduling ergibt sich folgendes Bild von erfahrenen Planern:
"These studies give a picture of expert schedulers as people who have developed a high level of expertise based on heuristics built from experience and observation. They have a strong orientation toward future events and often use some kind of look-up table of uneven granularity to make decisions or choose actions" (Sanderson, 1989a, S. 646).
Experimentelle Untersuchungen deuten darauf hin, daß erfahrene menschliche Planer effizientere Lösungen erstellen als einfache Scheduling Rules, wobei sich die menschliche Leistung bei bestimmten Umweltbedingungen verschlechtern kann (cf. Sanderson, 1989a). Gegenüber Kombinationen von Regeln zeigt sich keine deutliche Überlegenheit der menschlichen Planer mehr.
Hacker, Heisig, Hinton, Kodwa und Wiesner (1992) konnten feststellen, daß es "im Alltag eine habituelle Tendenz zu unterschiedlich detailierter [sic!] und langfristiger Handlungsvorbereitung, kurz Planungsneigung" (S. 8), gibt; die ausgesagte Planungsneigung korreliert mit der tatsächlichen Planungszeit. Sie verweisen auf Untersuchungen, in denen gezeigt werden konnte, daß diese Planungsneigung positiv mit dem Studienerfolg der untersuchten Probanden korrelierte. Wiesner (1992) konnte zum Beispiel zeigen, daß bei einer Aufgabe vom Tower-of-Hanoi-Typ und bei Studienleistungen die Leistungsgüte höher mit der Planungsneigung korreliert als mit der Intelligenz der untersuchten Personen. Wiesner (1992) kommt zu dem Schluß, "daß ein wesentliches Merkmal von Expertentum offenbar oftmals eine hohe Planungsneigung ist" (Wiesner, 1992, S. 14). Außerdem konnten Hacker et al. (1992, S. 11) folgenden Befund erbringen:
"Die ausgesagte Planungsneigung geht inhaltlich mit einem qualitativ besonderen leistungswirksamen Vorgehen beim Vorbereiten und Ausführen der Logistik-Aufgaben einher. Dazu gehören nutzensbewertete Antizipationen, Schrittfolgeoptimierung und Schrittegruppierung."
Heisig, Ullrich, Nebe und Hacker (1992) fanden, daß Planungsverhalten und Planungsneigung teilweise vom betroffenen Lebensbereich (Beruf; häusliche und familiäre Pflichten; Freizeit) abhängt; es existieren aber auch allen Bereichen gemeinsame Faktoren wie das Zielverfolgungsverhalten.
Durch psychologische Experimente konnten zwar Details der kognitiven Funktionen beim Planen gefunden werden, aber das Experimentieren
"... has been less successful at answering important questions about the status of these facts, such as which of them are crucial to the performance of the task in question, which of them are artefacts of more fundamental processes, and which of them might just as well have been otherwise" (Wilensky, 1983, S. 2).
Hoc (1988), dessen Buch den vielversprechenden Titel "Cognitive Psychology of Planning" trägt, beschreibt vor allem die klassischen Modelle zur Informationsverarbeitung des Menschen und ihre Anwendung bei Planungsaufgaben. Er kann dagegen kaum eigenständige Forschung zum Thema Planen nennen.
Es existiert bis jetzt noch keine umfassende psychologische Theorie, die als Rahmen für die verschiedenen Befunde zum Planen verwendet werden könnte. Somit lassen sich auch kaum theoriegeleitete Vorhersagen darüber treffen, wie die Bearbeitung einer Planungsaufgabe ablaufen sollte. Insbesondere existieren keine Theorien darüber, welche Lernfortschritte bei wiederholter Bearbeitung von Planungsaufgaben vom gleichen Typ zu erwarten sind und von welchen Faktoren der Planungsaufgaben deren Schwierigkeit abhängt.
Andererseits kann man aber Planen auch als Variante des Problemlösens betrachten. Darauf weisen Hacker et al. (1992) hin: "Planendes Zielverfolgen kann eine besondere Form von Problemlösen sein, nämlich des Lösens von Transformationsproblemen. Die Anforderungsstruktur dieser Problemklasse ist im Alltag als Abfolgeplanung häufig" (Hacker et al., 1992, S. 2, Hervorhebung im Original). Pfeiffer (1991) stellt wichtige Arbeiten vor, in denen Planen als Problemlösen untersucht wurde.
Es lassen sich also, wie gerade festgestellt, kaum theoretisch begründete Vorhersagen zum Lösen von Planungsaufgaben treffen. Betrachtet man jedoch das Verhalten bei der Lösung relativ komplexer Optimierungsaufgaben, sollten sich aus der Untersuchung der dabei ablaufenden Prozesse und ihrer Beeinflußbarkeit durch Unterschiede im Material aber dennoch interessante Einblicke in die Vorgehensweise beim Planen gewinnen lassen. In der dazu durchgeführten Untersuchung, die aufgrund des Mangels an theoretischen Vorhersagen einen eher explorativen Charakter trägt, standen folgende Punkte im Mittelpunkt:
Es war insbesondere von Interesse, wie sich die konkrete Darstellung der Aufgaben auf deren Lösung auswirkt und wie diese Präsentation als Teil der mentalen Repräsentation des Problemlösers verwendet werden kann. Zu untersuchen war auch die aus der Darstellung der Aufgaben resultierende kognitive Belastung beim Lösen der Aufgaben. Hacker et al. (1992) vermuten nämlich, daß in der Kapazität des Arbeitsgedächtnisses eine Grundlage des Planens beim Menschen liegt.
Werden die verwendeten Aufgaben genauer analysiert, so zeigt sich, daß neben dem eigentlichen Planen auch eine Reihe weiterer psychologischer Einflußgrößen bei der Bearbeitung der Aufgaben eine Rolle spielen: Die Schwierigkeit, die die Encodierung der Aufgabenstellung und die Eingabe der Lösungsschritte bereiten, kann sich auf die Lösungen auswirken. Von besonderem Interesse ist auch die Untersuchung des mit zunehmender Übung bei der Lösung zu erwartenden Lernfortschritt. Neben der Verbesserung der Lösungsgeschwindigkeit un der Lösungsgüte sollte auch nach dem beim wiederholten Lösen stattfindenden Strategieerwerb und der Verbalisierbarkeit der erworbenen Strategien gefragt werden. Es sollte weiter betrachtet werden, welchen Einfluß mentale Arithmetik auf die Lösung der Aufgaben ausübt. Außerdem sollte untersucht werden, welche Faktoren der Aufgabenstellung sich auf die Lösungen auswirken und wovon die subjektive Beurteilung der Schwierigkeit der Aufgaben und der Güte der jeweiligen Lösung abhängen.
Die verwendeten Aufgaben stammen aus dem Bereich der Unternehmensforschung oder des Operations Research (OR), einem Teilgebiet der Betriebswirtschaftslehre. Ein wesentlicher Teil der in diesem Bereich entwickelten mathematischen Verfahren, die zum Beispiel in dem Lehrbuch von Zimmermann (1990) dargestellt sind, beschäftigt sich mit Optimierungsproblemen, die innerhalb eines Unternehmens auftreten können; dabei kann es sich zum Beispiel um die Optimierung der Produktionsprogrammplanung bei Kapazitätsbeschränkungen oder die Mischungsoptimierung zur Erreichung einer optimalen Mischung unter dem Gesichtspunkt der Kostenminimierung handeln. Probleme dieser Art können rechnerisch durch Verfahren zur linearen Optimierung gelöst werden. Einen Spezialfall dieser Probleme der linearen Optimierung stellen die sogenannten Transport- oder Zuordnungsprobleme dar.
Für das Experiment wurden sogenannte Aufgaben zur Transportoptimierung verwendet. Dabei geht es darum, eine Menge an vorhandenen Einheiten aus verschiedenen Ausgangsorten so zu mehreren Zielorten zu verschieben, daß dadurch möglichst minimale Gesamttransportkosten entstehen. Solche Probleme stellen sich zum Beispiel der Bundesbahn: Zimmermann (1990, S. 105 f.) stellt ein authentisches Problem vor, das sich der Bundesbahn am 7. Mai 1958 stellte: Leere Waggons standen an den Orten Oberhausen (120 Wagen), Lippstadt (60 Wagen), Dortmund (120 Wagen) und Rauxel (60 Wagen) zur Verfügung; in den Orten Oldenburg (60 Wagen), Rheine (120 Wagen), Hamburg (120 Wagen) und Hagen (60 Wagen) wurden solche in unterschiedlicher Anzahl benötigt. Bei bekannter Entfernung (in Bahnkilometern) zwischen den einzelnen Orten sollten die Waggons so verteilt werden, daß insgesamt möglichst wenige Leerwagen-Kilometer entstehen sollten. Die von der Bundesbahn damals ermittelte Lösung war nicht optimal.
Bei diesen Aufgaben handelt es sich um Planungsaufgaben, weil eine Abfolge von Schritten zur Erreichung eines Ziels (einer möglichst günstigen Lösung) erstellt werden soll. Ein einzelner Schritt besteht dabei im Transport einer bestimmten Anzahl von Einheiten von einem Ort zu einem anderen.
Im Bereich der Kognitionsforschung läßt sich dieser in dem Experiment verwendete Aufgabentyp folgendermaßen einordnen: Nach Gilhooly und Green (1989) zeichnet sich ein well-defined Problem dadurch aus, daß sowohl der Startzustand als auch der Zielzustand und alle möglichen Operatoren vollständig bekannt sind. Im vorliegenden Fall handelt es sich dagegen um ein ill-defined Problem, da der Zielzustand anfangs nicht bekannt ist (er soll ja gerade entwickelt werden).
Eine weitere von den Autoren getroffene Unterscheidung betrifft die Frage, ob gegen einen Gegner, der versucht den Problemlöser zu schlagen, gespielt wird (adversary), oder ob nicht beabsichtigt wird, den Problemlöser zu besiegen (non-adversary). Bei den vorliegenden Aufgaben muß nicht gegen einen Gegner gespielt werden.
Eine letzte von den Autoren getroffene Klassifizierung besteht darin, ob die Aufgaben in einen reichhaltigen semantischen Kontext eingebettet sind (semantically rich) oder nicht (semantically impoverished). Dabei legen sie folgende Definition zugrunde: "A problem is semantically rich for solvers who bring considerable relevant knowledge to the task." (Gilhooly & Green, 1989, S. 86) Da nicht davon auszugehen ist, daß sich die Versuchspersonen, die an dem hier beschriebenen Experiment teilnahmen, bereits vorher mit ähnlichen Aufgaben beschäftigten, handelt es sich eher um semantisch arme Aufgaben.
Funke (1991, S. 186f) nennt folgende Merkmale komplexen Problemlösens:
Insgesamt sind hier nur zwei der sechs Kriterien komplexer Probleme nach Funke (1991) erfüllt. Da jedoch die wichtigsten Kriterien, die Komplexität der Situation (es liegen sehr viele Variablen vor) und die Vernetztheit der Variablen, stark ausgeprägt sind, können diese Aufgaben durchaus als komplex eingestuft werden.
Greeno (1978) stellt ebenfalls eine mögliche Klassifikation von Problemen dar. In diesem Schema müßten die verwendeten Aufgaben der Klasse der Probleme der Struktur und Transformation (problems of structure and transformation) zugeordnet werden. Wesentliche Anforderungen bei der Lösung von Aufgaben dieser Art bestehen in der anfänglichen Konstruktion eines Problemraumes und im Verständnis der angewandten Operatoren und der Lösungen. Diese Anforderungen liegen auch bei den hier gestellten Aufgaben vor: Die Versuchsperson muß eine geeignete mentale Repräsentation der komplexen Aufgabenstellung entwickeln; sie muß die Wirkungen der Operatoranwendungen (hier: Vergabe von Einheiten), die stets mehrere Variablen betreffen, verstehen; sie sollte fähig sein, ihre Lösung zu beurteilen (ob sie noch veränderungsbedürftig ist).
Hacker et al. (1992) weisen auf die Unterscheidung zwischen regelbasiertem Planen, bei dem die Lösung mittels allgemeiner Problemlösestrategien gefunden werden, und wissensbasiertem Planen, bei dem auf bereits bekannte Pläne zurückgegriffen wird, hin. Da Aufgaben dieser Art den Versuchspersonen neu sein dürften, muß eher regelbasiertes Planen stattfinden. Diese Art des Planens ist nach Hacker et al. (1992) eher als problemlöseorientiert zu betrachten.
Für Probleme dieser Art läßt sich algorithmisch eine optimale Lösung bestimmen. Zimmermann (1990, S. 90 ff) erläutert dazu folgende Vorgehensweise: Zuerst muß eine Ausgangslösung gefunden werden, das heißt eine Lösung, die das zur Verfügung stehende Angebot so auf die Orte verteilt, an denen es benötigt wird, daß dort der jeweilige Bedarf befriedigt wird; solche Lösungen werden auch als legale Lösungen bezeichnet, da sie gegen keine der vorgegebenen Randbedingungen verstoßen dürfen. Dazu beschreibt er drei unterschiedliche Verfahren mit den dazugehörigen Algorithmen:
Ausgehend von der auf eine dieser Arten erhaltenen Ausgangslösung wird diese solange schrittweise verbessert, bis die optimale Lösung gefunden ist. Dazu werden zwei Algorithmen vorgestellt (Zimmermann, 1990, S. 96 ff):
Nachdem ich die beiden Algorithmen - so wie sie in Zimmermann (1990) dargestellt sind - implementiert hatte, mußte ich aber feststellen, daß mit keinem von beiden immer eine optimale Lösung gefunden werden kann. Bei beiden Algorithmen kann es bei der iterativen Verbesserung der gefundenen Lösung vorkommen, daß die Bestimmung der nächsten zu ändernden Verbindung in eine Endlosschleife mündet.
Da diese Algorithmen also nicht immer anwendbar sind, entschied ich mich dafür, die optimalen Lösungen zu den von mir verwendeten Aufgaben folgendermaßen zu erhalten: Ich erzeugte mit einem dazu erstellten Programm alle möglichen legalen Lösungen und stellte dabei fest, welche davon die niedrigsten Kosten verursacht. Diese Vorgehensweise ist bei relativ "kleinen" Problemen, die aus nur wenigen Ausgangs- und Zielorten bestehen und bei denen nur geringe Mengen an Einheiten transportiert werden sollen, praktikabel. Bei komplexeren Problemen steigt allerdings der Rechenaufwand exponentiell; dies ist allerdings auch bei den oben aufgeführten Algorithmen aus dem Operations Research der Fall: Bei größeren Problemen, also Problemen mit vielen Ausgangs- und Zielorten und einem hohen Angebot und Bedarf können sie nicht mehr effizient eingesetzt werden.
Das von mir gewählte Verfahren, alle möglichen Lösungen zu erzeugen, bietet neben dem sicheren Finden der optimalen Lösung zwei weitere Vorteile: Erstens kann es vorkommen (etwa in 10% der von mir untersuchten Aufgabenstellungen), daß für eine konkrete Aufgabe mehrere verschiedene optimale Lösungen existieren. Wenn nur Aufgaben verwendet werden sollen, für die genau eine optimale Lösung existiert, müssen diese identifiziert werden können. Dies ist aber mit den oben aufgeführten Algorithmen nicht möglich (und im Bereich des Operations Research sicherlich auch nicht notwendig).
Zweitens wollte ich, um die einzelnen Aufgaben untereinander besser vergleichen zu können, auch die Kosten der schlechtesten - also teuersten - Lösung kennen; diese lassen sich natürlich leicht festhalten, wenn alle möglichen Lösungen und ihre Kosten bekannt sind.
Da es möglich ist, die kostengünstigste Lösung für Aufgaben zur Transportoptimierung zu bestimmen, ist es auch möglich, die Güte der Lösung, die eine Versuchsperson erzielt, danach zu beurteilen, wie weit die Kosten ihrer Lösung von diesem Optimum entfernt liegen. Es lassen sich auch die Ergebnisse der Bearbeitung von Aufgaben vergleichen, bei denen die optimale Lösung unterschiedlich hohe Kosten verursacht: Die Distanz zum Optimum kann dazu an dem numerischen Wert des Optimums normiert werden, indem der Quotient aus der Distanz zum Optimum und den Kosten der optimalen Lösung gebildet wird. Somit erhält man ein Maß für die Güte der Lösung, das nicht von der Höhe der Kosten der Aufgabe abhängt.
Ein weiterer Vorteil von Aufgaben dieses Typs liegt darin, daß davon auszugehen ist, daß sich die Versuchspersonen nicht in ihrem Vorwissen zur Lösung solcher Probleme unterscheiden, da Personen der untersuchten Population, überwiegend Studenten der Psychologie, üblicherweise nicht mit Problemen dieser Art konfrontiert werden. Das zum Lösen der Aufgaben benötigte Vorwissen sollte eigentlich nur in allgemeinen Lösungsstrategien, der Fähigkeit zum Größenvergleich von Zahlen und - je nach angewandter Lösungsstrategie - auch Wissen zur Addition und Multiplikation bestehen. Dieses benötigte Wissen sollte bei allen Versuchspersonen vorhanden und gut geübt sein. Die weiteren zur Lösung der Aufgaben nötigen Informationen wurden den Versuchspersonen in der Instruktion vermittelt. Aufgaben dieser Art, zu deren Lösung nur das in den Instruktionen genannte Wissen notwendig ist, werden von VanLehn (1989) als knowledge-lean (wissensarm) bezeichnet.
Ein Beispiel für die verwendeten Aufgaben läßt sich in den Instruktionen für die Versuchspersonen, die in Anhang C und Anhang D zu sehen sind, finden.
2. Faktoren der Aufgabenbearbeitung
Eine Analyse der Vorgänge und Entwicklungen beim Lösen komplexer Planungsaufgaben erfordert nicht nur den Einbezug der zum Thema Planen relevanten Aspekte. Es spielen auch eine Reihe anderer Themengebiete eine Rolle: Die Qualität der Darstellung der benötigten Informationen (Ergonomie); bei Optimierungsaufgaben, ob zur Realisierung der Lösung Berechnungen notwendig sind; die Belastung des Arbeitsgedächtnisses während des Lösens der Aufgaben (work-load); der Erwerb von Lösungsstrategien und die mentale Repräsentation der Aufgabenstellung durch die Versuchsperson. Werden alle diese Faktoren berücksichtigt, kann versucht werden, eine Vorstellung davon zu entwerfen, wie die Versuchspersonen die Aufgaben gelöst haben. Im folgenden werden deshalb zuerst die Erkenntnisse zu den wesentlichen Faktoren der Aufgabenbearbeitung dargestellt werden.
Das hier beschriebene Experiment wurde am Computer durchgeführt. Weil die Informationen zur Aufgabenstellung den Versuchspersonen am Bildschirm präsentiert wurden und die Eingabe der Lösung mittels der Maus und der Tastatur erfolgte, spielt es bei der Bearbeitung der Aufgabe auch eine Rolle, wie benutzerfreundlich (ergonomisch) die Aufgabendarstellung und die Eingabemechanismen sind.
Die Entwicklung der Bildschirmgestaltung erfolgte dadurch, daß in einem Vorversuch, an dem insgesamt 20 Versuchspersonen teilnahmen, verschiedene mögliche Varianten der Präsentation getestet und evaluiert wurden. Auf diese Weise wurde versucht, die Bildschirmgestaltung iterativ zu verbessern.
Es lassen sich allgemeine Prinzipien festlegen, denen jede Darstellung von Informationen genügen sollte. Shneiderman (1987) stellt folgende Liste von Kriterien vor, die eine Bildschirmdarstellung von Daten erfüllen sollte:
Bei der Erstellung der Bildschirm-Gestaltungen für das Experiment wurde versucht, diese Kriterien möglichst zu beachten.
Wenn die Eingabemechanismen einer Schnittstelle zwischen Mensch und Maschine so gestaltet sind, daß zur Ausführung einer Aktion direkt die von der Maschine angezeigten Objekte manipuliert werden, spricht man von Direktmanipulation. Shneiderman (1987) nennt folgende Merkmale, die die Direktmanipulation kennzeichnen:
Durch die graphische Darstellung und die Direktmanipulation soll der Benutzer des Systems den Eindruck haben, direkt die relevanten Einheiten manipulieren zu können, anstatt mit einem Computer zu interagieren (cf. Norman, 1986; Hutchins, Hollan & Norman, 1986). Dadurch wird die kognitive Belastung beim Umgang mit dem System reduziert, da der Zwischenschritt der Umformulierung der Ziele in eine für das System geeignete Repräsentation entfällt.
Gerade bei der Lösung sehr komplexer Aufgaben sollte die kognitive Belastung durch das Interface möglichst gering gehalten werden. Dies wurde bei der Erstellung der Interfaces für das Experiment durch Verwirklichung der Grundsätze der Direktmanipulation versucht.
Bei der für das Experiment verwendeten Klasse von Aufgaben handelt es sich um Optimierungsaufgaben, die üblicherweise mittels algebraischer Verfahren optimal gelöst werden können. Die tatsächlich verwendeten Aufgaben waren jedoch alle so konzipiert, daß sie auch ohne Zuhilfenahme mentaler Arithmetik optimal gelöst werden konnten; es war nur erforderlich, eine Menge von Zahlen in eine Rangreihe zu bringen bzw. die Größe von Zahlen zu vergleichen. Wenn bei der Lösung der Aufgaben dennoch gerechnet wurde, müßten die für mentale Arithmetik typischen Phänomene, die im folgenden dargestellt werden, nachweisbar sein.
Dehaene (1989) zählt folgende Effekte auf, die sich durch Experimente zum Größenvergleich von Zahlen aufweisen lassen:
Diese Effekte konnten z.B. von Dehaene (1989) experimentell gezeigt werden. Es ist jedoch wichtig, zu beachten, daß die Unterschiede in den Reaktionszeiten zwar signifikant sind, es sich aber um absolut gesehen nur geringe Unterschied handelt. Die Mittelwerte der Reaktionszeiten in den Experimenten von Dehaene (1989) schwankten z.B. zwischen 375 und 620 Millisekunden.
Nach Dehaene (1989) deutet der kontinuierliche Distanz-Effekt darauf hin, daß die Zahlen analog encodiert werden. "In comparison tasks, the magnitude of numbers appears to be represented on a continuum that conserves neighbourhood relationships, a mental map called the number line" (Dehaene, 1989, S. 562; Hervorhebung im Original).
In den von Dehaene (1989) durchgeführten Experimenten zeigte sich eine Asymmetrie im Nachlassen der Reaktionszeiten bei größerer Distanz: Er verglich Zahlen, die gleich weit entfernt vom Standardwert lagen, wobei eine der Zahlen um den gleichen Betrag kleiner war als der Standardreiz, die andere um den selben Betrag größer. Bei einer gleichen numerischen Distanz zu den Extremwerten (der größten bzw. kleinsten möglichen Zahl) wird für die größere Zahl eine längere Reaktionszeit benötigt; längere Reaktionszeiten deuten wiederum auf eine größere Ähnlichkeit zwischen den verglichenen Werten hin. Dieser Befund legt nahe, daß die Zahlen intern auf einer logarithmischen Skala codiert sind.
Größenvergleich von Zahlen nach Dehaene, Dupoux und Mehler (1990)
Aufgrund der vorliegenden Befunde zum Größenvergleich von Zahlen stellten Dehaene et al. (1990) folgendes Modell auf: In einem ersten Schritt, der Encodierung, wird der digitale Kode der Zahlen auf eine interne Größe abgebildet, die auf einem analogen Zahlenstrahl liegt. Diese Stufe ist schnell und hängt nicht davon ab, um welche spezielle Zahl es sich handelt; nur Zahlen, die aus gleichen Ziffern bestehen, wie z.B. 66, benötigen eine etwas längere Zeit zur Encodierung.
Der zweite Schritt, der Vergleich selbst, findet rein analog statt, ohne daß nochmals auf die digitale Repräsentation der Zahl zurückgegriffen wird. Die für diesen Vergleich benötigte Zeit hängt von dem Abstand der zu vergleichenden Zahlen und den Endpunkten, also der größten und der kleinsten möglichen Zahl ab.
Die letzte Stufe besteht in der Auslösung einer Reaktion, wobei eine von zwei möglichen Antworten produziert wird.
Die Zeit, die benötigt wird, um eine einziffrige Addition oder Multiplikation auszuführen, hängt nach Dehaene (1992) von der Größe der Zahlen ab (problem size effect): Die Lösungszeit ist proportional zum Produkt der Operanden oder zum Quadrat ihrer Summe; eine Ausnahme bilden Operationen, bei denen beide Male die selbe Zahl verwendet wird: Hier nimmt die Lösungszeit nur geringfügig mit der Größe der Zahl zu. Der Autor empfiehlt deshalb, in diesem Zusammenhang nicht von einem Effekt der Problemgröße zu sprechen, sondern von einem Effekt der Problemschwierigkeit (problem difficulty).
Die Erklärung, daß das Ergebnis von Additionen durch Abzählen erhalten wird, und deshalb bei großen Zahlen mehr Zeit benötigt wird, wird von Ashcraft (1992) mit folgender Begründung ausgeschlossen: Bei Erwachsenen erfolgt die Reaktion zu schnell, als daß entsprechend hochgezählt werden könnte. Außerdem zitiert Ashcraft (1992) eine eigene ältere Untersuchung, in der ein exponentielles Anwachsen der Lösungszeit gefunden wurde; einfaches Abzählen läßt aber ein lineares Anwachsen erwarten.
Der Effekt der Problem-Größe läßt sich dadurch erklären, daß die Ergebnisse als Fakten in einem mentalen Netzwerk, einem Lexikon, abgespeichert sind. Die Effekte der Größe und von gleichen Zahlen hängen von der Dauer und Schwierigkeit des lexikalischen Zugriffs auf die Einheiten ab.
Der Zeitaufwand für die Berechnung von mehrstelligen Operationen setzt sich nach Dehaene (1992) aus folgenden Anteilen zusammen:
Die Addition von mehrstelligen Zahlen erfolgt spaltenweise von rechts nach links. Dies läßt sich zum Beispiel daran demonstrieren, daß bei Verifikationsaufgaben die Berechnung sofort abgebrochen wird, wenn ein Fehler auftaucht.
Auch die Untersuchung von gehirngeschädigten Patienten deutet auf die Existenz unterschiedlicher Prozesse für den Abruf arithmetischer Fakten und für ihre Aneinanderreihung hin: Patienten können oft noch einstellige Operationen durchführen, aber keine mehrstelligen.
Sokol und McCloskey (1991) gehen davon aus, daß ein System zur Verarbeitung von Zahlen aus drei Komponenten besteht muß:
Das Berechnungssystem selbst besteht wieder aus drei verschiedenen Subsystemen:
Die Evidenz für das Bestehen dieser getrennten Einheiten besteht in der Schilderung von gehirngeschädigten Personen, bei denen nur jeweils eines dieser Systeme betroffen ist (z.B. Sokol & McCloskey, 1991).
Da es sich bei den zu bearbeitenden Aufgaben um komplexe Planungsaufgaben handelte, die sich aus sehr vielen interagierenden und somit gleichzeitig zu beachtenden und zu behaltenden Variablen zusammensetzten, spielen auch die Kapazität bzw. die Grenzen der Kapazität des Arbeitsgedächtnisses bei ihrer Lösung eine wichtige Rolle. Hinweise zur Bedeutung und Messung der Work-Load werden z.B. von Wickens (1992) dargestellt.
Meshkati (1988) weist zuerst darauf hin, daß individuelle Differenzen und Persönlichkeitsmerkmale einen starken Einfluß auf die jeweilige Work-Load haben können. Er stellt dann ein multifaktorielles Modell vor, nach dem Work-Load folgende Ursachen und Auswirkungen haben kann (cf. Meshkati, 1988, S. 306ff.):
In dem genannten Artikel werden die hier aufgeführten Faktoren noch weiter untergliedert und beschrieben.
Meshkati und Loewenthal (1988) untersuchten den Zusammenhang zwischen der bei der Bearbeitung einer Aufgabe auftretenden Work-Load und der subjektiven Einschätzung der Aufgabenschwierigkeit durch die Versuchspersonen. Es zeigte sich zwar, daß insgesamt die wahrgenommene Aufgabenschwierigkeit mit der Work-Load zunahm; wie stark der Zusammenhang war, hing jedoch vom Entscheidungs-Stil der Versuchspersonen ab. Der Entscheidungs-Stil bestimmt, wie viele verschiedene Informationsquellen eine Person zur Entscheidungsfindung heranzieht und wie viele Informationen vor einer Entscheidung gesammelt werden.
Nach den Ausführungen von Anderson (1987) zum Erwerb von Programmierkenntnissen besteht eine Hauptquelle von Fehlermöglichkeiten darin, daß aus dem Arbeitsgedächtnis Elemente verloren gehen, weil zu viele Einheiten in diesem Speicher gehalten werden sollen. Dabei kann es sich um zur Lösung der Aufgabe notwendige Informationen oder Teilziele oder um den Verlust eines Merkmales, das zwischen der Anwendung verschiedener Produktionen diskriminiert, handeln. Daß die auftretenden Fehler tatsächlich auf die begrenzte Kapazität des Arbeitsgedächtnisses zurückzuführen sind, begründet der Autor folgendermaßen:
"Increasing the complexity of one part of the problem increased errors in another part, suggesting that the capacity requirements to represent one part overflowed and had an impact on the representation of another part. Further, errors were nonsystematic; that is, subjects did not repeat errors as one would expect if there were some systematic misconception" (Anderson, 1987, S. 202).
In einer Serie von Experimenten zur Vorhersage oder Verifikation des Outputs einer Verbindung von logischen Schaltzeichen zeigten Carlson, Sullivan und Schneider (1989), daß eine hohe Gedächtnisbelastung (memory set size) durch Elemente, auf die nicht zugegriffen werden muß, kaum mit den Entscheidungsaufgaben interferiert. Muß dagegen auf die Elemente zur Entscheidungsfindung zugegriffen werden, kommt es zu hohen Kosten (die sich in einer Erhöhung der Lösungszeiten um ca. 800 Millisekunden äußern), die außerdem mit zunehmender Übung nicht abnehmen. Dies begründen sie damit, daß getrennte Gedächtnissysteme zur Speicherung und zur Verarbeitung von Information verfügbar sind. In einer weitergehenden Untersuchung mit ähnlichem Aufbau kamen Carlson, Khoo, Yaure und Schneider (1990) zu folgendem Fazit:
"Tasks that demand only loading information and buffering responses ... interfered primarily early in practice. A task that required constructing and inspecting new representations ... continued to interfere substantially with problem solving after extensive practice, although the amount of interference continued to decline" (Carlson et al., 1990, S. 212).
Die Autoren ziehen daraus den Schluß "that coordinating and integrating representations is a separable component of complex skills" (Carlson et al., 1990, S. 212). Dies wäre also ein Beispiel für eines der verschiedenen Komponenten des Arbeitsgedächtnisses.
Wickens (1992) stellt die sogenannte Multiple-Resource Theorie dar, nach der "people have several different capacities with resource properties. Tasks will interfere more and difficulty-performance trade-offs will be more likely to occur, if more resources are shared" (Wickens, 1992, S. 375). Für die Bearbeitung verschiedener Aufgaben werden demnach, je nach deren Verarbeitungsstufe (Encodierung oder Reaktion), Modalität (visuell oder auditiv) und Verarbeitungskode (räumlich oder verbal), unterschiedliche Ressourcen beansprucht.
Sweller (1988) untersuchte das Verhalten beim Lösen geometrischer Aufgaben. Er stellte fest, daß Problemlösen durch Anwendung der Mittel-Ziel-Analyse zu einer hohen Belastung des Arbeitsgedächtnisses führt, da der momentane Zustand, das Ziel und der Ziel-Stack (die noch nicht vollständig abgearbeiteten Teilziele) gemerkt werden müssen. Die Gedächtnisbelastung wird dagegen geringer, wenn kein spezifisches Ziel vorgegeben wird, sondern nur die Aufforderung erfolgt, die Werte möglichst vieler Variablen zu errechnen. Unter diesen Umständen kann die Mittel-Ziel-Analyse nicht angewandt werden, da ja kein Ziel vorgegeben ist. Die Versuchspersonen müssen die Lösungen durch forward-working strategies finden. In diesem Fall ist die kognitive Belastung niedriger, wie sich durch die geringeren Fehlerquoten bei der eigentlichen Aufgabe und die geringere Beeinträchtigung einer Sekundär-Aufgabe (Memorieren der Aufgabenstellung und Lösung der vorherigen Aufgabe) zeigen ließ. Die höhere Belastung des Arbeitsgedächtnisses führt dazu, daß weniger Kapazität zum Erwerb von Schemata frei bleibt:
"A problem solver whose cognitive processing capacity is entirely devoted to goal attainment is attending to this aspect of the problem to the exclusion of those features of the problem necessary for schema acquisition" (Sweller, 1988, S. 262).
Die Verfügbarkeit von Schemata stellt nach Reimann und Chi (1989) eine Voraussetzung für das Lösen von Problemen dar. Sweller faßt die Ergebnisse folgendermaßen zusammen: "The theoretical points made in the present paper suggest that cognitive effort expended during conventional problem solving leads to the problem goal, not to learning. Goal attainment and schema acquisition may be two largely unrelated and even incompatible processes" (Sweller, 1988, S. 283).
Sweller, Chandler, Tierney und Cooper (1990) untersuchten die praktischen Implikationen der Tatsache, daß eine geringere kognitive Belastung den Schema-Erwerb, also das Lernen begünstigt. Sweller et al. (1990) konnten nachweisen, daß Instruktionsmaterial, bei dem Texte und Diagramme integriert sind, so daß keine andauernden Querverweise (die die Aufmerksamkeit vom eigentlichen Problem ablenken) notwendig sind, in bezug auf folgende abhängigen Variablen zu günstigeren Ergebnissen führen als konventionelle Texte:
Hussy (1991) variierte nicht die Belastung des Arbeitsgedächtnisses durch die zu bearbeitende Aufgabe, sondern er betrachtete die Wirkung des Personenmerkmals Verarbeitungskapazität auf den Strategieerwerb. Dazu bediente er sich des Szenarios der Schneiderwerkstatt, bei dem "über 20 System- und 10 Eingriffsvariablen, die miteinander in vielfältiger und intransparenter Weise miteinander vernetzt sind" (Hussy, 1991, S. 210), verwendet wurden. Er konnte zeigen, daß hohe Verarbeitungskapazität einer Versuchsperson zu einem besseren Erkennen von Regelhaftigkeiten und somit zu einer Entlastung des Arbeitsgedächtnisses führt, was sich in einer besseren Strategieoptimierung bemerkbar macht. Auch auf diesem Wege ließ sich also ein Zusammenhang zwischen Verarbeitungskapazität und Strategieerwerb zeigen.
Werden Probleme vom gleichen Typ wiederholt gelöst, so sollte es dazu kommen, daß der Problemlöser bestimmte Strategien entwickelt, mit denen er die entsprechenden Aufgaben einfacher lösen kann; er muß dann nicht mehr bei jeder einzelnen Aufgabe eine Lösung entwickeln, sondern kann die entwickelte Strategie direkt anwenden. Die Ausführung von Strategien bei der Bearbeitung eines Problems kann man auch als cognitive skills (kognitive Fertigkeiten) bezeichnen. Colley und Beech (1989) nennen folgende Merkmale von solchen geübten kognitiven Fertigkeiten:
Simon (1975) untersuchte den Strategieerwerb bei dem Bearbeiten des Tower-of-Hanoi-Problems. Die dabei diskutierten Strategien wurden in einem Produktionssystem implementiert. Zum Erwerb dieser Strategien durch die Versuchspersonen müssen bestimmte Konzepte verfügbar sein (z.B. Rekursion) oder gefunden werden (z.B. Subpyramiden); es müssen ganze Sequenzen von Operatoranwendungen gemerkt werden oder neue perzeptuelle Test (die die Anwendbarkeit einer Strategie überprüfen) entwickelt werden.
VanLehn (1991) identifizierte aus Verbalprotokollen, die bei der Lösung des Tower-of-Hanoi erhoben wurden, die Situationen, in denen neue Strategien erworben wurden; ein dazu entwickeltes Produktionssystem konnte 96% der Zeilen in den Protokollen erklären. Der Strategieerwerb kann durch das erfolgreiche Testen von Hypothesen ausgelöst werden. Ein möglicher anderer Auslöser besteht in einem sogenannten impasse, also einer Situation, in der der Problemlöser mit seinem verfügbaren Wissen nicht mehr weiß, welchen Schritt er als nächsten unternehmen soll. Der Moment des Erwerbes von Regeln zeigt in fast allen Fällen charakteristische Merkmale in den Verbalprotokollen: "In all but one case ... rule acquisition events were accompanied by signs of unusual cognitive activity, such as long pauses, negative comments, or reflective announcements of new insights into the puzzle's structure" (VanLehn, 1991, S. 27).
Die für das Experiment verwendeten Aufgaben gehören zu jener Klasse von Aufgaben, zu deren Lösung eine relativ einfaches Prinzip genügt. Wird ein solches Prinzip erkannt, dann sollte es auch von da an beibehalten werden. Dieses Erkennen der optimalen Lösungsstrategie würde dem entsprechen, was man in der gestaltpsychologischen Tradition als Einsicht (z.B. Dunker, 1935) bezeichnet. Auch in der neueren Kognitionspsychologie taucht dieses Konzept erneut auf: Kaplan und Simon (1990) versuchen, Einsicht als Wechsel des Problemraumes bei der Lösung einer Aufgabe zu erklären. Für eine Lösung ohne Einsicht werden dagegen innerhalb des selben Problemraumes verschiedene Strategien entwickelt und getestet. Dieser Gedankengang wird zum Beispiel auch von Anderson (1993) aufgegriffen.
Ein für das Vorgehen bei der Lösung eines Problems sehr entscheidender Einfluß geht von der Art, in der das Problem mental vom Problemlöser repräsentiert wird, aus. Dies zeigt sich besonders deutlich darin, daß eine experimentell herbeigeführte Variation der Problemrepräsentation bei sogenannten isomorphen Problemen (die auch in dem beschriebenen Experiment verwendet wurden) deutliche Unterschiede in der Aufgabenschwierigkeit bewirken kann.
Chi, Feltovich und Glaser (1981) definieren den Begriff Problemrepräsentation folgendermaßen: "A problem representation is a cognitive structure corresponding to a problem, constructed by a solver on the basis of his domain-related knowledge and its organization." (Chi, Feltovich & Glaser, 1981, S. 121f.; Hervorhebung im Original) Eine etwas spezifischere Definition lautet:
"The contents of a problem representation are quite straightforward in puzzle-type domains since the initial and final states as well as the exact operators are well defined. Thus, the representation, by definition, is the specification of these objects, operators and constraints, as well as the initial and final states" (Reimann & Chi, 1989, S. 165).
Von der Art dieser Problemrepräsentation hängt die Schwierigkeit der Lösung ab (siehe unten: isomorphe Probleme). Chi, Feltovich und Glaser (1981) fanden bei Experimenten mit Aufgaben aus der Domäne der Physik, daß Experten aufgrund von Hinweisen in den vorliegenden Daten ein Schema aktivieren und somit die Aufgaben gemäß den ihnen zugrundeliegenden physikalischen Prinzipien kategorisieren. Novizen dagegen gründen ihre Repräsentation der Aufgabe auf konkreten Merkmalen des jeweiligen Problems. Die Art der Repräsentation eines Problems hängt also auch davon ab, über welche Problemschemata oder Kategorien der Problemlöser verfügt. Reimann und Chi (1989, S. 169) "view the development of a problem representation as the successive attempts at instantiating schemata."
In dem hier beschriebenen Experiment dürfte es sich bei allen Versuchspersonen um Novizen handeln. Da alle Aufgaben vom gleichen Typ waren, sollte sich die Repräsentation während des Experiments nur aufgrund der zunehmenden Übung ändern.
Isomorphe Probleme können anhand des Graphen des ihnen zugrundeliegenden Problemraumes definiert werden: "... two problems are isomorphic if the graph of one problem can be mapped onto the graph of the other, with nodes and links corresponding one to one" (Kotovsky & Simon, 1990, S. 147).
Die Problemrepräsentation bestimmt die Schwierigkeit bei der Lösung einer Aufgabe und das Ausmaß des Transfers zu ähnlichen Aufgaben. Nach Kotovsky und Fallside (1989) wird die interne Problemrepräsentation entweder durch die externe Repräsentation wichtiger Aufgabenmerkmale oder durch die "Cover story" bestimmt. Die selben Autoren konnten auch in einer Serie von Experimenten feststellen, welche Problemrepräsentationen von bestimmten Aufgabenstellungen hervorgerufen werden, indem sie die interne Repräsentation unabhängig von der äußeren Repräsentation manipulierten.
Hayes und Simon (1977) zeigten, daß isomorphe Probleme (in dem beschriebenen Experiment handelte es sich um Varianten des Tower-of-Hanoi), also Probleme, denen der selbe Problemraum zugrunde liegt und zu deren Lösung exakt die gleichen Operatoren zur Verfügung stehen, erhebliche Unterschiede bei der Schwierigkeit ihrer Lösung bereiten können. Diese Unterschiede begründen die Autoren damit, daß sich der Problemlöser eine unterschiedliche Repräsentation des Problems bildet, aufgrund derer die Lösung gefunden werden soll.
Kotovsky und Simon (1990) fanden in einer Serie von Experimenten mit verschiedenen isomorphen Varianten des chinesischen Puzzles, daß der Hauptgrund für deren unterschiedliche Schwierigkeit darin bestand, daß es unterschiedlich schwierig zu erkennen war, wie Züge durchgeführt werden: "In these problems, the limited processing resources the subjects initially bring to the problems are consumed by the task of discovering the nature of the move, to the point where they cannot do the planning, placekeeping, or other simple processing that allow a solution to be found" (Kotovsky & Simon, 1990, S. 183). Die Schwierigkeit hing dagegen in dieser Untersuchung nicht mit dem Umfang des externen Suchraums zusammen.
Mayer (1982) präsentierte seinen Versuchspersonen die gleichen algebraischen Aufgaben entweder als Gleichung oder in einen Text gekleidet. Dadurch konnte er bei den Versuchspersonen verschiedene Lösungsstrategien induzieren und nachweisen.
Die unterschiedliche Schwierigkeit isomorpher Probleme kann mit der internen Repräsentation dieser Probleme erklärt werden, die wiederum von der äußeren Präsentation der Aufgaben bestimmt wird.
Ein naheliegender Gedanke besteht darin, daß bei der Lösung der beschriebenen Aufgaben eine mentale Repräsentation der Aufgabenstellung gebildet wird, die aus einer Art lauffähiger Simulation der Situation besteht. Diese wird als mentales Modell bezeichnet.
Norman (1983) stellt kurz die Kennzeichen mentaler Modelle dar: "In interacting with the environment, with others, and with the artefacts of technology, people form internal, mental models of themselves and of the things with which they are interacting. These models provide predictive and explanatory power for understanding the interaction" (Norman, 1983, S. 7). Der Autor stellt eine Liste von Kennzeichen mentaler Modelle auf (cf. Norman, 1983, S. 8):
Johnson-Laird (1989) stellt eine Theorie des Denkens vor, die auf der Manipulation mentaler Modelle beruht. Als mögliche Quellen mentaler Modelle kommen Beobachtungen, Erklärungen anderer Leute oder die Konstruktion aus den einzelnen Komponenten oder aus analogen Modellen in Betracht (cf. Johnson-Laird, 1989, S. 487). Hinweise zur Identifikation mentaler Modelle sind in Rouse und Morris (1986) zu finden.
Brehmer (1987) geht davon aus, daß ein Display immer nur einen Teil aller möglichen Informationen anzeigt. Der Benutzer exploriert deshalb das System, um herauszufinden, wie es arbeitet. "Thereby he builds a mental model of the system that he cannot do from the information provided by the displays only" (Brehmer, 1987, S. 112).
Der Zusammenhang zwischen Repräsentation von Wissen und mentalen Modellen kommt in folgender Textpassage gut zum Ausdruck:
"A representation is a model ... if its symbolic objects behave similarly to the objects in situations that are represented, so that operations on the objects in the model have effects like those of corresponding operations in the situations. Mental models of this kind incorporate features of the situation that can go beyond the knowledge that the individual can state in propositions or other explicit forms, and the representations of situations formed as mental models can be constrained by principles that are either known or considered as hypotheses" (Greeno, 1989b).
Greeno (1989a) betont, daß Kognition eine Beziehung zwischen einem Handelnden und einer Situation darstellt, also nicht nur im Kopf des Handelnden stattfindet; um diesen Zusammenhang auszudrücken, verwendet er den Begriff situated cognition. Diese situated cognition tritt vor allem in alltäglichen Situationen auf; das wesentliche daran ist die Betonung der "cognitive processes of interaction between cognitive agents and the situations they are acting in, rather than on manipulation of symbols" (Greeno, 1989a, S. 136). Ein Beispiel für dieses Phänomen stellen Kinder von Straßenhändlern aus der brasilianischen Stadt Recife dar, die zwar Probleme mit der Schulmathematik haben, aber bei Berechnungen im geeigneten Kontext (Markt) dennoch korrekte Ergebnisse erzielen, allerdings auf ungewöhnliche Weise (cf. Carraher, Carraher & Schliemann, 1985). Ein anderes Beispiel wird in einer Untersuchung von Beach (1988) dargestellt: Geübte Barmixer stellen die zu füllenden Gläser vor sich auf, wenn ein Getränk bestellt wird. Diese Gläser dienen dann als Hinweisreiz, welche Getränke zu mischen sind. Beispiele für situative Berechnungen werden von Lave, Murtaugh und De La Rocha (1984) genannt; diesen gemeinsam ist "a tendency for individuals to use the resources available in a situation to make inferences about quantities in the situation, often in preference to using symbolic computations that are less directly connected with the problem setting" (Greeno, 1991a, S. 264). Der Autor zieht daraus die Folgerung, daß Wissen nicht nur im Kopf der Person verankert ist, sondern auch in der Fähigkeit besteht, mit bestimmten Merkmalen der Umwelt sinnvoll zu interagieren:
"The knowing of mathematics is situated in social and intellectual communities of practice, and for their mathematical knowing to be active and useful, individuals either must learn to act and reason mathematically in the settings of their practice or they must acquire capabilities to generate mathematical meaning and solutions of problems in situations that they encounter" (Greeno, 1991b, S. 76).
Dieser Einbezug der Umgebung in die Lösungsfindung kann auch bei der Interaktion von Menschen mit Maschinen stattfinden, insbesondere bei Dialogen mit einem Computer, wenn z.B. Informationen als Diagramm dargestellt werden. Die Vorteile der Darstellung von Informationen als Diagramm werden von Larkin und Simon (1987) vor allem in effizienterer Suche und leichterem Wiedererkennen gesehen; in bezug auf perzeptuelle Folgerungen, bei denen die Lösung "gesehen" wird, scheint sich ebenfalls ein Vorteil gegenüber der Darstellung als Text zu ergeben. Folgende Begründung ist möglich: "Diagrams can be better representations not because they contain more information, but because the indexing of this information can support extremely useful and efficient computational processes" (Larkin & Simon, 1987, S. 99). Mayer und Gallini (1990) spezifizieren die Bedingungen, unter denen die Darstellung als Diagramm besonders wirkungsvoll ist:
Larkin (1989) beschreibt die Implementation eines Modells als Produktionsystem, das nach dem Prinzip des display based problem solving arbeitet. Dem liegt folgende Idee zugrunde: "When a solver looks at a display, various visible objects suggest or cue information about where they ought to be placed in order to solve the problem" (Larkin, 1989, S. 323). Die Autorin geht davon aus, daß es sich dabei um eine allgemeine Methode des Problemlösens handelt. Sie erzielt vor allem den folgenden Vorteil:
"... very little must be held in internal working memory. Many attributes of the data structure are attributes of external objects. These need not be stored internally but can be observed from the environment. Others are associated directly with an object, so that the object may well serve as a helpful cue to remembering the attribute" (Larkin, 1989, S. 331).
Simon (1978) beschreibt eine mögliche Stategie zur Bearbeitung des Tower-of-Hanoi-Problems, die sogenannte perzeptuelle Strategie, die ebenfalls darauf basiert, aus der Aufgabenstellung selbst die für die nächste Aktion nötige Information abzulesen; es müssen also weniger Informationen im Arbeitsgedächtnis gehalten werden. Simon (1975, S. 273) bezeichnet diese Vorgehensweise als stimulus driven. Diese Vorgehensweise bietet wiederum vor allem den Vorteil, daß nicht so viele Einheiten im Arbeitsgedächtnis gehalten werden müssen.
Da den Versuchspersonen während des Experiments mehrere (insgesamt 21) Aufgaben des verwendeten Typs zur Bearbeitung präsentiert wurden, ist anzunehmen, daß sich ein Lernfortschritt bei der Bearbeitung der Aufgaben zeigen sollte, der vor allem die Lösungszeiten betreffen sollte.
Berry und Broadbent (1988) unterscheiden selektives und unselektives Lernen. Beim unselektiven Lernen werden die wechselseitigen Abhängigkeiten zwischen den vorkommenden Variablen gespeichert; "ultimately after much experience, the person will retain a large number of condition-action links that will secure effective performance" (Berry & Broadbent, 1988, S. 253). Eine derartige Vielzahl von Verbindungen führt dazu, daß diese nicht berichtet werden und daß ihnen eventuell wenig Vertrauen geschenkt wird. Deshalb können nur wenige genaue Verbalisierungen hervorgebracht werden. Das Lernen nach diesem auch U-mode genannten Prinzip findet außerhalb des Arbeitsgedächtnisses statt; es entspricht einem ungerichteten explorativen Verhalten des Problemlösers.
Beim selektiven Lernen dagegen werden nur wenige Variablen und die wechselseitigen Abhängigkeiten zwischen diesen beobachtet. Werden die richtigen Variablen beachtet, können dann auch die zugrundeliegenden Regeln verbalisiert werden. Das Lernen nach dem kurz S-mode genannten Prinzip findet im Arbeitsgedächtnis statt und es ist bewußt.
Nach Berry und Broadbent (1988) ist eine saliente Beziehung zwischen Eingabe und den beobachtbaren Resultaten dieser Voraussetzung dafür, daß selektives Lernen stattfindet, d.h. daß der Lernende seine Vorgehensweise bei der Lösung der Aufgabe verbalisieren kann. Folgende Faktoren beeinflußen die Salienz der Beziehung (cf. Berry & Broadbent, 1988):
Lernen im S-Modus wird unter anderem auch dadurch induziert, daß die Versuchsperson während des Lernens ihre mentalen Tätigkeiten verbalisiert. Deshalb sollte ein Kommando-Interface Lernen im S-Modus bewirken, während eine graphische direktmanipulative Oberfläche eher Lernen im U-Modus hervorrufen sollte (cf. Svendsen, 1991). Diese Hypothesen konnten experimentell bestätigt werden. Folgende überraschende Folgerung kann aus diesem Befund gezogen werden:
"The results indicate that direct manipulation may hinder effective problem solving in tasks with the same complexity and saliency as a tower of Hanoi puzzle. Hinder, not in the sense that the interface is not user friendly, but to the contrary. The interface is so supportive of thoughtless action that the user neglects to look for rules where these are called for. Thus, the experiments indicate a discrepancy between user friendliness and the usefulness of direct manipulation interfaces" (Svendsen, 1991, S. 395).
Rasmussen (1986, S. 100ff.) teilt die Kontrolle über das ausgeführte Verhalten in drei Ebenen ein: skill-based, rule-based und knowledge-based behavior. "Skill-based behavior represents sensorimotor performance during acts or activities that, after a statement of an intention, take place without conscious control as smooth, automated and highly integrated patterns of behavior" (Rasmussen, 1986, S. 100; Hervorhebung im Original). Rule-based behavior dagegen wird durch gespeicherte Regeln und Prozeduren, die im vorausgegangenen Umgang mit ähnlichen Aufgaben erworben wurden, bewußt gesteuert. Knowledge-based behavior besteht in der Entwicklung eines Planes, der auf einer Analyse der Aufgabe und der Bedürfnisse der Person beruht, zur Erreichung eines Ziels. Die interne Struktur des Systems wird dabei als mentales Modell repräsentiert.
Die von J. R. Anderson entwickelte Theorie zum Erwerb kognitiver Fertigkeiten -ACT bzw. deren Erweiterung ACT*- soll im folgenden dargestellt werden, da sie einen Rahmen für die Interpretation der experimentellen Befunde bieten kann.
Grundsätzlich geschieht der Wissenserwerb nach Anderson in drei Stufen (siehe z.B. Neves & Anderson, 1981): Zuerst werden die benötigten Fakten durch die Encodierung (Encoding) ins Gedächtnis gebracht; dann werden sie durch die Prozeduralisierung in Prozeduren umgewandelt; schließlich werden diese Prozeduren durch die Composition effizienter (schneller) gemacht.
Bei der ersten Stufe, der Encodierung (encoding), wird das aufgenommene Wissen repräsentiert. Dies geschieht zuerst deklarativ, als Menge von Fakten in einem Netzwerk von Propositionen. Diese Fakten können dadurch verarbeitet werden, daß allgemeine, domänenunabhängige Prozeduren auf sie angewandt werden. Somit können sie flexibel unter bewußter Kontrolle Schritt für Schritt abgearbeitet werden. Die Fakten werden entweder aus dem Langzeitgedächtnis abgerufen oder sie werden aus der Problemstellung abgelesen (cf. Anderson, 1993,S. 41).
Die andere Möglichkeit der Repräsentation von Wissen besteht in einem Format, das direkt, ohne Interpretationsphase, angewandt werden kann, den Produktionen; diese Form des Wissens wird als prozedurales Wissen bezeichnet. "Control over cognition and behavior lies directly in the productions. Facts are used by the productions" (Anderson, 1982, S. 374). Die Produktionen sind Regeln mit einem Wenn-Teil, der die Anwendbarkeits-Bedingungen spezifiziert, und einem Dann-Teil, der festlegt, welche Aktionen erfolgen sollen; sie arbeiten auf den Fakten in der deklarativen Datenbasis. Welche Konzepte gerade im Arbeitsgedächtnis aktiv sind bestimmt, von welchen Produktionen überprüft wird, ob sie zur Anwendung kommen sollen. "In this way ACT can focus its attention on just the subset of productions that may be potentially relevant. Only if a production is selected is a test made to see if its condition is satisfied" (Anderson, 1982, S. 373). Produktionen können auch (lokale) Variablen enthalten.
Anderson nennt den Übergang vom deklarativen zum prozeduralen Wissen Compilierung. Die zur Abarbeitung einer solchen Prozedur benötigte Zeit hängt von der Anzahl der darin enthaltenen Produktionen ab. Durch die Prozeduralisierung müssen weniger Fakten aus dem Langzeitgedächtnis ins Arbeitsgedächtnis gebracht werden, da diese direkt in den Produktionen enthalten sind:
"Every time a production matches some long-term memory network structure that has to be retrieved into working memory, the proceduralization mechanism creates a new production that has that network structure incorporated into it and that avoids the need for the long-term memory retrieval" (Neves & Anderson, 1981).
Durch die Prozeduralisierung wird also die Belastung des Arbeitsgedächtnisses reduziert.
Der Mechanismus der Composition vereint mehrere Produktionen, die hintereinander ausgeführt werden, zu einer einzigen. Im Wenn-Teil der neuen Produktion befinden sich die Wenn-Teile aller darin enthaltenen Produktionen außer denen, die aus dem Dann-Teil früherer Produktionen resultieren. Im Dann-Teil tauchen die Aktionen aller darin enthaltenen Produktionen mit Ausnahme der temporären Ziele auf.
Der Größe von durch Composition entstehenden Produktionen sind durch die Kapazität des Arbeitsgedächtnisses Grenzen gesetzt (cf. Anderson, Greeno, Kline & Neves, 1981; Anderson, 1982), da nur eine begrenzte Anzahl von Informationen aus dem Arbeitsgedächtnis abgerufen und aktiv gehalten werden kann. "If a composed production is created with a condition too large to be matched by working memory, that production will never apply and so will not be able to enter into further compositions" (Anderson, 1982, S. 384). Der Verlust von Elementen aus dem Arbeitsgedächtnis kann zu Fehlern bei der Abarbeitung der Produktion, sogenannten slips, führen (cf. Anderson, 1987). Durch Prozeduralisierung kann jedoch die Gedächtnisbelastung vermindert werden.
Composition kann dazu führen, daß selten zur Anwendung kommende Regeln, die bestimmte Ausnahmefälle betreffen, gar nicht mehr zur Anwendung kommen; so entsteht der Einstellungs-Effekt.
Anderson et al. (1981) beschreiben auch noch Mechanismen zur Wissenoptimierung, durch die die Auswahl derjenigen Methode, mit der eine Aufgabe bearbeitet werden soll, verbessert werden kann: Durch Generalisierung wird versucht, das zu erfassen, was zwei Probleme und ihre Lösung gemeinsam haben. Diskrimination, die durch eine zusätzliche Wenn-Abfrage erzielt werden kann, vermeidet, daß Operatoren zu allgemein sind und in unpassenden Situationen angewandt werden. Dies geschieht dadurch, daß die Werte der einzelnen Variablen bei korrekter und bei fehlerhafter Anwendung verglichen werden. Diskrimination und Generalisierung laufen nach Anderson (1987) automatisch und ohne bewußte Kontrolle ab. Anderson (1987) stellt im Rahmen des ACT*-Modells noch das Konzept der Strength vor: Die Stärke einer Produktion bestimmt, wie schnell diese zur Anwendung gelangt (feuert); sie ergibt sich aus der Häufigkeit der erfolgreichen Anwendung der Produktion. Durch diesen Mechanismus können vor allem auch fehlerhafte Produktionen eliminiert werden.
Anderson (1987) weist darauf hin, daß bei der Lösung eines neuen Problems zuerst sogenannte weak methods zur Anwendung kommen, wie z.B. Analogieschlüsse, Means-End-Analyse, Rückwärts-Verkettung, Hill-Climbing oder reine Vorwärts-Suche. Diese allgemeinen Methoden sind wiederum als Produktionen implementiert.
"The important feature of weak-method production rules, such as the hill-climbing production, is that they are cast in a way that makes no specific reference to any particular domain. As long as the knowledge about that domain is appropriately encoded in declarative memory, these productions can apply" (Anderson, 1987, S. 196).
Anderson (1990) geht davon aus, daß sich das Problemlösen, das in diesem Zusammenhang als "deciding what action to take" (Anderson, 1990, S. 192) definiert wird, durch eine rationale Analyse beschrieben werden kann. Bei der Suche nach dem nächsten Schritt der Lösung findet eine sogenannte iterative Plan-and-Act Structure Anwendung: Da die einzelnen Schritte nicht deterministisch zu einem bestimmten Resultat führen und da aufgrund von Gedächtnisbeschränkungen nur eine begrenzte Anzahl von Schritten im Gedächtnis gehalten werden kann, werden immer nur wenige Schritte geplant und dann ausgeführt. Dies zeigt sich nach Anderson (1990) auch bei der Beobachtung von Versuchspersonen, die das Verschiebepuzzle bearbeiten: Auf eine längere Pause (in der geplant wird) folgen immer mehrere Züge, bevor die nächste Pause eintritt. Daraus läßt sich folgende Folgerung ziehen:
"One of the interesting consequences of this iterative plan-and-act structure is that, when faced with complex problems, it inevitable forces search to take place externally, in that we choose a short sequence of steps, execute it, see the results, and choose another. Thus, in games like the eight puzzle, the search is external, in the puzzle, not internal in a mental representation of the 'problem space'. A consequence of the external nature of search is that search must take place in a forward direction" (Anderson, 1990, S. 203).
Das auf der rationalen Analyse basierende Modell von Anderson wurde auch mathematisch formuliert (siehe Anderson, 1990).
Durch die beschriebenen Mechanismen kommt es zu einer Steigerung der Geschwindigkeit bei der Ausführung der Problemlösung. Neves und Anderson (1981) stellen dazu folgende Überlegungen an: Da zu jedem Zeitpunkt die gerade ausgeführte Produktion mit der zuvor ausgeführten Produktion kombiniert werden kann, wäre ein exponentieller Geschwindigkeitszuwachs zu erwarten. Empirisch aber folgt der Verlauf der Lösungszeiten mit zunehmender Übung eher einem power-law. Die Summe mehrerer exponentiell verlaufenden Kurven ist approximativ gemäß dem power-law verteilt (cf. Lewis, 1979; dargestellt in Neves & Anderson, 1981). Da die Bearbeitung einer Aufgabe jedoch meist aus mehreren Komponenten besteht, ist also auch bei einem exponentiellen Lernverlauf der einzelnen Komponenten insgesamt ein Verlauf gemäß dem power-law zu erwarten. Außerdem führen Neves und Anderson (1981) noch an, daß kombinierte Produktionen umfangreichere Wenn-Teile haben und somit zu deren Anwendung mehr Zeit benötigt wird. Verzerrungen der Lösungszeiten können auch durch Strategiewechsel bewirkt werden, denn in diesem Fall müssen die neu verwendeten Produktionen erst wieder den oben beschriebenen Lernmechanismen unterworfen werden. Ein letzter Punkt, dessen Beschreibung auf Newell und Rosenbloom (1981) zurückgeht, besteht darin, daß die Problemstellung selbst einer gewissen Variabilität unterworfen ist. Dadurch werden gleiche längere Subsequenzen von Operatoranwendungen eher selten auftreten; deshalb wird es länger dauern, bis so viel Wissens-Composition stattgefunden hat, daß alle längeren Sequenzen berücksichtigt sind. Auch dadurch wird somit ein langsamerer als der exponentielle Lernverlauf vorhergesagt.
Die Aufgaben vom dargestellten Typ sollten von den Versuchspersonen am Computer abgearbeitet werden. Deshalb muß der benutzergerechten (ergonomischen) Darstellung der Information am Bildschirm, zu deren Erfüllung von Shneiderman (1987) eine Reihe von Kriterien genannt wurden, eine wichtige Rolle bei der Aufgabenbearbeitung beigemessen werden. Als günstig erweist sich in dieser Hinsicht die Verwendung einer direkt-manipulativen Schnittstelle.
Da das Ziel der gestellten Aufgaben eine möglichst günstige Lösung ist, können auch die bei der mentalen Arithmetik ablaufenden Prozesse einen Einfluß auf die Aufgabenbearbeitung haben. Deshalb wurden verschiedene Modelle der mentalen Arithmetik vorgestellt, die die einzelnen Komponenten der für die Ausführung von mentalen Berechnungen benötigten Zeit beschreiben.
Bei den Aufgaben spielen des weiteren die bei ihrer Bearbeitung auftretende Work-Load und die daraus resultierenden Fehlermöglichkeiten und die potentielle Behinderung des Strategieerwerbs eine Rolle. Der Strategieerwerb, der bei der wiederholten Abarbeitung von Aufgaben gleichen Typs zu erwarten ist, kann zum Beispiel durch sog. Einsicht in den Lösungsmechanismus erfolgen.
Einen wichtigen Faktor für die Lösung von Aufgaben stellt auch deren mentale Repräsentation dar. Sogenannte isomorphe Probleme können sich in ihrer mentalen Repräsentation - und deshalb auch in der Schwierigkeit ihrer Lösung - unterscheiden, obwohl sich der ihnen zugrundeliegende Problemraum formal nicht unterscheidet. Wichtige dargestellte Formen der Repräsentation bilden mentale Modelle und die Zuhilfenahme der Präsentation der Aufgabenstellung als Erweiterung des Arbeitsgedächtnisses.
Werden Aufgaben wiederholt gelöst, so zeigt sich ein Erlernen der Lösungen. Dabei wird unterschieden zwischen bewußtem, verbalisierbaren und eher unbewußten Lernen, dessen Resultate nur schwer in Worte gefaßt werden kann. Anderson entwickelte eine umfassende Theorie zur Erklärung der Lernfortschritte, die im Wesentlichen auf den Stufen Encodierung, Prozeduralisierung und Compilierung und Wissensoptimierung besteht.
3. Methode
Aus der Klasse der bereits beschriebenen Aufgaben zur Transportoptimierung wurden solche Aufgaben ausgewählt, die bestimmte, unten dargestellte Kriterien erfüllen. Die Struktur der Aufgaben, mögliche Lösungsheuristiken und die Präsentation der Aufgaben am Bildschirm sind die für das Experiment entscheidenden Charakteristika dieser Aufgaben.
Der Problemraum
Zu den oben beschriebenen Aufgaben läßt sich leicht ein Problemraum konstruieren, der aus allen möglichen "legalen Zuständen" besteht, die bei der Bearbeitung der Aufgaben auftreten können. Als legalen Zustand kann man jede auf dem Weg zu einer Lösung entstehende, eventuell noch unvollständige Lösung bezeichnen. Nicht legale Zustände, die die bestehenden Constraints bezüglich verfügbarem Angebot oder benötigtem Bedarf in einem Ort verletzen, können aufgrund der verwendeten Eingabemechanismen nicht auftreten. Eine Teilmenge des Problemraums bildet der Lösungsraum, der aus den gültigen Lösungen besteht; eine gültige Lösung zeichnet sich dadurch aus, daß das gesamte Angebot so verteilt wird, daß der gesamte Bedarf befriedigt wird.
Die verschiedenen Aufgaben unterscheiden sich in der Größe des ihnen zugrundeliegenden Problemraums, d.h. in der Anzahl der legalen Zustände, die im Laufe der Lösungssuche auftreten können. Diese Größe des Problemraums hängt von drei Faktoren ab:
Erstens spielt die Summe des Angebotes/Bedarfes eine Rolle: Die Größe des Problemraums (und auch des Lösungsraums) nimmt mit der Höhe des Gesamtangebotes bzw. des Gesamtbedarfs exponentiell zu.
Zweitens hängt die Größe des Problemraums auch von der Anzahl der Ausgangsorte und der Anzahl der Bedarfsorte ab: auch hier nimmt der Umfang des Problems mit der jeweiligen Anzahl exponentiell zu. Dieser Aspekt der Aufgaben wurde aber in dem hier zu beschreibenden Experiment nicht variiert: Es lagen jeweils genau drei Ausgangsorte und genau drei Zielorte vor, da der Vorversuch zeigte, daß diesbezügliche Variationen in den realisierbaren Grenzen keinen systematischen Einfluß auf Lösungsgüte bewirken: Im Vorversuch zeigte sich kein klarer Effekt auf die Lösungsgüte aufgrund der Variation der Anzahl der Ausgangs- oder Zielorte im Bereich zwischen zwei und vier Orten.
Drittens kann der Umfang des Problemraums auch bei einem festen Gesamtangebot und -Bedarf und bei fester Anzahl an Ausgangsorten und Zielorten noch etwa um den Faktor drei variieren: Erfolgt die Verteilung des Gesamtangebotes auf die einzelnen Ausgangsorte etwa gleich (stehen in jedem Ort also etwa gleich viele Einheiten zur Verfügung), wird der Umfang des Problemraums maximal; befinden sich dagegen an einigen Ausgangsorten nur sehr wenige Einheiten, wird er wesentlich kleiner. Analoges gilt für die Verteilung des Gesamtbedarfes auf die einzelnen Zielorte.
Die Höhe der Kosten der einzelnen Verbindungen hat keinen Einfluß auf den Umfang oder Struktur des Problemraums oder des Lösungsraumes; sie wirkt sich nur die Höhe der Kosten einer möglichen Lösung aus.
Die Mindestzahl der Schritte
Für das Experiment wurden, wie bereits oben erwähnt, nur Aufgaben verwendet, für die es nur eine einzige optimale Lösung gibt. Diese Lösung kann (auch bei gleicher Anzahl an Ausgangs- und Bedarfsorten) eine unterschiedliche Anzahl an Verbindungen enthalten, auf denen Einheiten transportiert werden müssen. Durch die Anzahl dieser Verbindungen ist gleichzeitig auch die Mindestzahl an Schritten festgelegt, die die Versuchsperson zur Lösung der jeweiligen Aufgabe ausführen muß.
Eine Lösungsheuristik
Mit der im folgenden beschriebenen, relativ einfachen Heuristik lassen sich etwa die Hälfte aller Aufgaben vom beschriebenen Typ optimal lösen; bei den restlichen Aufgaben liefert diese Heuristik immer noch Lösungen, die der optimalen relativ nahe kommen: Auf der jeweils billigsten Verbindung, auf der noch Angebot und Bedarf bestehen, werden immer möglichst viele Einheiten vergeben. Formaler kann diese Lösungsstrategie folgendermaßen beschrieben werden:
Diese Heuristik entspricht dem von Zimmermann (1990, S. 94) dargestellten Bewertungsverfahren zur Erzeugung einer Ausgangslösung. In dem Experiment wurden nur solche Aufgaben verwendet, bei denen die hier dargestellte Heuristik zur optimalen Lösung führt. Diese Klasse von Aufgaben unterscheidet sich außer in der Optimalität der Lösung nach der geschilderten Heuristik in keinem mir bekannten Aspekt von den auf diese Weise nicht optimal lösbaren Aufgaben.
Den Versuchspersonen wurde die Aufgabenstellung auf die folgende Art beschrieben (siehe auch Anhang C und D): In drei Orten, die als die Ausgangsorte A1, A2 und A3 bezeichnet wurden, befinden sich mehrere leere Eisenbahnwaggons, die zu transportieren sind. Die Anzahl der Waggons ist dabei in den einzelnen Ausgangsorten meist unterschiedlich. Analog dazu existieren genau drei Zielorte, die als B1, B2 und B3 bezeichnet wurden. An diesen wird eine unterschiedliche Anzahl an Einheiten benötigt. Bei den von mir verwendeten Aufgaben waren insgesamt immer genau so viele Waggons in den Ausgangsorten, wie in den Zielorten zusammen benötigt wurden, es blieben also keine Waggons übrig. Die Entfernungen zwischen den einzelnen Ausgangsorten und den einzelnen Zielorten waren unterschiedlich und wurden für jede einzelne Verbindung getrennt angegeben. Die Entfernungen zwischen den drei Ausgangsorten und den drei Zielorten können in einer Kostenmatrix repräsentiert werden.
Als Lösung einer Versuchsperson betrachtete ich die vollständige Angabe der zu transportierenden Einheiten für jede einzelne Verbindung, wobei die einzelnen Zahlen so gewählt werden mußten, daß der jeweilige Bedarf in den Zielorten erfüllt wurde. Die Aufgaben wurden dabei so konstruiert, daß es genau eine Lösung gibt, die am billigsten ist (siehe oben).
Es ging nun für die Versuchspersonen zuerst einmal darum, die Einheiten von den Ausgangsorten so auf die Zielorte zu verteilen, daß dort der gesamte Bedarf befriedigt wird; solange dies nicht der Fall war, wurde die Lösung nicht als fertig akzeptiert.
Die eigentliche Zielsetzung und Schwierigkeit bestand nun darin, daß der Transport von einem bestimmten Ausgangsort zu einem bestimmten Zielort mit unterschiedlichen Kosten verbunden ist, die sich bei den von mir verwendeten Aufgaben aus unterschiedlichen Entfernungen zwischen den verschiedenen Orten ergaben. Die Versuchspersonen sollten nun versuchen, die Waggons so zu verteilen, daß die Gesamtkosten der Lösung möglichst niedrig gehalten wurden. Die Gesamtkosten berechnen sich als Summe der entstandenen Kosten der einzelnen Verbindungen zwischen allen Ausgangsorten und allen Zielorten: Die entstandenen Kosten einer jeden Verbindung lassen sich aus dem Produkt der Kosten dieser Verbindung (also der Entfernung zwischen den beiden Orten) und der Anzahl der jeweils transportierten Einheiten ermitteln. Diese Kosten sollten also minimiert werden.
Die Versuchspersonen erstellten ihre Lösungen, indem sie für jede Verbindung zwischen den Ausgangsorten und den Zielorten einen bestimmten Wert eingeben konnten, der festlegte, wie viele Waggons auf dieser Verbindung transportiert werden sollen. Diese Werte konnten beliebig oft geändert werden. Es kam vor, daß Versuchspersonen für bestimmte Verbindungen zu hohe Werte eingaben, was zu einem nicht legalen Zustand geführt hätte; dies war der Fall, wenn mehr Einheiten von einem Ausgangsort wegtransportiert werden sollten, als dort noch zur Verfügung standen oder wenn an einem Bedarfsort mehr Einheiten angeliefert werden sollten, als dort noch benötigt wurden. In diesem Fall wurde dieser Wert automatisch auf den maximal möglichen herabgesetzt und sowohl der eingegebene als auch der verwendete Wert wurden mitprotokolliert. Das automatische Herabsetzen hat den Nachteil, daß Korrekturen der Werte für die Waggons nach oben (wenn ein Wert einer zulässigen Lösung erhöht werden soll) nicht sofort eingegeben werden können; stattdessen ist es erforderlich, zuerst an anderen Stellen verminderte Werte einzugeben, um an der gewünschten Stelle mehr Angebot/Bedarf zu erhalten. Dies führte bei zwei Versuchspersonen zur Bitte um Hilfestellung durch den während des Experiments anwesenden Versuchsleiter. Das automatische Herabsetzen wurde aber dennoch beibehalten, da es sonst zu negativen Werten beim verbleibenden Angebot/Bedarf hätte kommen können, wenn die Versuchsperson mehr Einheiten von einem Ausgangsort wegtransportieren wollte, als dort verfügbar waren (negatives Angebot), oder wenn sie mehr an einem Zielort anliefern wollte, als dort benötigt wurde (negativer Bedarf). Solche negativen Werte führten bei den Versuchspersonen zu großer Verwirrung, wie sich im Vorversuch herausstellte.
Die Experimente wurden an einem Personalcomputer mit VGA-Karte und Farbbildschirm durchgeführt. Die wesentliche Variation der Aufgabenstellung, die als between-subject Faktor in dem Experiment realisiert wurde, betraf die Darstellung der jeweiligen Aufgabe am Bildschirm und die Art der Eingabemechanismen für die Versuchsperson. Eine Bedingung sollte eine eher analoge mentale Repräsentation der Aufgabe bewirken, die andere Bedingung sollte eine eher digitale Repräsentation der numerischen Werte (Kosten, Angebot, Bedarf) begünstigen. Die Bildschirmdarstellung und die Protokollierung der Aktionen der Versuchspersonen wurden in Smalltalk/V unter Verwendung des Tools Widgets (zur Erstellung graphischer Benutzeroberflächen) implementiert. Die beiden realisierten Bedingungen werden nun genauer dargestellt:
Die Matrix-Bedingung
Ein Beispiel dafür, wie der Bildschirm bei der Präsentation der Aufgaben in der Matrix-Bedingung aussieht, ist in Anhang B zu sehen. Das Hauptmerkmal der Matrix-Bedingung besteht darin, daß die Kosten der einzelnen Verbindungen zwischen den Orten in Form einer Matrix dargestellt werden: Die Zeilen der Matrix entsprechen je einem Ausgangsort und sind links mit dessen Namen (z.B. "A1") beschriftet; die Spalten beziehen sich auf je einem Zielort, dessen Name (z.B. "B1") darunter angezeigt wird. Der Verbindung vom Ausgangsort A[i] zum Zielort B[j] entspricht dann die Zelle der Matrix in der i-ten Zeile und der j-ten Spalte. Jede Zelle enthält dabei folgende Informationen:
Diese Matrix wird links oben am Bildschirm dargestellt. Rechts davon wird in einer Spalte die Information zum verfügbaren Angebot dargestellt: In je einer Zeile steht für jeden Ausgangsort, wie viele Waggons von den insgesamt zur Verfügung stehenden bereits vergeben wurden (z.B. "Angebot A1: 3 v 8"). Darunter wird, durch eine Leerzeile optisch abgetrennt, auf ähnliche Weise der Bedarf dargestellt: Für jeden Zielort ist sichtbar, wie viele der benötigten Einheiten schon vorhanden sind (z.B. "Bedarf B2: 4 von 7").
Klickt die Versuchsperson mit der Maus auf eine Zelle der Matrix, öffnet sich ein Dialogfenster, in dem sie einen neuen numerischen Wert für die Anzahl der auf dieser Route zu vergebenden Einheiten eingeben kann. Handelt es sich zum Beispiel um die Zelle, die die Verbindung von dem Ausgangsort A1 zu dem Zielort B1 repräsentiert, ist in diesem Dialogfenster die Frage "Neuer Wert von A2 nach B1" zu lesen. Die Versuchsperson kann daraufhin einen Wert eingeben. Dieser Wert wird übernommen und das Dialogfenster verschwindet dann, wenn entweder auf einen Schalter in dem Dialogfenster mit der Aufschrift "ok" geklickt wird oder wenn die Eingabetaste betätigt wird; vorher kann der Wert durch die Backspace-Taste gelöscht und geändert werden. Bei dem eingegebenen Wert wird zunächst geprüft, ob es sich um eine natürliche Zahl handelt. Ist dies nicht der Fall, wird an dessen Stelle der Wert Null eingesetzt. Dann wird die Zahl auf ihre Plausibilität hin geprüft: ist sie größer als die Zahl der maximal benötigten oder vorhandenen Einheiten, wird sie automatisch auf den maximal möglichen Wert herabgesetzt. Auf diese Weise wird verhindert, daß negative Werte bei dem Rest-Angebot oder -Bedarf angezeigt werden (was, wie sich im Vorversuch herausstellte, zu Verwirrung führte). Die eingegebenen Werte können beliebig oft abgeändert werden.
Sind alle Werte eingegeben und will sie die Versuchsperson nicht mehr ändern, kann sie einen Schalter mit der Aufschrift "fertig" betätigen; daraufhin wird die gesamte eingegebene Lösung auf ihre Gültigkeit hin überprüft, das heißt daraufhin, ob das gesamte Angebot vergeben wurde und der gesamte Bedarf befriedigt wurde. Ist dies der Fall, so ist die eigentliche Bearbeitung der Aufgabe beendet; ist die Lösung ungültig, erscheint folgende Meldung: "Dieser Loesungsvorschlag erfüllt nicht die obigen Randbedingungen! (Angebot bzw. Bedarf)". Nachdem die Versuchsperson diese Meldung weggeklickt hat, kann sie die ungültige Lösung so verändern, daß sie akzeptiert wird.
Die graphische Bedingung
Ein Beispiel für die Bildschirmgestaltung der graphischen Bedingung ist in Anhang A dargestellt: Links oben am Bildschirm befindet sich ein umrahmtes Feld, das mit "Angebot (Ausgangsorte)" beschriftet ist, innerhalb dessen das Angebot für die einzelnen Ausgangsorte angezeigt wird. Das Angebot für jeden einzelnen Ausgangsort wird durch je einem Balken (BarGauge) dargestellt: Ein liegendes Rechteck steht für das gesamte Angebot; ein Teil der Fläche des Rechtecks ist dunkel eingefärbt, entsprechend dem Anteil der noch zu vergebenden Einheiten am Gesamtangebot. Rechts von dem Balken wird die graphisch dargestellte Information noch durch die explizite Nennung der entsprechenden numerischen Werte ergänzt (z.B. "3von7"), da die analoge Darstellung zur Einstellung ganz bestimmter intendierter Konfigurationen eventuell zu ungenau sein könnte. Um diesen Balken und die Anzeige des numerischen Wertes herum ist jeweils ein Rahmen gezogen, der entsprechend dem Ausgangsort beschriftet ist, z.B. mit "Angebot 1:".
Der Bedarf in den Zielorten wird auf die gleiche Weise durch BarGauges in einem darunterliegenden umrahmten Bereich dargestellt, der mit "Bedarf (Zielorte)" beschriftet ist. Die Bezeichnung der umrahmten Felder für jeden Zielort wird ebenfalls entsprechend den Orten vergeben, z.B. "Bedarf 1:". Der dunkel eingefärbte Teil des Balkens stellt wiederum dar, wie viel Bedarf von dem Gesamtbedarf an diesem Ort noch benötigt wird; entsprechend lautet dann auch die rechts davon stehende zusätzliche numerische Beschriftung (z.B. "5von5").
Die Kosten der einzelnen Verbindungen werden analog durch die Höhe eines Schiebereglers (Sliders) codiert. Die Schieberegler für die einzelnen Verbindungen werden untereinander am Bildschirm präsentiert. Dabei werden die zu einem Ausgangsort gehörigen Verbindungen jeweils nacheinander dargestellt; um die Übersichtlichkeit etwas zu erhöhen, sind die zu je einem Ausgangsort gehörigen Verbindungen durch Trennstriche optisch voneiander abgehoben.
Links von dem Slider befinden sich die Angabe der Verbindung, auf die sich dieser Slider bezieht und eine numerische Nennung der Kosten dieser Verbindung (z.B. "A1 --> B1 (Kosten: 15)"). Mit diesem Slider kann die Versuchsperson die Anzahl der auf dieser Verbindung zu vergebenden Einheiten einstellen, indem sie mit der Maus auf den Schieberegler klickt und bei gedrücktem Mausknopf diesen zu dem gewünschten Wert hin zieht. Um das genaue Einstellen eines Wertes zu ermöglichen, wird der während des Einstellens der momentan erreichte Wert rechts von dem Schieberegler angezeigt; außerdem wird durch einen Stern kenntlich gemacht, daß es sich um einen temporären Wert handelt (also z.B. "Wert: *2"). Wird der Mausknopf dann losgelassen, so wird der in diesem Moment eingestellte Wert als der neue Wert verwendet und entsprechend auch rechts von dem Schieberegler angezeigt, z.B. durch "Wert: 2". Die Schieberegler werden bei jeder Aufgabe so "geeicht", daß am rechten Anschlag der bei dieser Aufgabe maximal mögliche Wert liegt und links Null; das dazwischenliegende Intervall wird auf die zwischen diesen Extremwerten liegenden Zahlen gleichmäßig aufgeteilt.
Nachdem nun ein Wert auf die dargestellte Weise eingegeben worden ist, wird zuerst überprüft, ob er das maximal noch verfügbare Angebot an dem zugeordneten Ausgangsort oder den maximal noch benötigten Bedarf an dem entsprechenden Zielort übersteigt; ist dies der Fall, wird der Wert wiederum auf den maximal möglichen herabgesetzt: der Regler springt automatisch auf den größten sinnvollen Wert zurück. Auch hier ist es also so, daß keine Werte für die Anzahl der zu transportierenden Einheiten eingestellt werden können, die das noch verfügbare Angebot oder den noch benötigten Bedarf übersteigen. Erst nach Beendigung der Eingabe werden auch die Balken, die das verfügbare Angebot und den benötigten Bedarf codieren, zusammen mit ihrer Beschriftung auf den neuesten Stand gebracht.
Auch unter dieser Bedingung existiert ein Schalter mit der Aufschrift "fertig", der die Vollendung der Lösung signalisieren soll. Er wirkt genauso wie der gleich beschriftete Schalter in der Matrix-Bedingung.
Die Äquivalenz der beiden Bedingungen
Es wurde - mit Ausnahme der unten geschilderten Variationen - versucht, in beiden Bedingungen genau die selbe Information darzubieten. Die Kosten werden in der analogen Bedingung explizit genannt und durch die Höhe der Schieberegler codiert. In der Matrix-Bedingung stehen ihre numerischen Werte ebenfalls zusammen mit einer graphischen Codierung in der Breite eines Rechtecks in den einzelnen Zellen der Matrix. Die relativen Unterschiede bei verschiedenen Kosten sind aber nicht sehr deutlich: Den meisten Versuchspersonen fiel der Zusammenhang zwischen der unterschiedlichen Breite/Dicke und der Höhe der Kosten erst auf, nachdem sie vom Versuchsleiter darauf hingewiesen wurden.
Das Angebot und der Bedarf in den einzelnen Orten werden in der graphischen Bedingung sowohl graphisch (durch die Balken) als auch numerisch angezeigt; in der Matrix-Bedingung sind sie dagegen nur numerisch zu sehen. Es ist unbedingt nötig, daß die genauen Angebots-, Bedarfs- und Kostenwerte numerisch angezeigt werden, da sonst kein exaktes Ablesen und Einstellen gewünschter Werte möglich wäre.
Bei beiden Bedingungen sind Angebot und Bedarf auf dem Bildschirm räumlich von den Kostenwerten und den momentan eingestellten Werten abgetrennt, so daß ein ständiges Hin- und Herblicken bei der Lösungssuche erforderlich wird.
Die Unterschiede zwischen den beiden Bildschirmdarstellungen
Folgende Unterschiede zwischen den Bildschirmpräsentationen treten auf: Bei der Grafik-Bedingung werden die Werte für das verbleibende Angebot und den verbleibenden Bedarf zusätzlich noch durch einen Balken visualisiert. Dieser Balken ist deutlich sichtbar; deshalb kann sofort erkannt werden, wo das meiste Angebot zur Verfügung steht bzw. an welchem Ort der meiste Bedarf besteht. Außerdem kann sofort erkannt werden, wenn an einem Ort kein Angebot/Bedarf mehr vorhanden ist. Vor allem gegen Ende einer Aufgabenlösung, wenn nur noch in einem Ort Angebot vorhanden ist und in einem entsprechendem Ort Bedarf (die sich genau entsprechen müssen, da die Lösungen immer genau aufgehen (die Aufgaben wurden so konstruiert)), erkennt man die "zusammengehörigen" Orte sofort. Durch die zusätzliche Visualisierung tritt also eine gewisse Erleichterung bei der Problemlösung ein.
In der Matrix-Bedingung dagegen werden die Werte für das restliche Angebot und den übrigen Bedarf als Ziffern in einer Spalte untereinander angezeigt. Die einzelnen Zeilen der Spalte stehen zudem noch recht dicht untereinander. Es ist deshalb mit einem gewissen Aufwand verbunden, den zu einem bestimmten Ort gehörigen Wert herauszusuchen. Insbesondere bedeutet es auch dann einen relativ hohen Aufwand, wenn der gesuchte Wert Null ist, also eigentlich gar nicht weiter betrachtet werden müßte. Im Gegensatz hierzu fallen bei der graphischen Bedingung solche Werte durch den "fehlenden" Balken sofort auf. Auch wenn der höchste (oder niedrigste) Wert beim Angebot oder Bedarf gesucht werden soll (was laut den Verbalprotokollen bei manchen Versuchspersonen Teil ihrer Lösungsstrategie war), müssen numerische Vergleiche durchgeführt werden, die mehr Zeit und Platz im Arbeitsgedächtnis in Anspruch nehmen.
In der Grafik-Bedingung ist außerdem ein bereits abgearbeitetes Feld deutlich sichtbar, da sich dort der Schieberegler nicht mehr in der Ausgangsposition befindet. Die Ausgangsstellung des Schiebereglers kann als "gute Gestalt" betrachtet werden; außerdem dürfte es sich um die am häufigsten von der Versuchsperson gesehene Variante handeln (am Beginn einer Aufgabe stehen alle Regler in dieser Position; am Ende immer noch einige!). Ein sich nicht in der Ausgangsposition befindender Schieberegler signalisiert der Versuchsperson, daß die entsprechende Verbindung nicht mehr in die Überlegungen eingeschlossen werden braucht. In diesem Zusammenhang muß davon ausgegangen werden, daß prinzipiell auf jeder Verbindung nur einmal etwas vergeben wird; werden auf einer Verbindung mehrere unterschiedliche Werte eingegeben, so enthält die Lösung letztlich nur den zuletzt eingegebenen Wert. Deshalb sind alle zuvor eingegebenen Zahlen als überflüssige Schritte zu betrachten.
Folgende Folgerungen lassen sich aus den dargestellten Unterschieden ziehen: Der Vorteil der Salienz der bereits bearbeiteten Felder (der nur in der graphischen Bedingung herrscht) liegt vor allem darin, daß die Versuchsperson diese Verbindungen bei der weiteren Suche nach der Lösung nicht mehr in Erwägung ziehen muß. Auf diese Weise kann sie ihren Suchraum entsprechend verkleinern. Dies wäre zwar grundsätzlich auch in der Matrix-Bedingung möglich, aber dort kann man die bereits bearbeiteten Felder erst als solche erkennen, nachdem der numerische Wert der bereits vergebenen Einheiten encodiert und als von Null verschieden erkannt wurde. Dazu wird ein Teil der Kapazität des Arbeitsgedächtnisses beansprucht. Dieses Encodieren sollte außerdem mehr mit der eigentlichen Lösungsfindung - zu der ja auch mit numerischen Werten "hantiert" wird - interferieren als das rein visuelle Suchen von auffälligen Schiebereglern.
Ein weiterer Unterschied in der Work-Load kann sich daraus ergeben, daß in der Grafik-Bedingung die Orte, an denen kein Angebot mehr vorhanden ist bzw. kein Bedarf mehr benötigt wird, leicht erkennbar sind, da dort kein dunkler Balken mehr sichtbar ist. Auch hier entfällt also das Encodieren numerischer Information.
Bei der Anwendung mancher der von den Versuchspersonen in der postexperimentellen Befragung genannten Strategien muß das höchste noch verfügbare Angebot bzw. der größte noch benötigte Bedarf gefunden werden. Dies kann bei den Balken rein visuell geschehen, ohne daß dazu numerische Information encodiert und verglichen werden muß. In der Matrix-Bedingung ist dies dagegen erforderlich und trägt zu einer erhöhten Belastung des Arbeitsgedächtnisses bei.
Da in der Grafik-Bedingung ein Teil der relevanten Informationen rein visuell encodiert werden kann, während in der Matrix-Bedingung zur Aufnahme der selben Informationen erst Zahlen abgelesen und codiert werden müssen, besteht - im Sinne der Multiple-Ressource Theorie von Wickens (1992) - die Möglichkeit, daß bei der erstgenannten Bedingung auch deshalb eine geringere Work-Load auftritt, weil sich die Belastung auf verschiedene Komponenten des Arbeitsgedächtnisses verteilt, die wenig miteinander interferieren.
Die Work-Load ist in der Matrix-Bedingung aus den hier aufgeführten Gründen somit höher als in der Grafik-Bedingung. Dadurch sollte die Erstellung einer Lösung erschwert werden; dies gilt insbesondere, wenn dazu nicht eine einfache Strategie verwendet wird, die keine weitere Suche erfordert.
Nach Card, Moran und Newell (1990, S. 332) sollten zum Eingeben der einzelnen Lösungsschritte in der Matrix-Bedingung durchschnittlich jeweils maximal 3.10 Sekunden erforderlich sein: Zuerst wird mit der Maus eine Verbindung angewählt; dann muß mit der Tastatur der numerische Wert der zu vergebenden Einheiten eingegeben werden. Bei diesem Wert handelte es sich in allen Fällen um eine einzige Ziffer, wie sich in den Daten zeigte. Folgende Komponenten tragen zur reinen Eingabezeit bei:
Im ungünstigsten Fall (Abschließen durch Anklicken von "ok" und sehr langsames Tippen) wird also nur ein Zeitbedarf von 3.10 Sekunden vorhergesagt. Die theoretische Zeit für das Eingeben der Werte in der Grafik-Bedingung besteht dagegen nur aus einer Komponente: dem Zeigen auf ein Ziel mit der Maus, das nach Card, Moran und Newell (1990) etwa 1.10 sec in Anspruch nehmen sollte. Die Komponente des homing entfällt unter dieser Bedingung, da die Zeit erst ab dem Moment gestoppt wird, an dem der Schieberegler für die jeweilige Verbindung angewählt wurde.
In dem hier beschriebenen Experiment sollten vor allem die Auswirkungen der folgenden drei experimentellen Variationen untersucht werden: Bei der Bildschirmpräsentation kann es sich entweder um die Matrix-Bedingung oder um die Grafik-Bedingung handeln (siehe oben).
Bei den "Gruppen" wurden die Experimental-Gruppe, die die Aufgaben ohne Hinweise zur optimalen Lösungsstrategie lösen sollte, und die Kontroll-Gruppe, der zu Beginn des Experiments die oben beschriebene optimale Strategie erklärt wurde, verglichen.
Schließlich sollte noch untersucht werden, wie sich lineare Transformationen der einzelnen Kostenwerte, die zu neuen Kosten führen, wobei aber die Struktur der Aufgaben (ihr Problemraum, ihr Lösungsraum etc.) erhalten bleibt, auswirken. Im folgenden wird dieser Faktor als isomorphe Aufgabenvariation bezeichnet.
Für die statistische Auswertung der Ergebnisse der Versuchspersonen wurden folgende abhängige Variablen verwendet:
Die Lösungszeiten bestehen aus den gesamten zur Lösung der jeweiligen Aufgaben benötigten Zeiten: Es handelt sich um die Zeiten von der Präsentation der Aufgaben bis zur Beendigung der Lösung, ohne die Zeiten, die zum Aufbau des Bildschirms benötigt werden. Die Lösungszeiten setzen sich zusammen aus den Eingabezeiten, die aus den Zeiten vom Anwählen einer Verbindung bis zum Abschluß der entsprechenden Eingabe bestehen, und den Bearbeitungszeiten, die aus dem restlichen Anteil der Lösungszeiten bestehen.
Die Distanzen zum Optimum errechnen sich aus der Differenz zwischen den Kosten der Lösung der Versuchsperson und den Kosten der optimalen Lösung. Um die Vergleichbarkeit dieser abhängigen Variable zwischen den verschiedenen Varianten der Aufgaben zu gewährleisten, wurden die Distanzen zum Optimum folgendermaßen normiert: Der Quotient aus den tatsächlichen Kosten und den Kosten der optimalen Lösung wurde gebildet und mit 100 multipliziert. Dieser Wert ist unabhängig von der absoluten Höhe der Kosten.
Die Anzahl der Schritte besagt, wie viele Operatoranwendungen von der Versuchsperson ausgeführt wurden, um die Lösung zu erstellen.
Die subjektiven Distanzen zum Optimum werden nach der Bearbeitung jeder Aufgabe von den Versuchspersonen erfragt: Die Kosten der optimalen Lösung werden angezeigt und die Versuchsperson sollte daraufhin schätzen, welche Kosten ihre Lösung verursacht. Diese subjektive Distanz zum Optimum wird genauso normiert wie die tatsächliche Distanz zum Optimum.
Die subjektive Schwierigkeit der Aufgaben wird am Ende jeder Aufgabe von den Versuchspersonen erfragt: Sie sollten sie auf einer fünfstufigen Skala einschätzen.
Die Eingabezeiten in der Matrix-Bedingung sollten für beide Gruppen nach den Vorhersagen von Card, Moran und Newell (1990) etwa bei 3.10 Sekunden liegen, in der Grafik-Bedingung ungefähr bei 1.10 Sekunden (Hypothese 1a).
Es ist zu erwarten, daß die Lösungszeit in der experimentellen Matrix-Bedingung höher liegt als in der experimentellen Grafik-Bedingung, da dort eine höhere Work-Load herrscht (Hypothese 1b; siehe oben). Die höhere Work-Load sollte dazu führen, daß öfter Elemente aus dem Arbeitsgedächtnis verloren gehen und neu codiert werden müssen; dafür wird zusätzliche Zeit beansprucht. Wenn die Instruktion in den Kontrollgruppen, die optimale Strategie anzuwenden, befolgt wurde, sollten dort die Lösungszeiten niedriger liegen als in den Experimental-Gruppen (Hypothese 1c), da die einzelnen Schritte der Lösung nicht erst geplant werden müssen.
Die Lösungszeiten sollten im Verlauf des Experimentes bei allen Bedingungen (Matrix und Grafik; Experimental- und Kontroll-Gruppe) abnehmen (Hypothese 1d), da einerseits die Übung im Umgang mit der Schnittstelle zum Computer zu schnellerem Encodieren der Aufgabenstellung und Eingeben der Lösung führen sollte und andererseits der Erwerb von Strategien die Planungszeiten verringern sollte.
Aufgrund der Bildschirmpräsentation sind keine Unterschiede in der Güte der Lösungen zu erwarten (Hypothese 2a), da der für die Güte wesentliche Faktor, die Rangreihe der Kosten, bei beiden Varianten gleich salient - durch die exakt gleiche Breite bzw. Höhe eines Rechteckes - dargestellt wird.
Da bei den Experimental-Gruppen damit zu rechnen ist, daß das wiederholte Lösen der Aufgaben zum Erwerb effizienter und zum Ausscheiden ungünstiger Strategien führt, sollten die Lösungen im Verlauf des Experiments besser werden (Hypothese 2b). Die bei Anwendung von Strategien reduzierte Work-Load sollte außerdem zu einer Verringerung der bei der Bearbeitung der Aufgaben auftretenden Fehlerhäufigkeit führen und somit ebenfalls zu einer Verbesserung der Lösungsgüte beitragen.
Es ist zu erwarten, daß für die Lösung schwieriger Aufgaben, also derjenigen Aufgaben, die im Allgemeinen ungünstiger gelöst wurden, auch relativ lange gebraucht wird (Hypothese 2c), weil anzunehmen ist, daß die Versuchsperson bemerkt, wenn eine Lösung teuer zu werden droht und sie deswegen länger über die möglichen Schritte nachdenkt bzw. mehr Alternativen überdenkt, um ungünstige Lösungen zu vermeiden.
Da in der Grafik-Bedingung das Eingeben eines Wertes wesentlich weniger Aufwand verursacht, wird unter diesen Umständen möglicherweise die Eingabe nicht so exakt getätigt und es wird nicht so weit vorausgeplant wie in der Matrix-Bedingung, weil ein potentiell erforderliches Ausbessern wesentlich weniger Aufwand erforderlich macht. Deshalb sollte bei der Grafik-Bedingung öfter das Ausbessern bereits getätigter Eingaben stattfinden. Diese Überlegung führt wiederum dazu, daß in dieser Bedingung mehr Schritte zu erwarten sind (Hypothese 3a).
In den Kontroll-Gruppen sollten durchschnittlich weniger Schritte ausgeführt werden als in den Experimental-Gruppen (Hypothese 3b), weil eine bekannte optimale Lösungsstrategie dazu führen sollte, daß weniger ungünstige und somit ausbesserungsbedürftige Teillösungen produziert werden. Die Ausbesserung einer Lösung würde aber zusätzliche Schritte erforderlich machen.
Mit zunehmender Übung bei der Lösung der Aufgaben ist der Erwerb von effizienten Strategien zu erwarten; bei der Abarbeitung von bekannten Strategien sollten weniger Fehler auftreten, da seltener sich als ungünstig erweisende Teillösungen produziert werden, die dann ausgebessert werden müssen. Dies sollte dazu führen, daß im Verlauf des Experiments in den Experimental-Gruppen weniger überflüssige Schritte auftreten (Hypothese 3c).
Bei den Kontroll-Gruppen sollten die Versuchspersonen ihre Lösungen für besser halten als bei den Experimental-Gruppen (Hypothese 4a), da die Versuchspersonen in der ersteren Bedingung wissen, daß sie die optimale Strategie verfolgen. Die Versuchspersonen sollten die Kosten der jeweiligen Lösung mit zunehmender Übung besser schätzen können (Hypothese 4b), da nach jeder Aufgabe Rückmeldung über die entstandenen Kosten gegeben wird.
Am Ende jeder Aufgabe stand die Frage, wie schwer die Versuchspersonen die jeweilige Aufgabe empfunden hätten. Die empfundene Aufgabenschwierigkeit sollte mit der Anzahl möglicher Zustände bei der Lösungssuche, also dem Umfang des Problemraums zusammenhängen (Hypothese 5a), wenn tatsächlich eine systematische Suche in dem jeweiligen Problemraum stattfinden würde.
Wenn die Versuchsperson nach der Bearbeitung einer Aufgabe dazu aufgefordert wird, deren Schwierigkeit zu beurteilen, kann sie zur Abgabe ihres Urteils verschiedene Kriterien verwenden: Es ist zu erwarten, daß eine Aufgabe für um so schwieriger gehalten wird, je mehr Zeit ihre Lösung in Anspruch genommen hat (Hypothese 5b) und je mehr Schritte für ihre Lösung benötigt wurden (Hypothese 5c). Außerdem sollten die Aufgaben, von denen die Versuchsperson meint, sie seien schlecht gelöst worden, als schwieriger eingestuft werden (Hypothese 5d).
Es wurden durch lineare Transformation der Kostenwerte drei Klassen von Aufgaben erzeugt: Die Variante klein-eng verwendete niedrige Kosten zwischen 6 und 15; in der Variante groß-eng traten Kosten zwischen 56 und 65 auf und für die Variante groß-weit wurden Kosten zwischen 27 und 63 gewählt, die jeweils einen Abstand von 4 Einheiten hatten. Durch die Verwendung der verschiedenen Varianten der Aufgaben wurde es möglich, den Versuchspersonen von jeder Aufgabe drei isomorphe Versionen zu präsentieren.
Die für mentale Arithmetik benötigte Zeit hängt von der Größe der auftretenden Zahlen ab; die für Größenvergleiche benötigte Zeit ebenfalls. Die zur Lösung einer Aufgabe benötigte Zeit sollte somit - wenn zur Lösungsfindung gerechnet wurde - bei den Experimental-Gruppen von der Höhe der Kosten und wegen der unterschiedlichen Schwierigkeit bei der Rangreihenbildung von dem Abstand der Kosten abhängen (Hypothese 6a).
Es ist auch zu erwarten, daß sich die einzelnen Aufgaben (Aufgabe1 bis Aufgabe6) in den Experimental-Gruppen in ihrer durchschnittlichen Lösungszeit unterscheiden, da ihnen jeweils eine unterschiedliche Struktur zugrunde liegt und sie somit unterschiedlich schwierig zu lösen sein sollten (Hypothese 6b). In den Kontroll-Gruppen sollten sich dagegen kaum Unterschiede aufgrund der verschiedenen Aufgaben ergeben, da dort immer eine vorgegebene Strategie abgearbeitet werden soll (Hypothese 6c), auf deren Anwendung die Struktur des Problemraums keinen Einfluß hat.
Die Häufigkeit der Anwendung von Strategien sollte im Verlauf des Experimentes zunehmen (Hypothese 7): Es ist anzunehmen, daß die Versuchspersonen anfangs eher verschiedene Alternativen ausprobieren, bis sie eine befriedigende Lösungsstrategie finden, die sie dann mehr oder weniger beibehalten. Außerdem sollten die Versuchspersonen versuchen, ihren Aufwand zur Lösung der Aufgaben möglichst gering zu halten; dies ist am einfachsten möglich, indem eine bestimmte Strategie immer angewendet wird, so daß die Lösung der Aufgaben kein Problem, sondern nur noch eine abzuarbeitende Aufgabe darstellt.
Es ist aber schwierig, die Anwendung von solchen Strategien nachzuweisen, die nur teilweise die Zugfolge spezifizieren und den restlichen Teil der Zugfolge von der Intuition des Problemlösers und der konkreten Aufgabe abhängig machen.
Über Unterschiede zwischen den Bildschirmpräsentationen lassen sich an dieser Stelle keine Vorhersagen treffen. Es ist aber davon auszugehen, daß sich Experimental- und Kontrollgruppen bezüglich der Anwendung der optimalen Strategie unterscheiden werden, da ja die Versuchspersonen in der Kontrollgruppe explizit instruiert wurden, nach der optimalen Strategie vorzugehen, während in der Experimental-Gruppe erst eine geeignete Vorgehensweise herausgefunden werden muß.
Es ist kaum zu erwarten, daß sich die verschiedenen Bildschirmpräsentationen darin unterscheiden, in wie weit die jeweiligen Probanden die Lösungswege, die sie einschlugen, explizit verfügbar machen und verbalisieren können.
Es ist aber damit zu rechnen, daß die Versuchspersonen erst im Laufe der Befragung eine Strategie finden oder rekonstruieren, wenn vorher Strategien nur implizit angewandt wurden. Deshalb sollten sie im Verlauf der Befragung die angeblich angewandte Strategie besser verbalisieren können (Hypothese 8). Dies bedeutet, daß die verbalisierten Strategien nicht unbedingt den tatsächlich angewandten entsprechen müssen.
Dem Experiment liegt ein vierfaktorielles Design mit folgenden, im weiteren ausführlich dargestellten Faktoren zugrunde:
Die Aufgabe und isomorphe Aufgabenvariation waren within-subject Faktoren, Bildschirmpräsentation und Gruppe between-subject Faktoren. Die verschiedenen abhängigen Variablen wurden im Hypothesenteil dargestellt.
An dem Experiment nahmen 54 Versuchspersonen, die an verschiedenen Fakultäten der Universität Regensburg studieren, teil; es handelte sich überwiegend um Studenten der Psychologie. Ihr Alter lag zwischen 19 und 39. 20 Versuchspersonen bearbeiteten die Aufgaben in der experimentellen graphischen Bedingung, 20 Versuchspersonen in der experimentellen Matrix-Bedingung. Jeweils 9 Versuchspersonen hatten die Aufgaben in der Matrix- und in der Grafik-Kontrollgruppe zu lösen. Die Versuchspersonen, die sich selbst in eine Liste verfügbarer Termine eintrugen, wurden entsprechend der Reihenfolge der Termine abwechselnd der graphischen Bedingung oder der Matrix-Bedingung zugewiesen; die Zuordnung zu den einzelnen Gruppen kann also als zufällig betrachtet werden. Keine der an dem Experiment teilnehmenden Versuchspersonen gab an, mit Aufgaben der gestellten Art vertraut zu sein.
Jeder Versuchsperson wurden insgesamt 21 der oben dargestellten Aufgaben zur Transportoptimierung präsentiert. Bei jeder dieser Aufgaben gab es genau drei Ausgangsorte und drei Zielorte; die Aufgaben waren so konstruiert, daß es genau eine optimale Lösung gab. Die ersten drei Aufgaben, die nicht in die Auswertung eingingen, waren zum Vertraut-Werden mit der Bildschirmpräsentation und den Eingabe-Mechanismen gedacht; bei diesen betrug das Gesamtangebot (bzw. der Gesamtbedarf) 10 Waggons. Diese ersten drei Aufgaben wurden in einer festen Reihenfolge präsentiert. Bei den 18 eigentlichen Aufgaben lagen dann das Gesamtangebot bzw. der Gesamtbedarf konstant bei 20 Waggons.
Die 18 kritischen Aufgaben, die in randomisierter Reihenfolge präsentiert wurden, setzten sich aus sechs Aufgaben zusammen, die in jeweils drei isomorphen Varianten präsentiert wurden. Folgende Klassen von Variationen wurden verwendet:
Die Faktorstufe mit den kleinen, weit auseinander liegenden Kosten konnte nicht realisiert werden, da die größte der neun weit (also vier Einheiten) auseinander liegenden Zahlen mindestens 37 betragen würde, was keine kleine Zahl mehr darstellt.
Insgesamt wurden sechs wirklich verschiedene Aufgaben präsentiert. Die Größe des Problemraums dieser unterschiedlichen Aufgaben variierte zwischen 121996 und 355778; die Anzahl der gültigen Lösungen schwankte zwischen 145 und 412. Die Gleichheit der isomorphen Varianten wurde von den Versuchspersonen nicht bemerkt, wie sich in der anschließenden Befragung zeigte.
Instruktionen und Einführung
Die Versuchspersonen nahmen einzeln an dem Experiment, das durchschnittlich 90 bis 120 Minuten dauerte, teil. Nachdem der Computer eingeschaltet war, sollte die Versuchsperson die Instruktionen lesen. Die Instruktionen für die Versuchspersonen in der Grafik-Bedingung sind in Anhang C zu sehen, die für die Matrix-Bedingung in Anhang D. Während die Instruktionen gelesen wurden, war auf dem Bildschirm zu lesen: "Bitte lesen Sie die Instruktionen und drücken Sie dann die Taste īfertigī". In den schriftlichen Instruktionen wurde zuerst die Aufgabenstellung anhand eines Beispiels geschildert; die optimale Lösung für das Beispielproblem war ebenfalls angeführt. Dieses Beispiel war in eine Cover-Story aus dem Bereich des Bahntransports gekleidet: Leere Waggons sollten von den Ausgangsorten an die Zielorte transportiert werden. Der letzte Teil der schriftlichen Instruktionen beschrieb, wie die Aufgabenstellung am Bildschirm präsentiert werden wird und wie die Versuchsperson Werte eingeben kann. Dieser Teil der Instruktionen unterschied sich bei der graphischen Bedingung von der Matrix-Bedingung.
Wenn die Instruktionen gelesen waren, mußte die Versuchsperson mit der Maus einen Schalter am Bildschirm mit der Aufschrift "START" betätigen. Dann erschien die erste Aufgabe. Der Versuchsleiter, der während des gesamten Experiments im Raum anwesend blieb, erklärte nun nochmals den Bildschirmaufbau und die Eingabemechanismen anhand des konkreten Beispiels. Alle Fragen der Versuchsperson wurden beantwortet. Erst wenn die Versuchsperson zu erkennen gab, daß sie die Problemstellung und die Eingabemechanismen verstanden habe, wurde mit der Lösung der übrigen Aufgaben begonnen.
Abarbeitung der Aufgaben
Nachdem für diese erste Aufgabe eine Lösung erstellt und der Schalter "fertig" betätigt worden war, erschien, wie auch bei allen weiteren Aufgaben, folgende Aufforderung zur Kostenschätzung: "Wie teuer glauben Sie, ist die eingegebene Lösung? (Optimum: 358)", wobei der als Optimum bezeichnete Wert die Kosten der billigsten Lösung der gestellten Aufgabe bezeichnete. Bei der Bearbeitung der ersten Aufgabe wurde die Versuchsperson an dieser Stelle nochmals mündlich instruiert, diesen Wert zu schätzen und ihn nicht auszurechnen. Nachdem dieser Wert eingegeben worden war, wurde überprüft, ob es sich um eine natürliche Zahl handelte, die größer war als das angegebene Optimum; war dies nicht der Fall, erschien das Dialogfenster mit der oben gezeigten Aufforderung erneut.
Wenn nun ein gültiger Wert für die Schätzung der Kosten eingegeben war, erschien anschließend ein Dialogfenster mit der Frage nach der Aufgabenschwierigkeit "Wie schwer war diese Aufgabe?" und einer Reihe von Schaltflächen die folgende Aufschriften trugen: "sehr schwer", "schwer", "mittel", "leicht" und "sehr leicht". Die Versuchspersonen wurden an dieser Stelle bei der Bearbeitung der ersten Aufgabe mündlich instruiert, diese Aufgabe als mittel-schwierig zu betrachten und bei den folgenden Aufgaben anzugeben, wie schwer diese im Vergleich zu dieser ersten Aufgabe seien. Die erste Aufgabe wurde somit zum Standard bei der Beurteilung der Aufgabenschwierigkeit erklärt. Dieses Dialogfenster verschwand, wenn eine der Kategorien angewählt wurde.
Als Abschluß der Bearbeitung einer Aufgabe erhielt die Versuchsperson Feedback bezüglich ihrer Lösung der gerade bearbeiteten Aufgabe. Wenn diese Aufgabe optimal gelöst worden war, erschien ein Dialogfenster mit dem Inhalt: "Gratuliere! Dieser Lösungsvorschlag ist der Optimale"; war die Lösung nicht optimal, enthielt das Fenster einen entsprechenden Text der folgenden Art: "Dieser Lösungsvorschlag ist nicht der optimale. Wert der Lösung: 631 (Optimum: 579)". Der angegebene Wert der Lösung wurde aus der Kosten der vorliegenden Lösung berechnet; das Optimum waren wieder die Kosten der billigsten möglichen Lösung. Wenn bei diesem Dialogfenster der Schalter mit der Aufschrift "ok" oder die Eingabetaste betätigt wurden, erschien die nächste Aufgabe (bzw. die Meldung: "Vielen Dank! Das Experiment ist hier zuende", wenn die zuvor bearbeitete Aufgabe die letzte war).
Den Versuchspersonen in der Kontrollgruppe wurde nach dem Abarbeiten der ersten Aufgabe und noch bevor die zweite Aufgabe präsentiert wurde, eine schriftliche Erklärung der optimalen Strategie (siehe Anhang E) zu lesen gegeben; nachdem sie diese gelesen hatten, wurden eventuelle Fragen der Versuchspersonen zu der Strategie beantwortet.
Bei der Bearbeitung der Aufgaben konnte die Versuchsperson die Anzahl der zu transportierenden Einheiten für jede Verbindung zwischen Ausgangsort und Zielort in beliebiger Reihenfolge eingeben oder bestehende Werte abändern. Dabei wurde, wenn eine bestimmte Verbindung zur Eingabe eines neuen Wertes gewählt wurde, folgendes mitprotokolliert:
Wenn die Versuchsperson "fertig" drückte, wurden schließlich die vorgeschlagene Lösung und die seit der letzten Aktion vergangene Zeit mitprotokolliert. Handelte es sich um eine ungültige Lösung, wurde dies im Protokoll vermerkt, es erschien der oben beschriebene Hinweis und die Aufgabe mußte weiter bearbeitet werden. Handelte es sich um eine gültige Lösung, wurden ihre Kosten im Protokoll abgelegt. War die Lösung optimal, wurde ebenfalls ein Hinweis darauf in das Protokoll geschrieben. Für die Versuchsperson ging es wie oben dargestellt mit den Fragen zur Kostenschätzung und Aufgabenschwierigkeit weiter.
Die postexperimentelle Befragung
Nachdem die letzte Aufgabe bearbeitet worden war, wurden die Versuchspersonen der Experimental-Gruppe zuletzt nach ihrer Vorgehensweise beim Lösen der Aufgaben befragt. Dazu wurden allen Versuchspersonen die selben Fragen gestellt (siehe Anhang F) und ihre Antworten wurden mit einem Casettenrecorder aufgezeichnet und später transkribiert.
Die Fragestellungen wurden so konzipiert, daß sich die Versuchspersonen tatsächlich an die Abarbeitung der Aufgaben erinnern sollten und nicht versuchen sollten, eine Lösung neu zu konstruieren; dazu wurden die Hinweise von Ericsson und Simon (1984) aufgegriffen.
4. Einzelergebnisse und ihre Diskussion
Für die statistischen Auswertungen wurde ein Signifikanzniveau von .05 festgelegt. Dies bezieht sich auf alle im folgenden dargestellten Auswertungen mit Ausnahme derjenigen, bei denen ein abweichendes Signifikanzniveau gesondert vermerkt wird. Die jeweils angegebenen Maximal-Wahrscheinlichkeiten p beziehen sich auf die Wahrscheinlichkeiten, daß die jeweiligen Ergebnisse zufällig zustandegekommen sind. Für die Anwendung der Varianzanalysen wurde nicht überprüft, ob die Daten normalverteilt sind, da "the F statistic is robust with respect to the normality assumption. Robust means that the actual a is very close to the nominal a " (Stevens, 1992, S. 238; Hervorhebung im Text). Da es sich jeweils um proportionale Stichprobengrößen handelte (bei denen sich Verletzungen der Varianzhomogenität kaum bemerkbar machen; siehe z.B. Stevens, 1992), wurde die Voraussetzung der Varianzhomogenität nur dann überprüft, wenn die Unterschiede in der Varianz selbst von Interesse waren.
Die als "Eingabezeit" bezeichnete Zeit besteht aus dem Intervall zwischen dem Anwählen einer Verbindung (auf der transportiert werden soll) durch einen Mausklick und dem Abschließen der Eingabe, nachdem der gewünschte Zahlenwert eingegeben bzw. eingestellt wurde. Die dafür von Card et al. (1990) vorhergesagten Werte (Hypothese 1a) konnten nicht bestätigt werden, da der Mittelwert für die Eingabezeit in der Matrix-Bedingung mit über 6 Sekunden deutlich über dem vorhergesagten Wert von maximal 3.1 Sekunden liegt. Dies liegt allerdings daran, daß zu den als Eingabezeiten gemessenen Zeitintervallen auch andere Komponenten beitragen, die nicht mit der eigentlichen Eingabe zusammenhängen. Dies zeigt sich an mehreren Indizien:
Die Varianz der Eingabezeiten unterscheidet sich bei Anwendung eines F-Tests auf Gleichheit von Varianzen (cf. Keppel, 1982) sowohl in der Experimental-Bedingung (F(19;19) =4.6497; p < .001) als auch in der Kontroll-Bedingung (F(8; 8) = 50.7581; p < .001) sehr signifikant zwischen den verschiedenen Bildschirmpräsentationen. Dieser Unterschied kommt dadurch zustande, daß in der Matrix-Bedingung relativ oft sehr lange Eingabezeiten auftreten (deutlich über 10 Sekunden, siehe Tabelle 1).
Die Voraussetzung der Varianzhomogenität, die für Varianzanalysen besteht, ist in diesem Fall verletzt. Da sich aber Verletzungen dieser Voraussetzung, vor allem bei proportionalen Stichprobengrößen (wie sie hier vorliegen), nicht sehr kritisch auswirken, wurde dennoch eine zweifaktorielle Varianzanalyse mit den Faktoren Bildschirmpräsentation und Gruppe berechnet; allerdings wurde dabei das Signifikanzniveau auf .01 herabgesetzt. Der Faktor Bildschirmpräsentation wirkt sich signifikant auf die Eingabezeiten aus (F(1; 54) = 153.758; p < .0005): In der Matrix-Bedingung wird wesentlich mehr Zeit zum Eingeben benötigt als in der Grafik-Bedingung. Die Differenz der Eingabezeiten zwischen den Bildschirmpräsentationen in der Kontrollgruppe ist etwa genauso hoch ist wie in der Experimental-Gruppe: Es tritt keine signifikante Interaktion zwischen der Gruppe und der Bildschirmpräsentation auf (F(1; 54) = 0.712; p = .403). Insgesamt liegen jedoch die Zeiten in den Kontrollgruppen etwas niedriger (Grafik: 0.801 (Kontrollgruppe) vs. 1.216 (Experimentalgruppe) Sekunden Mittelwert ; Matrix: 6.601 (Kontrollgruppe) vs. 7.965 (Experimentalgruppe) Sekunden Mittelwert); der Unterschied ist außerdem in der Matrix-Bedingung stärker ausgeprägt. Dieser Unterschied durch den Faktor Gruppe ist jedoch nicht signifikant (F(1; 54) = 2.500; p = .120).
Es wurde die Regression der Mittelwerte (über die Versuchspersonen) der Lösungszeiten auf die Aufgabenposition berechnet. In der experimentellen Gruppe ist der Fit des exponentiellen Modells (R2(Matrix) = 31.30%; R2(Grafik) = 34.53%) etwa genauso gut wie der Fit des multiplikativen Modells (R2(Matrix) = 19.25%; R2(Grafik) = 34.09%), das einen Verlauf nach dem sogenannten power-law zugrundelegt. Bei der Kontrollgruppe ist der Fit bei beiden Modellen zwar besser, aber auch hier zeigen sich keine deutlichen Tendenzen, die für eines der beiden Modelle sprechen würden: Das multiplikative Modell (R2(Matrix) = 76.17%; R2(Grafik) = 64.61%) paßt etwa genauso gut wie das exponentielle Modell (R2(Matrix) = 83.60%; R2(Grafik) = 62.13%).
Gemäß den Ausführungen von Newell und Rosenbloom (1981) ist für den Lernverlauf der Zeiten zur Bedienung eines Software-Interfaces ein Zusammenhang entsprechend dem power-law zu erwarten. Die Passung des entsprechenden Modells war auch akzeptabel (siehe oben). Im folgenden werde ich deshalb nur die Ergebnisse der Auswertung der Regression des Logarithmus der Eingabezeit auf den Logarithmus der Aufgabenposition betrachten.
In Abbildung 1 sind die Lernkurven für die Eingabezeit für die vier experimentellen Bedingungen zu sehen. Folgende Regressionsgleichungen nach dem multiplikativen Modell ergaben sich:
|
Grafik (experimentell): |
y = exp(0.558 * x-0.198); |
|
Matrix (experimentell): |
y = exp(2.165 * x-0.046); |
|
Grafik (Kontrolle): |
y = exp(0.160 * x-0.198) und |
|
Matrix (Kontrolle): |
y = exp(2.201 * x-0.160). |
Betrachtet man die Steigungen der Lernkurven, sollte man daraus Hinweise auf die Geschwindigkeit, mit der gelernt wird, erhalten; der Steigungsparameter der Kurven kann als Maß für die Geschwindigkeit des Lerngewinnes - als Lernparameter - interpretiert werden. Signifikante Unterschiede in den Steigungsparametern sollten mit dem von Cohen und Cohen (1983, S. 55f) dargestellten Verfahren aufgezeigt werden. Weil dieses Verfahren nur für das lineare Modell, also für die Steigungsparameter von Regressionslinien anwendbar ist, mußten sowohl die Kriteriumsvariable (Eingabezeit) als auch die Prädiktor-Variable (Aufgabenposition) logarithmisiert werden, so daß in dem so entstandenen Koordinatensystem die multiplikative Regressionsgleichung eine Gerade beschreibt. Da für diese weitergehende Betrachtung wiederum die Eingabezeiten statistisch ausgewertet werden, mußte eine a -Adjustierung des Signifikanzniveaus vorgenommen werden: Es liegt hier bei .025. Bei der graphischen Bildschirmpräsentation unterscheiden sich die Steigungsparameter der Lernkurven für die Mittelwerte der Eingabezeit zwischen der Experimental- und der Kontrollgruppe nicht signifikant (Experimental-Gruppe: -0.1978; R2 = 34.09%; Kontroll-Gruppe: -0.1979; R2 =64.61%; t(32) = 0.0018; p = .4999).

Abbildung 1: Die multiplikative Regression der Aufgabenposition auf die "Eingabezeit" für alle vier experimentellen Gruppen getrennt. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen. Die Werte auf der Abszisse (Nr.) stehen für die Position der präsentierten Aufgabe im Experiment; die Werte auf der Ordinate (Zeit) stehen für die Mittelwerte der Lösungszeiten in Sekunden bei der jeweiligen Bedingung.
Bei der Matrix-Bedingung dagegen treten deutliche Unterschiede auf: In den Kontrollgruppen wird wesentlich schneller gelernt: Die Steigung der Lernkurve für die Mittelwerte der Eingabezeit liegt deutlich höher: (Experimental-Gruppe: -0.0462; R2 = 19.25%; Kontroll-Gruppe: -0.1600; R2 =76.17%; t(32) = 3.049; p = .002). In der experimentellen Matrix-Bedingung ist der Steigungsparameter ebenfalls signifikant niedriger als in der experimentellen Grafik-Bedingung (t(32) = 3.797; p< .001). In der experimentellen Matrix-Gruppe findet also im Verlauf des Experimentes eine deutlich geringere Beschleunigung der "Eingabezeiten" statt als unter den anderen Bedingungen.
Häufigkeit der Wahl eines Feldes, auf dem nichts mehr vergeben werden kann
Wenn der Fall eintritt, daß eine Verbindung angewählt wurde, auf der nichts mehr transportiert werden kann, dann muß die Versuchsperson bei der Abarbeitung dieser Aufgabe so vorgegangen sein, daß sie zuerst eine Verbindung (nur auf Grund ihrer Kosten) aussuchte und dann erst betrachtete, wie viele Einheiten vergeben werden sollten. Dieser Fall tritt in der Matrix-Bedingung (f = .0645) häufiger auf als in der Grafik-Bedingung (f = .0588); der Unterschied ist allerdings bei weitem nicht signifikant (t(38) = 0.279; p = .782).
Wenn man allerdings beachtet, daß in der Matrix-Bedingung (bei jeder Aufgabe durchschnittlich 0.569) signifikant weniger überflüssige Schritte gemacht werden als in der Grafik-Bedingung (durchschnittlich 1.0766) (F(1; 54) = 5.218; p = .026) und dabei bedenkt, daß es sich bei der Wahl einer Verbindung, auf der nichts mehr transportiert werden kann, um einen überflüssigen Schritt handelt, dann muß man dem nicht signifikanten Unterschied in der Häufigkeit der Wahl solcher Verbindungen doch eine gewisse Bedeutung beimessen.
Verteilung der kategorisierten Eingabezeiten
|
|
Grafik (exp) |
Matrix (exp) |
Grafik (kon) |
Matrix (kon) |
|
< 2000 msec |
0,890 |
0 |
0,968 |
0,006 |
|
2000 - 3999 msec |
0,057 |
0,061 |
0,032 |
0,271 |
|
4000 - 5999 msec |
0,026 |
0,293 |
0 |
0,206 |
|
6000 - 7999 msec |
0,009 |
0,242 |
0 |
0,230 |
|
8000 - 9999 msec |
0,005 |
0,204 |
0 |
0,154 |
|
10000 - 11999 msec |
0 |
0,074 |
0 |
0,043 |
|
12000 - 13999 msec |
0 |
0,059 |
0 |
0,058 |
|
14000 - 15999 msec |
0,003 |
0,021 |
0 |
0,012 |
|
16000 - 17999 msec |
0 |
0,025 |
0 |
0,013 |
|
18000 - 19999 msec |
0,002 |
0,008 |
0 |
0,006 |
|
> 19999 msec |
0 |
0,014 |
0 |
0 |
Tabelle 1:
Die Häufigkeiten der Eingabezeiten in verschiedenen Kategorien für die verschiedenen experimentellen Gruppen. "exp" steht für die experimentellen Gruppen, "kon" für die Kontrollgruppen.
Werden die Eingabezeiten in Kategorien, die jeweils 2 Sekunden umfassen, eingeteilt und werden dann die Häufigkeiten bestimmt, mit denen die einzelnen Kategorien unter den verschiedenen experimentellen Variationen vertreten sind, erhält man die in Tabelle 1 dargestellte Verteilung der Eingabezeiten. Dort ist deutlich zu sehen, daß in der Matrix-Bedingung fast alle Eingabezeiten in Kategorien liegen, die über dem theoretisch vorhergesagten Wert (unter ungünstigen Umständen etwa 3.2 Sekunden) liegen.
Die starke Abweichung der "Eingabezeiten" in der Matrix-Bedingung von den nach dem Modell von Card, Moran und Newell (1990) vorhergesagten Zeiten und die Verteilung der Eingabezeiten, die belegt, daß in dieser Bedingung vor allem Zeitintervalle über 4 Sekunden auftreten, weisen darauf hin, daß es sich bei diesen Zeitintervallen in der Matrix-Bedingung nicht um reine Eingabezeiten handeln kann. Die aufgeführten Merkmale der Eingabezeiten lassen sich dadurch erklären, daß es sich bei den Zeiten der Grafik-Bedingung tatsächlich um reine Bedienzeiten handelt und daß das wiederholte Eingeben der Werte zu einer deutlichen Geschwindigkeitssteigerung führt. In der Matrix-Bedingung dagegen muß noch eine (mehr oder weniger konstante) Komponente hinzukommen, die auch dazu führt, daß die durch Übung bedingte Abnahme der Eingabezeit verhältnismäßig geringer ausfällt. Die zusätzliche(n) Komponente(n) könnten auch die höhere Varianz in der experimentellen Matrix-Bedingung erklären. Der Grund für diese in der Matrix-Bedingung abweichenden Werte kann an einer anderen Vorgehensweise bei der Bearbeitung der Aufgaben liegen:
Die Versuchspersonen in der Matrix-Bedingung öffneten durch Anklicken das Eingabefenster und überlegten möglicherweise manchmal erst dann, welchen numerischen Wert sie eingeben sollten. Dabei brauchten sie sich die gewählte Verbindung nicht mehr zu merken, da diese in dem Eingabefeld nochmals vermerkt war. Insofern trägt diese Vorgehensweise zu einer Entlastung des Arbeitsgedächtnisses bei.
In der Grafik-Bedingung dagegen klickten die Versuchspersonen den Schieberegler zum Einstellen des Wertes erst an, nachdem sie bereits wußten, welcher Wert eingestellt werden sollte. Ein Grund dafür ist, daß von diesem Zeitpunkt an der linke Mausknopf so lange gedrückt gehalten werden mußte, bis die Eingabe beendet war. Die unterschiedlichen Bildschirmpräsentationen und Eingabemechanismen führten also zu verschiedenen Vorgehensweisen bei der Lösung der Aufgaben.
Die hinzukommende Komponente in der Matrix-Bedingung besteht in dem Heraussuchen des zu vergebenden Wertes: Dazu muß abgelesen werden, wie viel Angebot noch vorhanden ist bzw. wie viel Bedarf noch besteht. Bei dem Ablesen und Vergleichen dieser Werte ist kaum ein größerer Geschwindigkeitszuwachs mit zunehmender Übung zu erwarten, da das Ablesen und der Größenvergleich von (maximal zweistelligen) Zahlen schon vor Beginn des Experimentes sehr geübt sein dürften und somit weitere Übung zu keiner deutlichen Geschwindigkeitssteigerung mehr führen sollte. Dies bewirkt letztendlich, daß bei der Matrix-Gruppe ein geringerer Lernzuwachs zu verzeichnen ist als bei der Grafik-Gruppe.
Dafür, daß eine Verbindung angewählt wurde, bevor die Anzahl zu vergebender Einheiten bestimmt wurde, spricht auch die in der Matrix-Bedingung etwas höhere Häufigkeit der Wahl von Verbindungen, auf denen nichts vergeben werden kann.
Bei der "Eingabezeit" handelt es sich, wie gerade gezeigt, nicht um die reine Eingabezeit, sondern zumindest in der Matrix-Bedingung kommen auch noch andere Komponenten hinzu. Da die tatsächliche Eingabezeiten nicht aus den Daten rekonstruiert werden können, muß im der theoretisch vorhergesagte Wert als Grundlage für die weiteren Überlegungen verwendet werden. Die theoretisch vorhergesagten Eingabezeiten für jede Verbindung sind relativ kurz und der Unterschied zwischen den Bildschirmpräsentationen beträgt maximal etwa 2 Sekunden. Die Mittelwerte der Gesamtlösungszeiten differieren dagegen in der Experimental-Bedingungen um über 31 Sekunden. Die vermutlich geringe Differenz aufgrund der unterschiedlichen Eingabezeiten sollte also nicht sonderlich ins Gewicht fallen. Deshalb wurden bei den weiteren Betrachtungen nur noch die gesamten Lösungszeiten ausgewertet.
Die Regression der Lösungszeit auf die Aufgabenposition erzielt bei allen untersuchten Modellen nur eine geringe Passung zwischen den vorhergesagten und den beobachteten Werten: Bei den Experimental-Gruppen übersteigt der Determinationskoeffizient R2 10% nicht. Dies liegt an den hohen Varianzen der Lösungszeiten zwischen den Versuchspersonen. Für die weiteren regressionsanalytischen Betrachtungen wurde deshalb über die Versuchspersonen gemittelt.
|
1.- 3. |
4. - 6. |
7. - 9. |
10.-12. |
13.-15. |
16.-18. |
alle |
|
|
Matrix EXP |
165,8 |
145,0 |
148,4 |
137,0 |
120,6 |
112,4 |
138,2 |
|
Grafik EXP |
120,1 |
117,2 |
105,7 |
96,4 |
79,9 |
75,3 |
99,1 |
|
EXP |
142,9 |
131,1 |
127,1 |
116,7 |
100,2 |
93,9 |
118,6 |
|
Matrix KON |
100,6 |
80,2 |
81,8 |
76,4 |
67,4 |
63,8 |
78,4 |
|
Grafik KON |
82,9 |
72,3 |
54,2 |
50,2 |
52,3 |
45,8 |
59,6 |
|
KON |
91,7 |
76,2 |
68,0 |
63,3 |
59,8 |
54,8 |
69,0 |
Tabelle2: Die durchschnittlichen Lösungszeiten
(in Sekunden) für jeweils eine Aufgabe. EXP steht für die Experimental-Gruppen, KON für die Kontrollgruppen.
Varianzanalytische Betrachtung der Lösungszeiten
In Tabelle 2 sind die Mittelwerte der Lösungszeiten für die einzelnen Gruppen jeweils über drei aufeinanderfolgende Aufgaben gemittelt dargestellt. Eine mehrfaktorielle Varianzanalyse (Block x Bildschirmpräsentation x Gruppe) mit der Lösungszeit als abhängiger Variable ergab folgende Ergebnisse: Der Effekt des Faktors Aufgabenblock (1. - 3. Aufgabe sind der Block1; 4. - 6. Aufgabe sind der Block2 usw.) ist hochsignifikant (F(5; 270) = 21.822; p < .0005). Es ist also insgesamt ein deutlicher Lerneffekt nachweisbar.
Der Faktor Bildschirmpräsentation (Matrix oder Grafik) erreicht ebenfalls Signifikanzniveau (F(1; 54) = 11.282; p < .001). Der Effekt der Bildschirmpräsentation bleibt dagegen nicht signifikant, wenn nur die Kontrollgruppen varianzanalytisch betrachtet werden: Die Berechnung einer Varianzanalyse mit dem Faktor Bildschirmpräsentation für die Kontrollgruppen (wobei, da die selben Daten wie für die oben dargestellte Varianzanalyse verwendet wurden, das Signifikanzniveau auf .025 adjustiert werden mußte) zeigt, daß der Effekt dieses Faktors nicht signifikant ist (F(1; 16) = 3.094; p = .098). Der oben aufgeführte signifikante Effekt ist somit auf Unterschiede zwischen den beiden Experimental-Gruppen zurückzuführen. Die Hypothese 1b, die für die experimentelle Matrix-Bedingung höhere Lösungszeiten postuliert, kann somit beibehalten werden.
Der Effekt des Faktors Gruppe (Experimental oder Kontrolle) ist wiederum hoch signifikant (F(1; 54) = 22.167; p < .0005). Es wirkt sich also deutlich auf die Lösungszeit aus, ob die Versuchsperson bereits zu Beginn des Experiments die optimale Lösungsstrategie kennt. Die in der Hypothese 1c vermuteten geringeren Lösungszeiten in den Kontroll-Gruppen scheinen also tatsächlich vorzuliegen.
Keine der Interaktionen zwischen diesen Faktoren erreicht auch nur annähernd Signifikanzniveau (in allen Fällen ist p > .33). Dies deutet insbesondere darauf hin, daß sich der Lernverlauf weder zwischen der Experimental-Gruppe und der Kontrollgruppe noch zwischen den Bildschirmpräsentationen signifikant unterscheidet.
Die Regression der Lösungszeiten auf die Aufgabenposition läßt sich in den beiden experimentellen Gruppen am besten durch ein exponentielles Modell beschreiben; die Passung liegt bei Verwendung des multiplikativen Modells etwas geringer:
|
Matrix (exponentiell): |
y = exp(5.15 - 0.024x); |
R^2 = 82.95%; |
|
Matrix (multiplikativ): |
y = exp(5.218 * x-0.148); |
R^2 = 69.54%; |
|
Grafik (exponentiell): |
y = exp(4.90 - 0.034x); |
R^2 = 81.63%; |
|
Grafik (multiplikativ): |
y = exp(5.0 * x-0.209); |
R^2 = 68.02%. |
Für die Mittelwerte der Versuchspersonen der Kontrollgruppen ergibt sich dagegen bei einem Modell nach dem Power-Law eine bessere Passung als nach dem exponentiellen Modell:
|
Matrix (exponentiell): |
y = exp(4.60 - 0.026x); |
R^2 = 69.82%; |
|
Matrix (multiplikativ): |
y = exp(4.70 * x-0.174); |
R^2 = 69.54%; |
|
Grafik (exponentiell): |
y = exp(4.43 - 0.039x); |
R^2 = 80.12%; |
|
Grafik (multiplikativ): |
y = exp(4.61 * x-0.270); |
R^2 = 87.69%. |
Betrachtet man die Regressionsgleichungen, die nach dem multiplikativen Modell erstellt wurden und in Abbildung 2 zu sehen sind, zeigen die Steigungsparameter bei den verschiedenen Bildschirmpräsentationen etwa gleiche Werte.
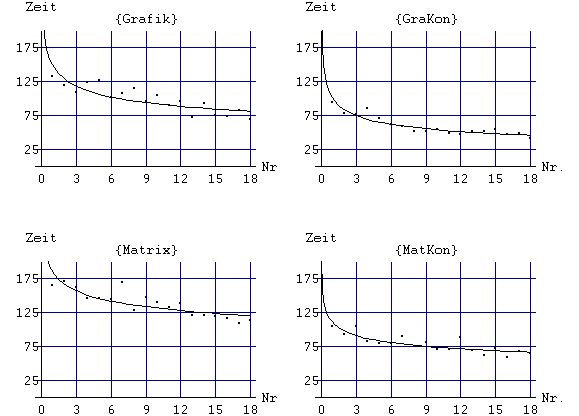
Abbildung 2: Die multiplikative Regression der Aufgabenposition auf die Lösungszeit für alle vier experimentellen Gruppen getrennt. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen. Nr. bezeichnet die Position der präsentierten Aufgabe im Experiment. Zeit steht für die Mittelwerte der Lösungszeiten in Sekunden bei der jeweiligen Bedingung.
Die Steigungsparameter sind alle signifikant und haben ein negatives Vorzeichen; es ist also eine Abnahme der Lösungszeit mit zunehmender Übung im Umgang mit den Aufgaben - wie von Hypothese 1d vorhergesagt - nachweisbar. Aufgrund der Faktoren Bildschirmpräsentation oder Gruppe ergaben sich nur geringe Unterschiede in der Geschwindigkeit des Lerngewinns, was daran erkennbar ist, daß sich bei Berechnung einer Varianzanalyse keine signifikante Interaktion zwischen den Faktoren Bildschirmpräsentation und Aufgabendurchgang ergibt (siehe oben). Außerdem erbrachte ein Test auf signifikante Unterschiede in den Steigungsparametern (cf. Cohen und Cohen, 1983) des multiplikativen Modells keine signifikanten Differenzen (da hier jede einzelne Lösungszeit außer für die oben aufgeführte Varianzanalyse noch für zwei Regressionsanalysen verwendet wurde, muß für diese zusätzlichen Betrachtungen das Signifikanzniveau auf .017 adjustiert werden):
Die Lösungszeiten nehmen also im Verlauf des Experiments gemäß der Hypothese 1d bei allen Bedingungen ab; diese Abnahme erfolgt bei allen Bedingungen etwa gleich schnell. Betrachtet man die erste Ableitung der nach dem exponentiellen Modell gefitteten Gleichung, so zeigt sich, daß diese in der Grafik-Bedingung bis etwa zum neunten Durchgang unter der der Matrix-Bedingung liegt, später darüber (dieser Unterschied ist aber nur sehr schwach ausgeprägt). Dieser Sachverhalt könnte darauf hindeuten, daß in der Grafik-Bedingung der meiste Lernfortschritt früher stattfindet als in der Matrix-Bedingung.
Abbildung 3 zeigt, wie sich die Lösungszeiten innerhalb der Lösung einer Aufgabe verteilen: Es wird die Zeit, die zum Bearbeiten der ersten beiden Operatoren benötigt wird, mit der Zeit zur Ausführung der letzten beiden Operatoren verglichen.
Die Berechnung einer Varianzanalyse mit den Faktoren Position (erste vs. letzte Schritte) und Bildschirm für die Experimental-Gruppen zeigt, daß in der Matrix-Bedingung (zuerst 58, zuletzt 32 Sekunden) mehr Zeit benötigt wird als in der Grafik-Bedingung (zuerst 43, zuletzt 21 Sekunden); diese Differenz führt zu einem signifikantem Effekt des Faktors Bildschirmpräsentation (F(1; 38) = 9.661; p = .004) ebenso wie zu einem hochsignifikanten Effekt des Faktors Position (F(1; 38) = 39.263; p < .0005). Es tritt dagegen keine Interaktion zwischen diesen Faktoren auf (F(1; 38) = 0.336; p = .565). In beiden Bedingungen nimmt die Bearbeitungszeit etwa gleich ab.
In der Kontrollgruppe benötigen die Versuchspersonen in der Matrix-Bedingung (zuerst 28, zuletzt 29 Sekunden) wiederum länger als die Versuchspersonen in der Grafik-Bedingung (zuerst 20, zuletzt 20 Sekunden). Der Effekt der Bildschirmpräsentation ist also ebenfalls signifikant (F(1; 16) = 5.096; p = .038). Der Effekt der Position innerhalb der Aufgabe dagegen ist nicht signifikant (F(1; 16) = 0.276; p = .607); das selbe gilt für die Interaktion zwischen den beiden Faktoren Position und Bildschirmpräsentation (F(1; 16) = 0.389; p = .542). Die Bearbeitung der letzten beiden Schritte erfolgt also in der Kontrollbedingung nicht schneller als die Bearbeitung der ersten beiden Schritte.
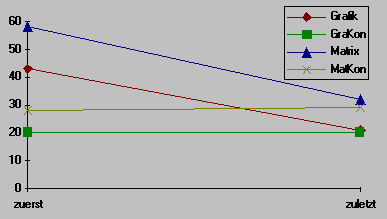
Abbildung 3: Die Verteilung der Lösungszeiten innerhalb der Aufgaben.
Die Werte der y-Achse sind die durchschnittlichen Zeiten in Sekunden, die für die ersten (zuerst) bzw. letzten (zuletzt) beiden Schritte einer Lösung benötigt wurden. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen.
Wird zur Überprüfung möglicher Interaktionen zusätzlich eine mehrfaktorielle Varianzanalyse (Bildschirmpräsentation x Gruppe x Position) berechnet, so erweist sich auch der Faktor Gruppe (Kontroll- oder Experimental-Gruppe) - trotz der erforderlichen Adjustierung des Signifikanzniveaus auf .025 - als sehr signifikant (F(1; 54) = 17.369; p < .0005). Die Faktoren Bildschirmpräsentation (F(1; 54) = 13.728; p < .0005) und Position (F(1; 54) = 36.370; p < .0005) sind ebenfalls sehr signifikant. Außerdem ist auch die Interaktion zwischen den Faktoren Gruppe und Bildschirmpräsentation sehr signifikant (F(1; 54) = 17.946; p < .0005).
Die Korrelation zwischen Lösungszeit und der Anzahl an Schritten
Es ergaben sich mittlere, signifikante (p < .001 in allen Fällen) Produkt-Moment-Korrelationskoeffizienten zwischen den beiden Variablen Lösungszeit und Anzahl der für die Lösung benötigten Schritte sowohl in der Experimental-Gruppe (rMatrix = .496; rGrafik = .408) als auch in der Kontroll-Gruppe (rMatrix = .39; rGrafik = .496). Die Lösungszeit hängt in beiden Gruppen nicht nur von der Anzahl der Schritte ab (die Varianzaufklärung beträgt in allen Fällen weniger als 25%).
Bezüglich des Lernfortschrittes, also der Steigung der Lernkurven, lassen sich zwischen den verschiedenen Bedingungen keine signifikanten Unterschiede nachweisen. Allerdings liegen die Lernparameter sowohl in der Experimental-Gruppe als auch in der Kontroll-Gruppe bei der grafischen Bildschirmpräsentation höher als bei der Präsentation als Matrix. Die etwas geringere Work-Load in der Grafik-Bedingung könnte also einen geringfügig schnelleren Lernfortschritt bewirken.
In die gleiche Richtung deuten auch die auf varianzanalytischem Wege erhaltenen Befunde: Bei den Experimental-Gruppen, bei denen eine hohe Work-Load herrscht, unterscheiden sich die Lösungszeiten der verschiedenen Bildschirmpräsentationen sehr signifikant, während die Unterschiede bei den Kontrollgruppen, die nur die optimale Strategie abarbeiten müssen, nicht signifikant bleiben (obwohl auch hier die Unterschiede zwischen den Mittelwerten in die gleiche Richtung weisen).
Die Verteilung der Lösungszeiten innerhalb der jeweiligen Aufgaben ist folgendermaßen begründbar: Die deutliche Abnahme der Bearbeitungszeit bei der Experimental-Gruppe liegt darin begründet, daß nach Ausführung einiger Schritte die Anzahl der Möglichkeiten bei der Auswahl weiterer Schritte deutlich reduziert ist. Bei den Kontroll-Gruppen findet eine solche Abnahme der Bearbeitungszeiten dagegen nicht statt. Dies deutet darauf hin, daß nicht versucht wurde, im Problemraum nach einem günstigen Zustand zu suchen (wobei der gegen Ende der Aufgabe deutlich verringerte Problemraum einen verringerten Zeitaufwand bedeuten würde); stattdessen wurde wohl eher der Instruktion gefolgt, nach der Strategie die Lösung zu erarbeiten, wobei hier kein geringerer Zeitaufwand gegen Ende der Aufgabe zu erwarten ist. Die signifikante Interaktion zwischen den Faktoren Gruppe (Experimental- und Kontroll-Gruppe) und Bildschirmpräsentation ist also darauf zurückzuführen, daß bei den Experimental-Gruppen die Zeit für die letzten beiden Schritte deutlich abnimmt, während sie bei den Kontrollgruppen gleich bleibt. Die Abnahme der Bearbeitungszeiten fällt bei der Experimental-Gruppe so deutlich aus, daß die letzten beiden Aktionen genauso schnell geplant und ausgeführt werden wie in der Kontrollgruppe. Bei ihnen scheint also keine Suche mehr zu erfolgen.
Die Korrelationen zwischen der Lösungszeit und der Anzahl der Schritte bewegen sich auf einem mittlerem Niveau, etwa zwischen .4 und .5. Die Lösungszeit hängt also zumindest teilweise von der Anzahl der Schritte ab. Dies läßt sich für die experimentellen Gruppen durch die Annahme einer Vorwärtssuche (forward search) erklären: Die Versuchsperson plant immer nur einen einzelnen Schritt und führt diesen dann aus. Erst nach dessen Ausführung wird der nächste Schritt überlegt. Deshalb hängt die Zeit, die zur Lösung einer Aufgabe benötigt wird, direkt mit der Anzahl der dabei ausgeführten Schritte zusammen. Bei den Kontroll-Gruppen muß nur eine bekannte Strategie Schritt für Schritt abgearbeitet werden. Für jeden einzelnen Schritt muß jeweils das nächstniedrige Kostenfeld gefunden werden, auf dem noch Einheiten zu vergeben sind. Die einzelnen Schritte sollten also etwa gleich lange Zeit benötigen (was sich auch bei der Verteilung der Lösungszeiten innerhalb einer einzelnen Aufgabe zeigt; siehe oben); somit ist auch bei diesen Gruppen der Zusammenhang zwischen Lösungszeit und Anzahl der Schritte erklärbar.
Dieser Zusammenhang ist jedoch nicht perfekt: Bei der Bearbeitung der Aufgaben können Fehler (Züge, die sich als ungünstig erweisen) und - wie sich bei der Bearbeitung der Aufgaben durch die Kontrollgruppen zeigte - Slips (Fehler bei der Ausführung eines geplanten Schrittes) auftreten, die es erforderlich machen, einen Schritt rückgängig zu machen; dazu ist wesentlich weniger Bedenkzeit erforderlich als zur Ausarbeitung eines neuen Schrittes. Ein anderer Grund für die Abschwächung des Zusammenhanges zwischen Lösungszeit und der Anzahl durchgeführter Schritte kann darin gesehen werden, daß sich der Problemraum mit der Anzahl der bereits ausgeführten Schritte drastisch verkleinert. Deshalb werden auch die letzten Schritte bei der Lösung einer Aufgabe deutlich schneller ausgeführt als die ersten (siehe oben). Entschließt sich die Versuchsperson zu Beginn der Bearbeitung einer Aufgabe zu einer Änderung der Teillösung, wird dafür wesentlich mehr Zeit benötigt, als wenn sie sich gegen Ende des Lösungsprozesses dazu entscheidet. Außerdem haben auch Faktoren wie die unterschiedliche Schwierigkeit der Aufgaben einen Einfluß auf die Lösungszeit.
Die beiden Bildschirmpräsentationen unterschieden sich nicht in ihrer Lösungsgüte, wie es von Hypothese 2a postuliert wurde. Dies konnte sowohl an der Häufigkeit optimaler Lösungen als auch an der jeweiligen Distanz zum Optimum gezeigt werden:
Für die Distanzen zum Optimum liegen jeweils nur relativ wenige von Null verschiedene Daten vor, da die Aufgaben zu einem hohen Anteil optimal gelöst wurden, d.h. die Distanzen zum Optimum Null waren: Auch in der Häufigkeit der optimalen Lösungen unterschieden sich weder die Experimental-Gruppen (Grafik: .73; Matrix: .73; t(38) = -0.051; p = .959) noch die Kontroll-Gruppen (Grafik-Kontrolle: .96; Matrix-Kontrolle: .94; t(16) = -0.489; p = .632) signifikant voneinander aufgrund der Bildschirmpräsentation.
Die tatsächlichen Distanzen zum Optimum wurden folgendermaßen normiert: Der jeweilige Kostenwert wurde durch die Kosten der optimalen Lösung dividiert und das Ergebnis wurde mit 100 multipliziert (siehe oben). Diese mittleren Distanzen sind in Abbildung 4 zu sehen.
Eine mehrfaktorielle Varianzanalyse mit der Distanz zum Optimum als abhängiger Variable ergab folgende Ergebnisse: Der Faktor Bildschirmpräsentation (Matrix oder Grafik) erreicht kein Signifikanzniveau (F(1; 54) = 0.048; p = .828). Die unterschiedliche Bildschirmpräsentation wirkt sich also auf die Distanz zum Optimum nicht aus.
Der Effekt des Faktors Gruppe (Experimental oder Kontrolle) ist signifikant (F(1; 54) = 6.043; p = .017). Es wirkt sich also deutlich auf die Distanz zum Optimum aus, ob der Versuchsperson bereits vor dem Experiment die optimale Lösungsstrategie gesagt wird.
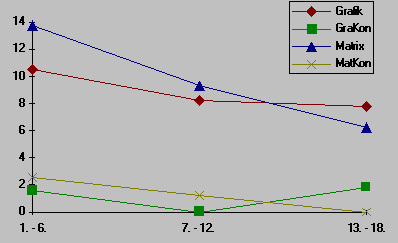
Abbildung 4: Die normierten Distanzen zum Optimum.
Die Werte der y-Achse sind die durchschnittlichen Abweichungen vom Optimum (normiert am Wert der optimalen Lösung). Der erste Wert auf der Abszisse ist der Mittelwert der 1. bis zur 6. Aufgabe, der zweite Wert ist der Mittelwert der 7. - 12. Aufgabe und der dritte Wert errechnet sich aus der 13. - 18. Aufgabe. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen.
Keine der Interaktionen zwischen diesen Faktoren erreicht auch nur annähernd Signifikanzniveau (in allen Fällen ist p > .4). Dies deutet insbesondere darauf hin, daß sich der Lernverlauf weder zwischen der Experimental-Gruppe und der Kontrollgruppe noch zwischen den Bildschirmpräsentationen signifikant unterscheidet.
Der Effekt des Faktors Aufgabenblock (1. - 3. Aufgabe sind der Block1; 4. - 6. Aufgabe sind der Block2 usw.) ist nicht signifikant (F(5; 270) = 1.762; p = .121). Es ist also auf diese Weise kein Lerneffekt nachweisbar; die Hypothese 2b, die annimmt, daß die Lösungen mit zunehmender Übung besser werden, muß also verworfen werden. Dieser Sachverhalt zeigt sich auch auf andere Weise: Der Versuch, die lineare Regression der Mittelwerte der Distanz zum Optimum auf die Aufgabenposition zu berechnen (wobei wegen der erneuten Betrachtung der Distanzen zum Optimum das Signifikanzniveau auf .025 adjustiert werden mußte) ergab für alle untersuchten Modelle nicht signifikante Steigungsparameter (für alle p > .19) und Determinationskoeffizienten unter .15; im Einzelnen ergaben sich folgende Gleichungen für die lineare Regression der normierten Distanz zum Optimum auf die Aufgabenposition:
|
Grafik (Experimental-Gruppe): |
y = 2.98 - 0.15 x; |
R^2 = 6.09%; |
|
Matrix (Experimental-Gruppe): |
y = 1.47 - 0.03 x; |
R^2 = 1.93%; |
|
Grafik (Kontroll-Gruppe): |
y = 0.10 - 0.001 x; |
R^2 = 0.12%; |
|
Matrix (Kontroll-Gruppe): |
y = 0.24 - 0.011 x; |
R^2 = 8.58%; |
Die Steigungsparameter waren zwar - wie zu erwarten - in allen Fällen negativ, aber recht niedrig.
Setzt man den Wert 0 für eine optimale Lösung und den Wert 1 für eine suboptimale Lösung und korreliert diesen Wert mit der für die Lösung der entsprechenden Aufgabe benötigten Zeit, so erhält man für alle Bedingungen, Grafik (r = .357), Matrix (r = .419), Grafik-Kontrolle (r = .492) und Matrix-Kontrolle (r = .404), signifikante (p jeweils < .001) und deutlich positive punkt-biseriale Korrelationen.
Insgesamt liegt die Wahrscheinlichkeit für eine optimale Lösung der Aufgaben auch in der Experimental-Gruppe sehr hoch: Fast drei Viertel aller Aufgaben wurden optimal gelöst. Diese überraschend hohe Wahrscheinlichkeit liegt wohl in der Struktur der Aufgaben begründet: Werden die ersten Züge günstig gewählt, bleiben für die übrigen Züge nur noch wenige Alternative übrig, aus denen die günstigsten offensichtlich häufig gefunden werden können. Auch die Anwendung anderer Strategien, z.B. der Angebotsstrategie (bei der versucht wird, das jeweils größte Angebot möglichst günstig zu vergeben; siehe Anhang G) oder der Bedarfsstrategie (bei der versucht wird, den jeweils höchsten Bedarf möglichst günstig zu befriedigen; siehe Anhang H) führt bei den verwendeten Aufgaben relativ häufig zur optimalen Lösung (Häufigkeit der optimalen Lösung bei Anwendung der Angebotsstrategie: .67; Häufigkeit bei Bedarfsstrategie: .5). Zwei wesentliche Merkmale der optimalen Strategie wurden auch unabhängig von der verwendeten Strategie von den Versuchspersonen angewandt und trugen dazu bei, daß so häufig die optimale Lösung gefunden wurde: Es wurde sehr häufig auf der jeweiligen Verbindung die maximale Anzahl an Einheiten vergeben (die durchschnittliche Häufigkeit in der Experimental-Bedingung betrug .85) und es wurde oft mit der billigsten Verbindung begonnen (die durchschnittliche Häufigkeit dieser Vorgehensweise in der Experimental-Bedingung betrug .60).
Die einzelnen Aufgaben wurden bei beiden Bildschirmpräsentationen etwa gleich oft optimal gelöst und auch die durchschnittliche Distanz zum Optimum unterscheidet sich nicht zwischen diesen Bedingungen. Die Aufgaben werden somit unter beiden Bedingungen etwa gleich gut gelöst (entsprechend Hypothese 2a). Der Grund könnte darin liegen, daß der Problemraum, der den Aufgaben zugrundeliegt, so groß ist, daß er unter keiner der beiden Bildschirm-Bedingungen durch Suche bewältigbar ist; es tritt ein sogenannter ceiling effect auf. Somit wird in beiden Bedingungen die Lösung jedesmal direkt aus der Aufgabenstellung ohne look-ahead erarbeitet, ohne daß dabei konkrete Strategien zur Anwendung kommen.
In den Kontrollgruppen ist die Wahrscheinlichkeit einer optimalen Lösung recht hoch (Matrix: .94; Grafik: .96). Dies ist auch zu erwarten, da ja die optimale Strategie bekannt war. Daß die Häufigkeit nicht bei 1 liegt, liegt daran, daß den Versuchspersonen bei der Abarbeitung der Strategie Fehler, sogenannte slips, unterlaufen sind. Im Gegensatz zu echten Fehlern, die auf falschen Vorstellungen oder Konzepten beruhen, handelt es sich bei slips um versehentlich falsch ausgeführte Aktionen (siehe z.B. Brown und VanLehn, 1980, S. 380).
Die niedrigen, nicht signifikanten Steigungsparameter der Regression der Mittelwerte der Distanz zum Optimum auf die Aufgabenposition deuten darauf hin, daß bezüglich der Lösungsgüte im Verlauf des Experiments keine nennenswerte Verbesserung eintrat; die Hypothese 2b muß deshalb verworfen werden.
Die Aufgaben, die optimal gelöst wurden, wurden auch schneller gelöst; andererseits wurde für die schlechter gelösten Aufgaben auch mehr Zeit benötigt, wie es von Hypothese 2c vorhergesagt wurde. Diese positive Korrelation zwischen Fehler und Lösungszeit, die dem bekannten speed-accuracy-trade-off zuwiderläuft, läßt sich am einfachsten damit begründen, daß die zu bearbeitenden Aufgaben empirisch unterschiedlich schwierig sind; dieser Sachverhalt wird unter dem Punkt "Die Variation in den Aufgaben" noch näher betrachtet werden. Dadurch kann es auftreten, daß für die Lösung einer schwierigen Aufgabe sowohl mehr Zeit benötigt wird als für die Lösung einer einfachen Aufgabe, als auch daß gleichzeitig eine größere Distanz zum Optimum auftritt. Eine weitere Begründung für die positive Korrelation zwischen Fehler und Lösungszeit kann darin gesehen werden, daß die Versuchspersonen bemerkten, wenn eine Lösung teuer zu werden drohte (dies zeigt sich in der positiven Korrelation zwischen geschätzter und tatsächlicher Distanz zum Optimum, die unten dargestellt wird); dies konnte möglicherweise dazu führen, daß sie Möglichkeiten suchten und überprüften, die Kosten doch noch zu minimieren; dazu war ein zusätzlicher Zeitaufwand nötig.
Außerdem kann noch folgende Überlegung zur Klärung der positiven Korrelation zwischen Fehler und Lösungszeit herangezogen werden: Wenn die optimale Strategie von der Versuchsperson erkannt wurde, dann sollte sie die Aufgaben sehr schnell bearbeiten können und außerdem eine optimale Lösung erzielen. Es liegt dann sowohl eine kurze Bearbeitungszeit als auch ein geringer Fehler vor.
Die minimale Anzahl an Schritten bei Anwendung der optimalen Strategie beträgt für die Aufgaben 1 bis 5 jeweils 5 Schritte, bei der Aufgabe 6 sind es nur 4 Schritte. Durchschnittlich beträgt die Mindestzahl an Schritten also 4.83.
Die durchschnittliche Anzahl der Schritte bis zur Lösung unterscheidet sich in der Experimental-Bedingung signifikant zwischen den beiden Bildschirmpräsentationen: Während in der Grafik-Bedingung durchschnittlich 6.19 Schritte ausgeführt werden müssen, sind es in der Matrix-Bedingung nur 5.53 (t(38) = -2.123; p = .040). Wie von Hypothese 3a postuliert, werden in der Grafik-Bedingung mehr Schritte getätigt.
Der Unterschied in der Anzahl der Schritte weist zwischen den Kontrollgruppen zwar in die gleiche Richtung (Grafik-Kontrolle: 5.37; Matrix-Kontrolle: 5.14), ist aber nicht so ausgeprägt, daß er signifikant wird (t (16) = 0.987; p = .339).
Die Anzahl der überflüssigen Schritte ergibt sich aus der Differenz zwischen der Anzahl der Felder der Lösungsmatrix, in denen ein Wert eingetragen wurde, und der Anzahl der Schritte bis zur Lösung. Es kann sich also nur um Schritte handeln, bei denen entweder ein Wert ausgebessert wurde oder eine Eingabe rückgängig gemacht wurde. Eine erhöhte Anzahl an Schritten wegen der Erzeugung einer suboptimalen Lösung bzw. der Anwendung einer suboptimalen Strategie wird auf diese Weise nicht erfaßt.
Von der Variable überflüssige Schritte ist nicht zu erwarten, daß sie normalverteilt ist, da sehr häufig der Wert Null auftritt und kein kleinerer Wert. Zur Überprüfung der Effekte von Aufgabendurchgang (um die wievielte Aufgabe es sich handelte), Bildschirmpräsentation und Gruppe wurde dennoch eine Varianzanalyse berechnet, da sich diese bei genügender Stichprobengröße als robust gegenüber Verletzungen der Normalverteilungsannahme erweist (siehe z.B. Bortz, 1985, S. 398). Bortz (1985, S. 346) schreibt dazu: "Abweichungen von der Normalität sind zu vernachlässigen, wenn die Populationsverteilungen schief sind."
Eine mehrfaktorielle Varianzanalyse mit Anzahl der überflüssigen Schritte als abhängiger Variable ergab folgende Ergebnisse: Der Effekt des Faktors Aufgabenblock (1. - 3. Aufgabe sind der Block1; 4. - 6. Aufgabe sind der Block2 usw.) ist nicht signifikant (F(5; 270) = 2.101; p = .066). Es ist also kein signifikanter Lerneffekt nachweisbar; die Hypothese 3c, die eine im Verlauf des Experiments abnehmende Häufigkeit überflüssiger Schritte vorhersagt, muß somit abgelehnt werden. Dieses Ergebnis liegt aber sehr nahe bei dem Signifikanzniveau von .05. Es lagen insgesamt nur sehr geringe Mittelwerte vor: (Block1: 0.822; Block2: 0.856; Block3: 0.948; Block4: 1.023; Block5: 0.661; Block6: 0.626). Bei den meisten Aufgaben wurde also durchschnittlich weniger als ein überflüssiger Schritt gemacht.
Der Faktor Bildschirmpräsentation (Matrix oder Grafik) erreicht Signifikanz (F(1; 54) = 0.5.218; p = .026). Die unterschiedliche Bildschirmpräsentation wirkt sich also auf die Anzahl der überflüssigen Schritte aus (siehe oben): die Hypothese 3a (mehr Schritte in der Grafik-Bedingung) kann also auch auf diese Weise gestützt werden.
Der Effekt des Faktors Gruppe (Experimental oder Kontrolle) ist signifikant (F(1; 54) = 6.382; p = .014). Es wirkt sich also deutlich auf die Anzahl der überflüssigen Schritte aus, ob der Versuchsperson bereits vor dem Experiment die optimale Lösungsstrategie gesagt wird (dies sollte auch nicht überraschen). Entsprechend den Vorhersagen von Hypothese 3b werden also in den Kontroll-Gruppen weniger Schritte benötigt.
Keine der Interaktionen zwischen diesen Faktoren erreicht auch nur annähernd Signifikanzniveau (in allen Fällen ist p > .33). Dies deutet insbesondere darauf hin, daß sich der Lernverlauf weder zwischen der Experimental-Gruppe und der Kontrollgruppe noch zwischen den Bildschirmpräsentationen signifikant unterscheidet.
Betrachtet man den Verlauf der Anzahl der überflüssigen Schritte (Abbildung 5), fällt auf, daß diese Anzahl - von gewissen, wahrscheinlich zufallsbedingten Schwankungen abgesehen - relativ konstant zu bleiben scheint, was wiederum die Hypothese 3c widerlegt. Auch in bezug auf die Anzahl der überflüssigen Schritte kann man also wieder sagen, daß im weiteren Verlauf des Experiments keine Verbesserung der Lösungsgüte (diesmal bezüglich der Effizienz der Lösungssuche) stattfindet.
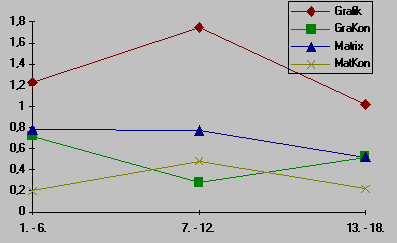
Abbildung 5: Die durchschnittliche Anzahl überflüssiger Schritte.
Die Werte der y-Achse geben die durchschnittliche Anzahl der überflüssigen Schritte an. Der erste Wert auf der Abszisse ist der Mittelwert der 1. bis zur 6. Aufgabe, der zweite Wert ist der Mittelwert der 7. - 12. Aufgabe und der dritte Wert errechnet sich aus der 13. - 18. Aufgabe. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen.
Die in der Grafik-Bedingung höher liegende Anzahl an Schritten, insbesondere an überflüssigen Schritten, läßt sich damit begründen, daß die Ausführung eines Schrittes in der Matrix-Bedingung mit einem höherem Aufwand verbunden ist; deshalb wird die Wirkung eines Schrittes dort möglicherweise vor dessen Ausführung genauer mental evaluiert, was sich eventuell in einer größeren Suchtiefe oder in einer geringeren Situationsabstraktion, d.h. dem detaillierterem Betrachten der potentiell resultierenden Situation, auswirken könnte. In der Grafik-Bedingung dagegen bereitet die Ausführung - und somit auch das Rückgängig-Machen - eines Operators einen relativ geringen Aufwand. Dieser Tatbestand kann die Versuchsperson dazu verleiten, daß sie einen Schritt einfach ausführt und ihn, wenn sich erweisen sollte, daß er ungünstig war, einfach wieder abändert. Die (vorläufige) Ausführung eines Schrittes bietet der Versuchsperson den Vorteil, daß der gesamte daraus resultierende Zustand am Bildschirm angezeigt wird. Soll der nächste Zustand dagegen mental erzeugt werden, müssen zwei Subtraktionen (beim zur Verfügung stehenden Angebot und Bedarf) durchgeführt werden und ihr Ergebnis muß im Arbeitsgedächtnis gehalten werden.
Die Tatsache, daß die Anzahl der überflüssigen Schritte im Verlauf des Experiments nicht abnimmt, kann durch das Ausbleiben des Erwerbs einer Lösungsstrategie erklärt werden: Dieses führt dazu, daß jede Lösung neu erstellt werden muß, wobei eine ungünstige Teillösung Ausbesserungen (und somit überflüssigen Schritten) notwendig machen kann.
Die subjektiven Distanzen zum Optimum, die auf die gleiche Art normiert wurden wie die tatsächlichen Distanzen zum Optimum, unterschieden sich weder in den Experimental-Bedingungen (Grafik: 2.84; Matrix: 3.60; t(38) = 0.624; p = .536) noch in den Kontroll-Bedingungen (Grafik-Kontrolle: 0.29; Matrix-Kontrolle: 0.20; t(16) = 0.318; p = .755) signifikant aufgrund der Bildschirmpräsentation; die Versuchspersonen hielten ihre Lösungen in beiden Bedingungen also für gleich gut. Die Unterschiede zwischen den Experimental- und den Kontroll-Gruppen waren dagegen außerordentlich stark ausgeprägt: Die subjektive Distanz zum Optimum wurde in den Experimental-Gruppen etwa 10 mal höher eingeschätzt als in den Kontroll-Gruppen; dies entspricht den Vorhersagen der Hypothese 4a, daß die Lösungen in den Kontroll-Gruppen für besser gehalten werden.
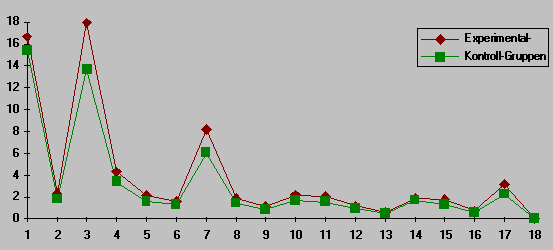
Abbildung 6:
Auf der Ordinate ist die durchschnittliche Differenz zwischen subjektiver und objektiver Distanz (normiert) zum Optimum in den Experimental- und Kontrollgruppen aufgetragen; auf der Abszisse stehen die Positionen der Aufgaben während des Experiments. Da sich die beiden Bildschirmpräsentationen nicht signifikant unterscheiden, wurden die Mittelwerte verwendet.
Die Differenz zwischen der subjektiven Distanz zum Optimum und der tatsächlichen Distanz zum Optimum, also die Ungenauigkeit der Vorhersage der Versuchsperson bezüglich der Abweichung vom Optimum nimmt sowohl bei den Experimental-Gruppen als auch bei den Kontroll-Gruppen (siehe Abbildung 6) während der ersten neun Lerndurchgänge stark ab und bleibt dann etwa konstant. Die Berechnung der multiplikativen Regression der Differenz zwischen subjektiver und tatsächlicher Distanz zum Optimum auf die Aufgabenposition ergab für alle Bedingungen signifikant negative Steigungsparameter:
|
Experimentelle Grafik-Bedingung: |
y = exp(3.18 * x-1.39); |
R^2 = 31.00%; |
|
Experimentelle Matrix-Bedingung: |
y = exp(3.02 * x-1.20); |
R^2 = 36.18%; |
|
Kontroll-Grafik-Bedingung: |
y = exp(2.59 * x-1.18); |
R^2 = 39.80%; |
|
Kontroll-Matrix-Bedingung: |
y = exp(2.87 * x-1.20); |
R^2 = 37.36%. |
Die Schätzungen werden also, wie von Hypothese 4b vorhergesagt, besser.
Zur Berechnung der Korrelation zwischen der tatsächlichen und der geschätzten Distanz zum Optimum, einem Maß für die Genauigkeit der Schätzungen der Versuchspersonen, wurde die Produkt-Moment-Korrelation zwischen diesen beiden Variablen berechnet. Die in allen Fällen signifikante (p < .001) Korrelation zwischen der Distanz zum Optimum und der geschätzten Distanz zum Optimum liegt in den Experimental-Gruppen (rMatrix = .48; rGrafik = .532) deutlich niedriger als in den Kontroll-Gruppen (rMatrix = .911; rGrafik = .908).
Der Anteil der Aufgaben, bei denen die Versuchsperson glaubt, sie seien optimal gelöst, unterscheidet sich in der Experimental-Gruppe zwischen der Matrix-Bedingung (Häufigkeit: .372) und der Grafik-Bedingung (Häufigkeit: .525) nicht signifikant (t(38) = 1.4344; p = .1596). Auch in der Kontrollgruppe unterscheiden sich die Matrix-Bedingung (Häufigkeit: .948) und die Grafik-Bedingung (Häufigkeit: .96) nicht signifikant (t(38) = 0.4809; p = .637). Die Unterschiede zwischen der Experimental-Gruppe und der Kontrollgruppe sind dagegen sowohl bei der Matrix-Bedingung (t(27) = -5.257; p < .0005) als auch bei der Grafik-Bedingung (t(27) = -3.667; p = .0011) signifikant.
Es kann nicht davon ausgegangen werden, daß die subjektiven Einschätzungen der Aufgabenschwierigkeit (3.0 entspricht "mittel") Intervallskalenniveau besitzen; zum Vergleich der Gruppenmittelwerte wurde deshalb der U-Test von Mann-Whitney verwendet. Sie unterschieden sich ebenfalls weder in den Experimental-Bedingungen (Grafik: 2.98; Matrix: 2.91; Z = 0.434; p = .664) noch in den Kontroll-Bedingungen (Grafik-Kontrolle: 2.50; Matrix-Kontrolle: 2.54; Z = .01; p = .999). Zwischen den Experimental-Gruppen und den Kontroll-Gruppen zeigte sich aber doch ein signifikanter Unterschied: Wenn die optimale Strategie der Versuchsperson vor dem Experiment genannt wird, erscheinen ihr die Aufgaben leichter; dieser Unterschied zeigte sich sowohl bei den Grafik-Gruppen (Z = 1.961; p = .049) als auch bei den Matrix-Gruppen (Z = 2.031; p = .042). Dies deutet darauf hin, daß die Anwendung der Strategie nicht sonderlich schwer fällt. Dabei kann es sich aber auch um einen Effekt der Vorgehensweise beim Experiment handeln: Die Versuchspersonen sollten die Schwierigkeit der Bearbeitung der ersten Aufgabe als Standard für die Beurteilung der Schwierigkeit der übrigen Aufgaben verwenden. In den Kontrollgruppen wurde die optimale Lösungsstrategie den Versuchspersonen aber erst nach der ersten Aufgabe erklärt. Deshalb können die restlichen Aufgaben vergleichsweise leicht erscheinen.
Es zeigten sich einige Faktoren, mit denen die subjektive Aufgabenschwierigkeit zusammenzuhängen scheint. Bei der Berechnung der entsprechenden Korrelationen wurde auf eine a -Adjustierung des Signifikanzniveaus verzichtet, da es sich bei der vorliegenden Arbeit um eine eher explorative Untersuchung handelt, bei der möglicherweise tatsächlich vorhandene Zusammenhänge nicht durch Wahl eines zu konservativen Signifikanzniveaus unentdeckt bleiben sollten. Da die Variable subjektive Aufgabenschwierigkeit kein Intervallskalenniveau besitzt, erfolgte jeweils die Berechnung der Rang-Korrelationen nach Spearman. Folgende Korrelationen zwischen der subjektiven Schwierigkeit aller einzelnen Aufgaben und weiteren Variablen wurden berechnet:
Bezüglich der Genauigkeit der Schätzung des Abstandes zum Optimum läßt sich ein gewisser schwacher Lerneffekt feststellen, der sich aber nicht signifikant auswirkt. In der Kontrollgruppe sind die Schätzungen dabei genauer. Dies ist aber nicht überraschend, da in der Kontrollgruppe meist die optimale Lösung erzielt wird und diese auch erwartet wird; in diesen Fällen entspricht die Schätzung genau dem tatsächlichen Wert, und somit kommt es natürlich zu einer geringeren durchschnittlichen Abweichung zwischen geschätzter und tatsächlicher Differenz zum Optimum. Der signifikant höhere Anteil an Versuchspersonen in der Kontrollgruppe gegenüber der Experimental-Gruppe, die glauben, eine Aufgabe optimal gelöst zu haben, liegt wohl daran, daß sich die Versuchspersonen in den Kontrollgruppen wegen der Kenntnis der optimalen Strategie relativ sicher sein konnten, die optimale Lösung erzeugt zu haben, während dies in den Experimental-Gruppen nicht der Fall war. Die relativ geringen Häufigkeiten des Einschätzens einer Lösung als optimal in den Experimental-Gruppen deuten darauf hin, daß dort die Versuchspersonen nicht von der Optimalität ihrer Vorgehensweise überzeugt waren. Sollten sie tatsächlich eine Strategie befolgt haben, hielten sie diese nicht immer für die optimale.
Die subjektive Aufgabenschwierigkeit liegt unter allen Bedingungen unter dem Standardreiz. Dies deutet darauf hin, daß die Aufgaben mit zunehmender Erfahrung bei ihrer Lösung leichter erscheinen. Der nicht signifikante Effekt des Faktors Bildschirm-Präsentation kann dadurch erklärt werden, daß die Versuchspersonen nach der Bearbeitung der ersten Aufgabe instruiert worden waren, diese als Standardreiz für die Beurteilung der Schwierigkeit zu verwenden. Somit wurden eventuelle Unterschiede im Mittelwert der subjektiven Aufgabenschwierigkeit ausgeglichen.
Die deutliche negative Korrelation zwischen subjektiver Aufgabenschwierigkeit und der empirischen Wahrscheinlichkeit, mit der die entsprechende Aufgabe optimal gelöst wurde, zeigt, daß empirisch schwierige Aufgaben auch subjektiv schwieriger erscheinen. Dies wird auch durch die Korrelation zwischen der subjektiven Aufgabenschwierigkeit und der Distanz zum Optimum bei der Lösung der entsprechenden Aufgabe nahegelegt.
Die Korrelation zwischen subjektiver Schwierigkeit und der geschätzten Distanz zum Optimum liegt erstaunlich niedrig; die Schwierigkeit einer Aufgabe wird demnach nicht nur danach beurteilt, wie gut die Versuchsperson bei ihrer Lösung gewesen zu sein glaubt. Die (nur) mittlere Korrelation zwischen der Aufgabenschwierigkeit und der Lösungszeit deutet darauf hin, daß sich die Versuchsperson bei der Beurteilung der Aufgabenschwierigkeit nicht nur daran orientiert, wie viel Zeit sie für die gerade bearbeitete Aufgabe benötigt hat. Die Anzahl der zur Lösung benötigten Schritte hat keinen Einfluß auf die Beurteilung der Aufgabenschwierigkeit; die Versuchspersonen orientieren sich also bei der Beurteilung der Aufgabenschwierigkeit nicht an der für die Lösung benötigten Anzahl von Schritten.
Die Nullkorrelation zwischen der subjektiven Aufgabenschwierigkeit der Größe des Problemraum bzw. des Lösungsraums widerlegt die Vermutung, daß die Schwierigkeit einer Aufgabe nach dem Aufwand für die Suche im vollständigen Problemraum abhängt.
4.6. Die Variationen in den Aufgaben
Nährer (1982) weist darauf hin, daß der Zeitbedarf für die Lösung einer Aufgabe unter Umständen nicht nur von der angewandten Strategie abhängt, sondern daß es zu einer Interaktion zwischen Itemkomplexität und Bearbeitungsstrategie kommen kann: Bei den von ihm verwendeten Aufgaben - einer Übersetzung des logischen Aussagenkalküls in einen äquivalenten graphischen - wurde für die Lösung der Aufgaben bei einfachen Items und Anwendung einer einfachen Strategie weniger Zeit benötigt als bei Anwendung einer komplexen Strategie (die auch irrelevante Merkmale betrachtete). Komplexe Aufgaben hingegen wurden mit der komplexen Strategie schneller gelöst.
Siegler (1987) warnt davor, über verschiedene Strategien hinweg Mittelwerte zu bilden, da es ansonsten zu Verzerrungen in den Ergebnissen kommen könnte: Es ergibt sich eine wesentlich bessere Passung, wenn die Daten nach verschiedenen Strategien getrennt gefittet werden. Zur Erfassung der Strategien könnten Verbalprotokolle und Aufgabenanalysen verwendet werden.
Bei der Auswertung des hier beschriebenen Experiments konnte nicht zwischen den einzelnen Aufgaben unterschieden werden, die mit unterschiedlichen Strategien gelöst wurden, da diese Strategien nicht genau identifizierbar waren. Deshalb ist bei der Interpretation des Zusammenhangs zwischen der Variation in den Aufgaben und der Lösungszeit Vorsicht geboten.
Der Effekt der verschiedenen Aufgaben, gemittelt über ihre isomorphen Varianten ist bei den Experimental-Gruppen in bezug auf die Lösungszeit hoch signifikant (F(5; 190) = 10.663; p < .0005); die Mittelwerte der Lösungszeiten und deren Standardabweichungen sind für die einzelnen Aufgaben in Tabelle 3 aufgeführt. Es zeigt sich, daß für Aufgaben mit unterschiedlicher Struktur (verschiedenem zugrundeliegenden Problemraum), wie von Hypothese 6b vorhergesagt, unterschiedlich lange Lösungszeiten benötigt werden; die Aufgaben scheinen also unterschiedlich schwer zu sein.
|
|
Mittelwert |
SD |
Mittelwert. |
SD |
Mittelwert |
SD |
|
t20_1* |
95,5 |
32,1 |
134,8 |
54,1 |
115,2 |
48,2 |
|
t20_2* |
94,6 |
33,8 |
149,5 |
67,1 |
122,1 |
59,3 |
|
t20_3* |
100,3 |
34,8 |
140,5 |
56,3 |
120,4 |
50,5 |
|
t20_4* |
101,7 |
42,1 |
139,6 |
52,9 |
120,7 |
51,0 |
|
t20_5* |
119,7 |
62,6 |
160,3 |
70,8 |
140,0 |
69,1 |
|
t20_6* |
82,8 |
22,2 |
104,4 |
36,2 |
93,6 |
31,6 |
Tabelle 3: Mittelwerte und Standardabweichung (SD) der Lösungszeiten (in Sekunden) der Aufgaben bei den Experimental-Gruppen
, gemittelt über die isomorphen Varianten und getrennt für die Präsentationsbedingungen graphisch (n = 20) und Matrix (n = 20). Der Effekt der Bildschirmpräsentation (F(1; 38) = 8.747; p < .0005) ist sehr signifikant; der Effekt der Aufgaben (F(5; 190) = 10.663; p < .005) ist sehr signifikant, die Interaktion zwischen diesen Faktoren ist nicht signifikant (F(5; 190) = 1.346; p = .247).
Dabei fällt auf, daß für die Aufgabe6, bei der zur optimalen Lösung nur 4 Schritte nötig sind, besonders schnell gelöst wird, während die Aufgabe5 besonders lange Lösungszeiten benötigt. Die Interaktion des Effektes der Aufgaben mit der Bildschirmpräsentation ist dagegen nicht signifikant (F(5; 190) = 1.346; p = .247).
In der Kontrollgruppe, deren Ergebnisse in Tabelle 4 dargestellt sind, wirkt sich der Effekt der verschiedenen Aufgaben dagegen nicht signifikant aus (F(5; 80) = 1.875; p = .108); Hypothese 6c, die für die Kontroll-Gruppen keine Unterschiede in den Lösungszeiten aufgrund der Aufgabenstruktur vorhersagt, kann also beibehalten werden.
|
|
Mittelwert |
SD |
Mittelwert. |
SD |
Mittelwert |
SD |
|
t20_1* |
52,5 |
16,1 |
81,6 |
44,5 |
67,0 |
35,7 |
|
t20_2* |
60,7 |
22,3 |
78,4 |
29,2 |
69,5 |
26,8 |
|
t20_3* |
63,4 |
13,0 |
83,5 |
34,3 |
73,4 |
27,2 |
|
t20_4* |
60,7 |
16,2 |
75,4 |
26,4 |
68,1 |
22,6 |
|
t20_5* |
65,5 |
14,8 |
84,3 |
41,9 |
74,9 |
32,0 |
|
t20_6* |
54,9 |
13,1 |
67,0 |
22,5 |
60,9 |
18,9 |
Die isomorphen Varianten der Aufgaben
Der Effekt der verschiedenen isomorphen Varianten einer Aufgabe (klein-eng, groß-eng und groß-weit) war in der Experimental-Gruppe knapp nicht signifikant (F(2; 76) = 2.843; p = .064); die entsprechenden Ergebnisse sind Tabelle 5 zu entnehmen. Die Hypothese 6a, die Unterschiede in den Lösungszeiten wegen der Kostenhöhe und dem Kostenabstand vorhersagt, muß also verworfen werden. Betrachtet man die Gruppenmittelwerte jedoch genauer, so fällt auf, daß sich die Bedingung klein-eng (Mittelwert: 111.8) von den beiden anderen Bedingungen groß-eng (Mittelwert: 122.6) und groß-weit (Mittelwert: 121.5) unterscheidet. Werden nur relativ kleine Zahlen verwendet, scheint die Lösung der Aufgaben beschleunigt zu werden.
|
|
Mittelwert graphisch |
SD graphisch |
Mittelwert Matrix |
SD Matrix |
Mittelwert gesamt |
SD gesamt |
|
klein - eng |
93,7 |
29,7 |
129,9 |
46,9 |
111,8 |
42,9 |
|
groß - eng |
102,2 |
38,3 |
143,1 |
54,6 |
122,6 |
50,9 |
|
groß - weit |
101,4 |
38,7 |
141,6 |
58,8 |
121,5 |
53,2 |
Tabelle 5: Die Mittelwerte der Lösungszeiten (in Sekunden) bei verschiedenen isomorphen Aufgabenvarianten bei den Experimental-Gruppen
; getrennt für die graphische Bedingung (n = 20) und für die Matrix-Bedingung (n = 20) und gemittelt über beide. SD steht für Standardabweichung. Der Effekt der Bildschirmpräsentation (F(1; 38) = 8.747; p < .005) ist sehr signifikant; der Effekt des Aufgabentyps (F(2; 76) = 2.843; p = .064) ist knapp nicht signifikant. Die Interaktion zwischen diesen Faktoren ist nicht signifikant (F(2, 76) = 0.124; p = .883).
In den Kontrollgruppen, deren Kennwerte in Tabelle 6 zu sehen sind, war der Effekt der isomorphen Varianten der Aufgaben dagegen deutlicher nicht signifikant (F(2; 32) = 0.347; p = .709). Bei der reinen Abarbeitung der Aufgaben unterscheiden sich also die Bedingungen klein-eng (Mittelwert: 67.4), groß-eng (Mittelwert: 69.5) und groß-weit (Mittelwert: 70.1) kaum.
|
|
Mittelwert graphisch |
SD graphisch |
Mittelwert Matrix |
SD Matrix |
Mittelwert gesamt |
SD gesamt |
|
klein - eng |
54,6 |
14,3 |
80,1 |
32,3 |
67,4 |
27,6 |
|
groß - eng |
61,4 |
11,9 |
77,6 |
32,0 |
69,5 |
24,8 |
|
groß - weit |
62,8 |
17,6 |
77,4 |
27,7 |
70,1 |
23,7 |
Tabelle 6: Die Mittelwerte der Lösungszeiten (in Sekunden) bei verschiedenen isomorphen Aufgabenvarianten bei den Kontrollgruppen
; getrennt für die graphische Bedingung (n = 9) und für die Matrix-Bedingung (n = 9) und gemittelt über beide. SD steht für Standardabweichung. Weder die Effekte des Faktors Bildschirmpräsentation (F(1; 16) = 3.094; p = .098) noch des Faktors Aufgabentyp (F(2; 32) = 0.347; p = .709) sind signifikant. Die Interaktion zwischen diesen Faktoren ist ebenfalls nicht signifikant (F(2,32) = 1.474; p = .244).
Die Interaktion zwischen der Bildschirmpräsentation und dem Aufgabentyp ist weder in der Experimental-Bedingung (F(2; 76) = 0.124; p = .883) noch in der Kontroll-Bedingung (F(2; 32) = 1.474; p = .244) signifikant.
Die einzelnen Aufgaben sind, wie bereits oben bemerkt, in der Experimental-Gruppe unterschiedlich schwierig: Es treten signifikante Unterschiede in der zur ihrer Lösung benötigten Zeit auf. Dazu ist zu bemerken, daß diejenige Aufgabe, die sowohl bei den Experimental-Gruppen als auch bei den Kontroll-Gruppen am schnellsten gelöst wurde, auch diejenige ist, zu deren optimaler Lösung nur 4 Schritte nötig sind (bei allen anderen Aufgaben sind es 5 Schritte).
In der Kontrollgruppe wirkt sich dagegen die Struktur der Aufgabe nicht signifikant auf die entsprechende Lösungszeit aus. Die reine Abarbeitung der Strategie scheint also von der Struktur der konkret vorgegebenen Aufgabe nicht zu stark abzuhängen.
Die beinahe signifikante Wirkung der isomorphen Aufgabenvariation in der Experimental-Bedingung deutet darauf hin, daß die Versuchspersonen möglicherweise bei der Suche nach der Lösung Teilergebnisse berechneten; dies würde erklären, daß die Variation klein-eng, bei der nur niedrige Zahlen vorkommen, schneller bearbeitet wird als die Variationen, bei denen größere Zahlen Verwendung finden. Daß es sich nicht nur um einen Effekt der unterschiedlichen Schwierigkeit der Rangreihenbildung handelt, kann daran gesehen werden, daß sich die Variationen groß-eng und groß-weit kaum in ihrer Lösungszeit voneinander unterscheiden. Es ist aber zu erwarten, daß die Bildung einer Rangreihe bei der Variation groß-weit leichter (und somit schneller) gehen müßte als bei der Variation groß-eng, weil die größeren Anstände zwischen den Zahlen die Größenvergleiche erleichtern.
Die Unterschiede zwischen der Variation klein-eng und den beiden anderen Variationen sind in der Kontrollgruppe geringer; dort wird ja so vorgegangen, daß eine Rangreihe gebildet wird (und die Versuchspersonen wurden explizit instruiert, nicht zu rechnen). Die Variationen der Aufgaben zeigen bei den unterschiedlichen Bildschirmpräsentationen keine signifikante Wirkung (die Interaktion dieser beiden Faktoren ist nicht signifikant).
4.7. Die Anwendung von Strategien
Es ließen sich mehrere von den Versuchspersonen angewandte Heuristiken nachweisen, die dazu beitrugen, den ansonsten kaum bewältigbaren Problemraum drastisch zu verkleinern. Am wichtigsten erscheint, daß sehr häufig auf der gerade bearbeiteten Verbindung maximal viel vergeben wurde. Dies geschah in der Matrix-Bedingung (mittlere Häufigkeit .935) signifikant öfter als in der Grafik-Bedingung (mittlere Häufigkeit: .77; t(38) = 5.475; p < .0005). Der Grund kann darin liegen, daß die Versuchspersonen in beiden Bedingungen jeweils maximal viel vergeben wollten, daß aber in der Matrix-Bedingung der eingegebene Wert wegen der unterschiedlichen Vorgehensweise bei der Eingabe genauer überlegt werden konnte. Darauf deutet auch der ebenfalls signifikante Unterschied (t(16) = 3.447; p = .0034) zwischen der Grafik-Kontrollgruppe (mittlere Häufigkeit: .913) und der Matrix-Kontrollgruppe (mittlere Häufigkeit: .981) hin. Hätten sich die Versuchspersonen in der Kontrollgruppe genau an die Instruktionen gehalten, müßte die Häufigkeit bei beiden Gruppen 1.0 betragen.
Eine weitere erfolgreiche Heuristik, die ebenfalls Teil der optimalen Strategie ist, besteht darin, mit der billigsten Verbindung zu beginnen. Dies geschah in der experimentellen Grafik-Bedingung (mittlere Häufigkeit: .636) etwa genauso oft wie in der Matrix-Bedingung (mittlere Häufigkeit: .561); der Unterschied ist nicht statistisch signifikant (t(38) = 0.906; p = .370). Die mittlere Häufigkeit des Beginnens mit dem billigsten Feld betrug in den Kontrollgruppen .889 (Grafik) bzw. .864 (Matrix); dieser Unterschied ist ebenfalls nicht signifikant (t(16) = 0.644; p = .528). Auch dies ist ein Beleg dafür, daß dort die optimale Strategie nicht immer befolgt wurde.
Die hier genannten Heuristiken tragen dazu bei, die Komplexität der gestellten Aufgaben dadurch zu reduzieren, daß bei der Lösung der einzelnen Aufgaben weniger Elemente der Aufgabenstellung betrachtet werden müssen. Diese Heuristiken bewirken einerseits, daß die Lösungen der Aufgaben relativ gut sind und daß andererseits weniger Zeit zur Lösung der Aufgaben benötigt wird. Leplat (1988, S. 113) meint in diesem Zusammenhang: "The development of skill may be viewed as the elaboration of a cognitive complexity reducing mechanism."
Ob eine Aufgabe nach der optimalen Strategie gelöst wurde, kann auf zwei Arten festgestellt werden:
Man bestimmt für jedes Feld der Kostenmatrix die Rangposition der relativen Kosten; dies bedeutet, daß der billigsten Verbindung der Wert 1 zugewiesen wird, der zweitbilligsten Verbindung der Wert 2 usw. Beträgt die Rang-Korrelation nach Spearman zwischen Position in der Zugfolge des Probanden und diesen relativen Kosten des angewählten Feldes 1 (bzw. liegt sie über .99, da Rechenungenauigkeiten auftreten können), so wurde bei der Lösung der entsprechenden Aufgabe nach der optimalen Strategie vorgegangen; liegt der Wert nahe bei 1; wurde prinzipiell entsprechend der Strategie vorgegangen, d.h. es wurde global versucht, von den billigen Verbindungen zu den teueren weiter zu arbeiten. Ein möglicher Grund, daß dies nicht ganz genau geschah, kann darin bestehen, daß Fehler - sogenannte slips - bei der Anwendung der Strategie auftreten können. Zusätzliche Schritte, bei denen ein Feld entsprechend der Rangreihe angewählt wurde, auf dem nichts zu vergeben ist, wurde, fallen bei dieser Art der Identifikation nicht ins Gewicht.
Die andere Möglichkeit der Identifikation besteht in einem Match von 1 zwischen vorhergesagter und tatsächlicher Operatorfolge: Dazu wurde der von Card, Moran und Newell (1983, S. 190f) vorgestellte Algorithmus implementiert. Dieser Algorithmus "takes as input predicted and observed sequences and returns the percentage of matches and new versions of the input sequences resulting from the addition of dummy operators" (Card et al., 1983, S. 190). Ein einzelner Operator besteht dabei in der Wahl einer bestimmten Verbindung von einem Ausgangsort zu einem Zielort.
Beide hier vorgestellten Möglichkeiten identifizieren die Anwendung der Strategie aufgrund der Reihenfolge, in der die Verbindungen bearbeitet werden. Dabei wird nicht berücksichtigt, wie viele Einheiten jeweils vergeben werden. Aus folgenden Gründen kann man aber dennoch davon ausgehen, daß auf diese Weise die Anwendung der Strategie erfaßt wird: Bei Anwendung der Strategie müßte auf jeder Verbindung maximal viel vergeben werden. Dies war - wie sich empirisch zeigte - auch sehr häufig der Fall. Wurde auf einer Verbindung nicht maximal viel vergeben, so müssen später auf einer zusätzlichen Verbindung Einheiten vergeben werden; diese zusätzliche Aktion zeigt sich in einer geringeren Korrelation zu den relativen Kosten bzw. in einem geringeren Match mit der vorhergesagten Operatorfolge. Wird also nicht nach der Strategie vorgegangen, so fallen die Kennwerte niedriger aus.
Aus den Verbalprotokollen konnten noch zwei weitere Strategien identifiziert werden, die die Versuchspersonen nennen konnten: Die Angebots-Strategie (nach der die Einheiten von dem Ort, der jeweils das meiste Angebot besaß, möglichst billig vergeben werden sollten; siehe Anhang G) und die Bedarfs-Strategie (nach der die Einheiten zu dem Ort, der jeweils den höchsten Bedarf benötigte, möglichst billig transportiert werden sollten; siehe Anhang H). Die Anwendung dieser beiden Strategien wurde wiederum durch den Match zwischen der durch die jeweilige Strategie vorhergesagten Operatorfolge und der tatsächlich aufgetretenen Operatorsequenz identifiziert. Die Häufigkeit der Anwendung der Angebots- und der Bedarfsstrategie schwankt sowohl bei der Grafik- als auch bei der Matrix-Bedingung zwischen .02 und .03. Diese Häufigkeiten sind zu niedrig, um sinnvoll über den Verlauf der Anwendung dieser Strategien mit zunehmender Übung sprechen zu können.
|
VP1g |
ooo*************** |
VP5m |
oo**oo*ooo*o*ooooo |
|
VP5g |
oo*oooo*****oooooo |
VP7m |
***o**o*oo*o*****o |
|
VP6g |
***ooooo*oooooo*oo |
VP9m |
o*o**********o*o*o |
|
VP7g |
o*o*oooo**o*oo*ooo |
VP10m |
oooooo*ooooo*o**** |
|
VP8g |
*o****o**o*o*oo*** |
VP11m |
oooo************** |
|
VP9g |
o*ooooo**ooooooooo |
VP13m |
ooo*o************* |
|
VP10g |
ooooooooooo**o*oo* |
VP15m |
**o*o*o*o*o***o*o* |
|
VP15g |
*o**o**o*oo******* |
VP20m |
**ooooo**o*ooo*o** |
|
VP17g |
ooooo*o*oo*o*o***o |
|
|
|
VP18g |
***oooooo*o***o**o |
|
|
Tabelle 7: Die Anwendung der optimalen Strategie.
Es sind alle Versuchspersonen aufgezeichnet, die die optimale Strategie mindestens drei Mal angewandt haben; "*" bedeutet, daß im entsprechenden Durchgang nach der Strategie vorgegangen wurde (Match > .75), "o" bedeutet, daß dies nicht der Fall war. Die Position in der Zeichenkette entspricht dem Durchgang innerhalb des Experiments. Ein g am Ende der Bezeichnung einer Versuchsperson bedeutet, daß diese in der experimentellen Grafik-Bedingung am Experiment teilnahm, ein m steht für die experimentelle Matrix-Bedingung.
Bildschirmpräsentation und Anwendung der optimalen Strategie
Wird die Anzahl der nach der optimalen Strategie gelösten Aufgaben durch einen Match von 1 festgelegt, dann unterscheidet sich die Häufigkeit der nach der Strategie gelösten Aufgaben unter den verschiedenen Bildschirmpräsentationen weder in der Experimental-Bedingung (Grafik: .144; Matrix: .178; t(38) = -0.5609; p = .578) noch in der Kontroll-Bedingung (Grafik-Kontrolle: .475; Matrix-Kontrolle: .617; t(16) = -1.375; p = .188). Es ist aber zu beachten, daß in beiden Fällen jeweils in der Matrix-Bedingung eine höhere Häufigkeit der Anwendung der optimalen Strategie feststellbar ist.
Wird eine Korrelation von mindestens .99 als Kriterium für die Identifikation des Einsatzes der Strategie verwendet, dann unterscheiden sich die verschiedenen Bildschirmpräsentationen sogar deutlicher: Bei den Experimental-Gruppen ist der Effekt der Bildschirmpräsentation auf die mittlere Häufigkeit der Anwendung der Strategie nicht signifikant (Grafik: .175; Matrix: .256; t(38) = 1.019; p = .315); bei den Kontroll-Gruppen erreicht dieser Effekt Signifikanz (Grafik-Kontrolle: .633; Matrix-Kontrolle: .822; t(16) = 2.158; p = .046).
Tabelle 7 zeigt die Anwendung der optimalen Strategie bei den Versuchspersonen, die dieses Prinzip mindestens drei Mal angewandt haben (Match > .75). Dabei fällt auf, daß auch nach erstmaliger Anwendung der Strategie immer wieder Aufgaben auftauchen, bei denen sie nicht angewandt wird.
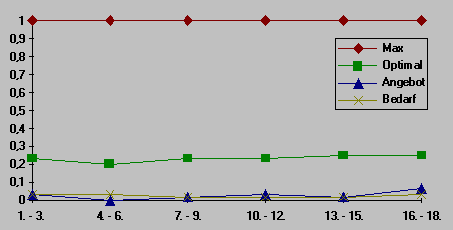
Der Verlauf der Anwendung der optimalen Strategie
Die Häufigkeit der Anwendung der optimalen, der Angebots- und der Bedarfsstrategie bei einem Match von mindestens .99, .75 und .6 wurden untersucht. Am interessantesten scheint dabei die Betrachtung bei einem Match von .75 zu sein, da bei diesem die einzelnen Strategien noch gut anhand der Daten unterschieden werden können (erkennbar unter anderem daran, daß in den Kontrollgruppen keine Anwendung der Angebots- oder der Bedarfsstrategie diagnostiziert wird).
Die Häufigkeit der Anwendung der optimalen Strategie, die für die experimentelle Grafik-Gruppe in Abbildung 7 zu sehen ist, (gemittelt über alle Versuchspersonen in der Grafik-Bedingung und jeweils sechs aufeinander folgende Aufgaben) bleibt in der Grafik-Bedingung relativ konstant (.217, .233 und .25 bei den ersten bis dritten sechs Aufgaben).
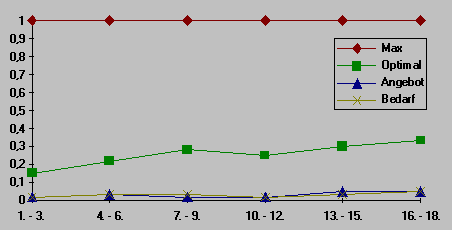
Abbildung 8:
Die Entwicklung der Häufigkeit der Anwendung der verschiedenen Strategien in der Matrix-Bedingung bei Match > .75. Max steht für den theoretisch maximal erreichbare Häufigkeit der Anwendung einer Strategie; Optimal bezieht sich auf die Anwendung der optimalen Strategie, Angebot auf die Anwendung der Angebotsstrategie und Bedarf auf die Anwendung der Bedarfsstrategie. Die Werte auf der Abszisse stehen für den Mittelwert von jeweils drei aufeinanderfolgenden Aufgaben.
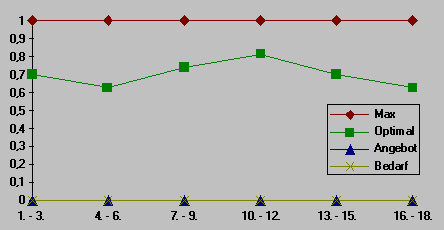
Abbildung 9:
Die Entwicklung der Häufigkeit der Anwendung der verschiedenen Strategien in der Grafik-Kontroll-Bedingung bei Match > .75. Max steht für den theoretisch maximal erreichbare Häufigkeit der Anwendung einer Strategie; Optimal bezieht sich auf die Anwendung der optimalen Strategie, Angebot auf die Anwendung der Angebotsstrategie und Bedarf auf die Anwendung der Bedarfsstrategie. Die Werte auf der Abszisse stehen für den Mittelwert von jeweils drei aufeinanderfolgenden Aufgaben.
In der Matrix-Bedingung dagegen, die in Abbildung 8 zu sehen ist, scheint eine leichte Zunahme der Häufigkeit der Anwendung der optimalen Strategie aufzutreten: bei den ersten sechs Durchgängen beträgt die Häufigkeit der Anwendung dieser Strategie .183, bei den mittleren sechs Durchgängen beträgt sie .267 und bei den letzten sechs Durchgängen wird sie mit einer Häufigkeit von .317 angewandt.
Zur Untersuchung der Anwendung der optimalen Strategie, die für die einzelnen Gruppen in den Abbildungen 7 - 10 zu sehen ist, wurde eine mehrfaktorielle Varianzanalyse mit den Faktoren Block (1. - 3. Aufgabe; 4. -6. Aufgabe usw.), Gruppe (Experimental- und Kontroll-Gruppe) und Bildschirmpräsentation berechnet. Die abhängige Variable nahm dabei den Wert 1 an, wenn die entsprechende Aufgabe nach der optimalen Strategie gelöst worden war (die Identifikation erfolgte durch einen Match mit der vorhergesagten Operatorfolge von mindestens .75), und den Wert 0 sonst. Dabei zeigt sich kein signifikanter Effekt des Faktors Block (F(5;270) = 1.629; p = .152); der Effekt des Faktors Bildschirmpräsentation (F(1; 54) = 0.369; p = .546) ist ebenfalls genauso wenig signifikant wie sämtliche Interaktionen zwischen den einzelnen Faktoren. Nur der Faktor Gruppe wirkt sich sehr signifikant (F(1;54) = 44.964; p < .0005) auf die Häufigkeit der Anwendung der optimalen Strategie aus.
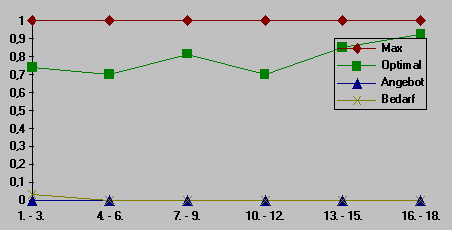
Die Zeit bis zur ersten Aktion
Die Zeit, die nach der vollständigen Präsentation der Aufgabe vergeht, bis die Versuchsperson die erste Verbindung anwählt, kann als Indikator für die zu Beginn der Aufgabe notwendige Planungstätigkeit betrachtet werden. Diese Zeiten sind für die verschiedenen Bedingungen in Abbildung 11 dargestellt.
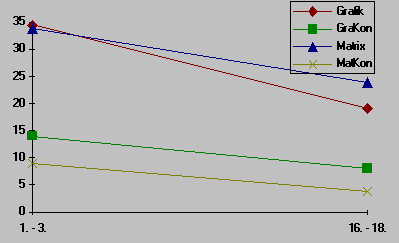
Abbildung 11: Die Latenz der ersten Aktion im Verlauf des Experiments.
Die Werte der y-Achse sind die durchschnittlichen Zeiten in Sekunden, die bis zur ersten Aktion der Versuchsperson vergangen sind. Der erste Wert ist der Mittelwert der 1. bis zur 3. Aufgabe, der zweite Wert ist der Mittelwert der 16. - 18. Aufgabe. Matrix und Grafik sind die beiden experimentellen Bedingungen, MatKon und GraKon stehen für die beiden Kontroll-Gruppen.
Der Faktor Aufgabenblock (die wievielte Aufgabe im Experiment bearbeitet werden soll) übt einen signifikanten Einfluß auf diese Planungszeit aus (F(1; 54) = 4.183; p < .0005). Ob es sich um die Experimental- oder um die Kontroll-Gruppe handelt, hat ebenfalls einen signifikanten Einfluß (F(1; 54) = 20.388; p < .0005). Der Faktor Bildschirmpräsentation wirkt sich nicht aus (F(1; 54) = 0.001; p = .977). Die Interaktionen zwischen den genannten Faktoren sind ebenfalls alle nicht signifikant (alle > .47).
Der relative Geschwindigkeitszuwachs ist bei der Experimental-Gruppe etwa genauso hoch (.60) wie bei der Kontroll-Gruppe (.59). Allerdings liegt die Planungszeit bei der Experimental-Gruppe auch nach 18 Übungsdurchgängen (21.6 Sekunden) noch deutlich über der Zeit, die in der Kontrollgruppe beim ersten Durchgang benötigt wurde (12.8 Sekunden).
In der Experimental-Gruppe unterscheiden sich die beiden Bildschirmpräsentationen nicht signifikant hinsichtlich der Häufigkeit der Anwendung der optimalen Strategie. Die Art der Präsentation der Aufgabenstellung scheint also den Gebrauch der optimalen Strategie nicht zu beeinflußen. In der Kontrollgruppe wird zwar die optimale Strategie unter der Grafik-Bedingung signifikant seltener angewandt als unter der Matrix-Bedingung; dies muß aber an den bei der Abarbeitung der Strategie auftretenden Fehlern liegen, da ja beide Gruppen gleichermaßen instruiert worden waren, die optimale Strategie zu befolgen.
Die erstaunlich niedrige Häufigkeit der Anwendung der optimalen Strategie in den Kontrollgruppen (Grafik .475, Matrix .617 bei Identifikation durch einen Match von 1 bezüglich der Strategie) zeigt, daß die Instruktion, diese Strategie genau zu befolgen, nicht immer eingehalten wurde. Dies kann unter anderem daran liegen, daß wegen der Vielzahl der dargestellten Informationen leicht Fehler bei der Anwendung der Strategie auftraten (wie z.B. das Übersehen eines niedrigen Kostenwertes).
Die optimale Strategie wird in den Experimental-Gruppen auch nach mehrmaliger Anwendung nicht konsequent beibehalten. Es findet also entweder keine Einsicht in die Optimalität der Strategie statt oder die Strategie wird nicht explizit angewandt, sondern die auch von der Strategie vorhergesagte Operatorfolge ergibt sich aus der Bearbeitung der Aufgabe mittels lokaler Strategien. Ein weiterer Grund kann darin liegen, daß auch bei beabsichtigter Anwendung der Strategie relativ häufig Fehler unterlaufen (vergleiche die Kontrollgruppen, bei denen ebenfalls nicht alle Aufgaben nach der optimalen Strategie gelöst werden, da Fehler bei ihrer Abarbeitung auftreten), die dann wegen des entsprechenden Feedbacks zu einem Strategiewechsel führen können.
Die Häufigkeit der Anwendung der optimalen Strategie verändert sich nicht signifikant im Laufe des Experimentes mit zunehmender Übung. Dies scheint daran zu liegen, daß auch nach erfolgreicher Anwendung der optimalen Strategie diese nicht beibehalten wird. Dafür kann es zwei Ursachen geben: Bei der beabsichtigten Anwendung der optimalen Strategie können Fehler auftreten und zu einer suboptimalen Lösung führen, was einen Strategiewechsel bei der Versuchsperson induzieren kann. Eine zweite Ursache kann darin bestehen, daß auch die Anwendung anderer Strategien häufig zu einer optimalen Lösung führt. Weil das Feedback, das auf eine optimale Lösung folgt, nicht nur nach Anwendung der optimalen Strategie gegeben wird, verliert es hinsichtlich der Verstärkung der Anwendung dieser Strategie an Wirkungskraft.
Die sehr niedrigen Anwendungshäufigkeiten der anderen teilweise verbalisierten Strategien (Angebots- oder Bedarfsstrategie) deuten darauf hin, daß die Aussagen der Versuchspersonen zu ihrer Lösungsstrategie nicht unbedingt ihrem tatsächlichen Vorgehen entsprechen. Mit zunehmender Übung ist also bezüglich der genauer untersuchten Strategien (optimale Strategie, Angebots- und Bedarfs-Strategie) keine deutliche Zunahme der Anwendungshäufigkeit, wie von Hypothese 7 vorhergesagt, nachweisbar.
Das in der experimentellen Bedingung auch nach dem Lösen von 21 Aufgaben lange Zeitintervall zwischen der vollständigen Präsentation der Aufgabe und der ersten Aktion der Versuchsperson, deutet auf eine immer noch nötige Planungstätigkeit hin; wäre es dagegen kurz (wie es bei den Kontrollgruppen der Fall ist), würde es nahe legen, daß nach einer bekannten Strategie vorgegangen wurde. Für die Versuchspersonen der Experimental-Gruppe scheinen (auch mit zunehmender Übung bei der Lösung der Aufgaben) zu Beginn der Aufgabe mehr Überlegungen notwendig zu sein als für die der Kontrollgruppe, die bereits wissen, was sie tun sollen. Dies widerlegt die Hypothese 7, nach der die Anwendung von Strategien zunehmen sollte und somit die nötige Planungszeit abnehmen müßte.
4.8. Die Verbalisierung von Strategien
Die Versuchspersonen wurden erst am Ende des Experimentes darum gebeten, sich zu den von ihnen verwendeten Strategien zu äußern. Während sie die Aufgaben bearbeiteten, wußten sie noch nicht, daß sie zu ihrer Vorgehensweise befragt werden würden. Dies kann dazu beigetragen haben, daß sie nicht explizit bestimmte Strategien testeten und verwendeten.
|
VP |
genannte Strategie |
n(o) |
n(A) |
n(B) |
VP |
genannte Strategie |
n(o) |
n(A) |
n(B) |
|
VP1g |
optimal |
15 |
1 |
1 |
VP1m |
andere |
2 |
0 |
0 |
|
Vp2g |
andere |
1 |
0 |
0 |
Vp2m |
andere |
0 |
0 |
0 |
|
VP3g |
Bedarf |
0 |
0 |
0 |
VP3m |
Bedarf |
0 |
0 |
0 |
|
VP4g |
Angebot |
0 |
0 |
1 |
VP4m |
Bedarf |
0 |
0 |
0 |
|
VP5g |
optimal |
6 |
0 |
0 |
VP5m |
optimal |
5 |
0 |
0 |
|
VP6g |
andere |
5 |
0 |
0 |
VP6m |
andere |
2 |
0 |
0 |
|
VP7g |
optimal |
6 |
0 |
0 |
VP7m |
optimal |
12 |
1 |
1 |
|
VP8g |
optimal |
12 |
0 |
0 |
VP8m |
andere |
2 |
1 |
0 |
|
VP9g |
optimal |
3 |
0 |
1 |
VP9m |
optimal |
13 |
0 |
0 |
|
VP10g |
optimal |
4 |
0 |
0 |
VP10m |
optimal |
6 |
0 |
1 |
|
VP11g |
andere |
2 |
0 |
1 |
VP11m |
optimal |
14 |
0 |
0 |
|
VP12g |
Bedarf |
0 |
1 |
3 |
VP12m |
optimal |
0 |
1 |
1 |
|
VP13g |
Bedarf |
0 |
1 |
1 |
VP13m |
optimal |
14 |
0 |
1 |
|
VP14g |
andere |
1 |
0 |
1 |
VP14m |
andere |
0 |
1 |
0 |
|
VP15g |
optimal |
13 |
0 |
0 |
VP15m |
optimal |
11 |
0 |
0 |
|
VP16g |
andere |
0 |
3 |
0 |
VP16m |
andere |
1 |
2 |
2 |
|
VP17g |
optimal |
7 |
0 |
0 |
VP17m |
Angebot |
1 |
0 |
1 |
|
VP18g |
optimal |
8 |
0 |
0 |
VP18m |
andere |
1 |
1 |
1 |
|
VP19g |
andere |
0 |
0 |
0 |
VP19m |
andere |
0 |
3 |
3 |
|
VP20g |
andere |
0 |
3 |
0 |
VP20m |
optimal |
8 |
0 |
1 |
Tabelle 8: Die Verbalisierung und die Anwendung von Strategien.
Für die einzelnen Versuchspersonen der experimentellen Grafik- (VP?g) und Matrix-Bedingung (VP?m) ist angegeben, welche Strategie in der postexperimentellen Befragung genannt wurde (optimal steht für die Nennung der optimalen Strategie, Angebot für die Angebots-Strategie und Bedarf für die Bedarfs-Strategie); andere bedeutet, daß keine der aufgeführten Strategien genannt wurde. Außerdem wird angegeben, bei wie vielen Aufgaben sich die Anwendung einer dieser Strategien durch einen Match von mindestens .75 identifizieren ließ; n(o) bezieht sich auf die optimale Strategie, n(A) auf die Angebots-Strategie und n(B) auf die Bedarfs-Strategie.
Berry und Broadbent (1984) konnten in einer Serie von Experimenten zeigen, daß bei der Kontrolle relativ komplexer Systeme zwar die Performanz mit zunehmender Übung steigt, die Fähigkeit, die angewandten Strategien zu verbalisieren (in einer postexperimentellen Befragung), dagegen nicht. Deshalb meinen sie, daß "assessing post-task knowledge solely by means of written questionnaire will not give a true picture of an individualīs competence" (Berry & Broadbent, 1984, S. 229; siehe aber z.B. Sanderson, 1989b). Deshalb sind die nach dem Experiment erhaltenen Verbalprotokolle mit Vorsicht zu interpretieren.
Aus den Verbalprotokollen ließen sich auch noch andere Strategien identifizieren, wie z.B. die Angebots- und die Bedarfsstrategie. Diese Strategien wurden aber nur sehr selten direkt angewandt: Die Angebotsstrategie ließ sich durch einen Match von 1.0 mit der vorhergesagten Operatorfolge mit einer Häufigkeit von .017 in der Grafik-Bedingung und .031 in der Matrix-Bedingung nachweisen; bei der Bedarfsstrategie waren es in der Grafik-Bedingung .022 und in der Matrix-Bedingung .017. Betrachtet man die in Tabelle 8 dargestellte Häufigkeit der Anwendung der jeweils von den Versuchspersonen genannten Strategien (identifiziert durch einen Match von mindestens .75 zwischen von der Strategie vorhergesagten und der tatsächlichen Operatorfolge), so fällt auf, daß insbesondere bei Nennung der Angebots- und Bedarfs-Strategie diese nur selten auch tatsächlich angewandt werden. Auch bei einigen Versuchspersonen, die in der postexperimentellen Befragung angaben, nach der optimalen Strategie vorgegangen zu sein, ließ sich nur eine geringe tatsächliche Häufigkeit der Anwendung dieser Strategie nachweisen.
Ericsson und Simon (1984, S.15) haben folgende Vorstellung von Verbalprotokollen: "Within our theoretical framework, we can represent verbal reports as bringing information into attention, then, when necessary, converting it into verbalizable code, and finally, vocalizing it."
Wird eine Versuchsperson befragt, so ist nur die im Arbeitsgedächtnis befindliche Information direkt zugänglich (cf. Ericsson & Simon, 1984). Muß Information dagegen erst aus dem Langzeitgedächtnis abgerufen werden, ist eine zusätzliche Stufe des Abrufes notwendig, die Fehler oder Unvollständigkeiten bewirken kann. Es ist auch schwierig, "to separate information that was heeded at the time of a specific episode from information acquired previously or subsequently that is associated with it" (Ericsson & Simon, 1984, S. 19). Deshalb wurden sofort nach der Lösung der letzten Aufgabe die Versuchspersonen gefragt, wie sie diese gelöst hätten.
Nur sehr wenige Versuchspersonen berichteten, daß sie bei der Lösung verschiedener Aufgaben unterschiedliche Strategien verwendet hätten, obwohl davon auszugehen ist, daß nicht alle Aufgaben auf die gleiche Weise gelöst worden waren (sonst hätten die Versuchspersonen die verwendete Strategie sofort und ohne weiteres Nachdenken/Nachfragen nennen können). Außerdem fiel auf, daß im Verlauf der Befragung die Versuchspersonen die verwendete Strategie immer deutlicher formulieren konnten, wie es von Hypothese 8 vorhergesagt wird.
Die geringe Häufigkeit der Anwendung der verbalisierten Strategien trotz ihrer Nennung läßt sich dadurch erklären, daß die Versuchspersonen zwar "im Prinzip" entsprechend diesen Strategien die ersten Schritte unternahmen, dann aber, nachdem die Freiheitsgrade durch die bereits erstellte Teillösung drastisch verringert waren, in Abhängigkeit von der konkreten Aufgabe und unter Verwendung lokaler Strategien (Teilstrategien) die restlichen Einheiten vergeben haben.
Es ist wahrscheinlich, daß erst die Befragung dazu führte, daß die verwendete Strategie der Versuchsperson explizit bewußt wurde. Möglicherweise entstand auch erst durch die Befragung bei den Versuchspersonen der Eindruck, daß die meisten Aufgaben nach der von ihr genannten Strategie gelöst worden waren. Gerade bei ungünstiger Fragestellung "the answers can be generated (inferred) without access to a specific memory trace of the episode" (Ericsson & Simon, 1984, S. 20).
Das von VanLehn (1991) beschriebene charakteristische Verhalten, das sich in Verbalprotokollen zum Zeitpunkt des Erwerbs von Regeln zeigen sollte, ließ sich in dem von mir durchgeführten Experiment nicht nachweisen, da hier die Versuchspersonen erst nach Beendigung aller Aufgaben befragt wurden.
5. Allgemeine Diskussion
Im folgenden soll nun versucht werden, die dargestellten empirischen Befunde in Hinblick auf die eingangs betrachteten Faktoren, die bei der Bearbeitung der Aufgaben eine Rolle spielen, zu interpretieren.
Es wurde versucht, die Präsentation der Information und die Eingabe der Lösung möglichst benutzerfreundlich zu gestalten, um den kognitiven Aufwand zur Bedienung der Oberfläche möglichst niedrig zu halten und die schnelle Erlernbarkeit der Bedienung zu ermöglichen. Die beiden Bildschirmpräsentationen wurden so gestaltet, daß die eingangs aufgeführten von Shneiderman (1987) für ergonomische Benutzeroberflächen geforderten Kriterien berücksichtigt wurden. Zu den einzelnen Kriterien läßt sich folgendes anmerken:
Die jeweiligen Informationen zu den Kosten, zum Angebot und zum Bedarf wurden immer an der gleichen Stelle am Bildschirm dargeboten. Die Beschriftung der einzelnen Orte blieb ebenfalls immer gleich. Somit sollten Konsistenz und Ortskonstanz gewährleistet sein.
Die effektive Informationsaufnahme sollte dadurch erleichtert werden, daß versucht wurde, die einzelnen Informationen sinnvoll zu gruppieren. Bei der Matrix-Bedingung mußte an einer Stelle absichtlich gegen dieses Prinzip verstoßen werden: Die Anzeige des verbleibenden Angebots/Bedarfs in der Matrix-Bedingung sollte sinnvollerweise neben der entsprechenden Zeile/Spalte der Matrix stehen. Wäre dies aber so verwirklicht worden, hätten sich andere Zeiten für die Encodierung der Aufgabe ergeben, da die Versuchsperson dann den Blick nicht mehr von den Kosten abwenden hätte müssen, um das Angebot bzw. den Bedarf zu ermitteln. Dadurch wäre ein zusätzlicher Unterschied in der Encodierung zwischen den beiden Bildschirmpräsentationen eingeführt worden.
Die Minimierung der Gedächtnisbelastung sollte dadurch erzielt werden, daß alle nötigen Informationen permanent am Bildschirm dargeboten wurden, so daß keine Informationen im Gedächtnis behalten werden mußten.
Die Kompatibilität der Bildschirmdarstellung mit der Dateneingabe wurde in der Grafik-Bedingung dadurch sichergestellt, daß direkt in der Bildschirmdarstellung der vergebenen Einheiten deren Wert verändert werden konnte; es sollte also eine direktmanipulative Eingabe möglich sein. In der Matrix-Bedingung erfolgte die Selektion der Verbindung direkt in der Anzeige der Werte und auf dem Eingabefeld war nochmals schriftlich die Verbindung vermerkt, auf die sich die Eingabe auswirkte.
Auf die flexible Kontrolle des Benutzers über die Datendarstellung mußte verzichtet werden, da die Bildschirmgestaltung möglichst konstant bleiben mußte, um Aussagen über ihre Auswirkungen treffen zu können.
Allgemein wurde zwar versucht, die einzelnen Informationen möglichst übersichtlich am Bildschirm zu präsentieren, aber wegen der Vielzahl der zur Lösung der Aufgaben nötigen Informationen war dies nur bedingt möglich.
Bei beiden Bildschirmpräsentationen handelt es sich um graphische Benutzeroberflächen mit Direktmanipulation entsprechend den Anforderungen von Shneiderman (1987): Außer bei der Präsentation einer neuen Aufgabe waren die Antwortzeiten des Systems so kurz, daß der Eindruck entstand, die Reaktion wäre sofort erfolgt. Die Direktmanipulation bestand in der graphischen Bedingung darin, daß die zu vergebenden Einheiten mit einem Schieberegler direkt "verschoben" werden konnten; dadurch sollte der Eindruck entstehen, daß die gewünschte Aktion direkt ausgeführt wird und nicht, daß man nur mit einer Schnittstelle zum Computer kommuniziert. In der Matrix-Bedingung kann die gewünschte Verbindung immerhin noch direkt durch Darauf-Zeigen angewählt werden und der gewünschte Zahlenwert eingegeben werden.
Durch die auf diese Weise realisierte Direktmanipulation sollten die Versuchspersonen das Gefühl haben, direkt die Einheiten zu vergeben und auf diese Weise sollte die Kluft zwischen den psychologischen Variablen der Versuchspersonen (ihren Zielen und Absichten) und den physikalischen Variablen des Systems (der Anzahl an Einheiten auf einer Verbindung) verringert werden (siehe Norman, 1986).
Svendsen (1991) berichtet, daß eine effiziente und leicht anwendbare Benutzeroberfläche dazu führte, daß sich kaum Strategieerwerb nachweisen ließ, da die Versuchspersonen einfach einzelne Schritte ausprobierten und deren Resultat am Bildschirm betrachteten, so daß die mentale Ausführung der Lösungsschritte nicht nötig war und deshalb auch keine Bearbeitungsstrategie gelernt wurde. In dem hier beschriebenen Experiment kann dieser Fall ebenfalls aufgetreten sein: Das Ausprobieren einzelner Lösungsschritte war für die Versuchspersonen nur mit relativ geringen Kosten verbunden, da ein Schritt relativ leicht wieder rückgängig zu machen war; es bot aber andererseits den Vorteil, daß die sich ergebende Situation nicht ausgerechnet werden mußte. Dies zeigte sich insbesondere darin, daß in der Grafik-Bedingung, bei der die Eingabe etwas leichter und schneller erfolgt als in der Matrix-Bedingung, mehr überflüssige Schritte gemacht werden; die ergonomischere Benutzeroberfläche führt also zu einem weniger überlegtem Eingeben von Schritten.
Bei der Eingabe der Lösungen wurde auch eine gewisse Fehlertoleranz, die von ergonomischen Schnittstellen zwischen Mensch und Maschine immer wieder gefordert wird, verwirklicht: Zu hohe eingegebene Werte, die nicht realisierbar waren, wurden automatisch auf den maximal möglichen Wert herabgesetzt. Auf diese Weise konnten keine ungültigen, sondern nur unvollständige Lösungen entstehen.
Den Versuchspersonen wurden nach Beendigung des Experiments und der anschließenden Befragung je ein Ausdruck des Bildschirms der beiden Präsentations-Bedingungen (wie sie in Anhang A und Anhang B abgebildet sind) gezeigt. Dabei empfanden alle Versuchspersonen diejenige Art der Bildschirmpräsentation als "leichter", die auch bei ihnen im Experiment verwendet wurde. Der wiederholte Umgang mit einem bestimmten Bildschirm-Design und die daraus resultierende Übung im Umgang mit diesem führte also dazu, daß diese auch Alternativen gegenüber vorgezogen wird.
5.2. Der Einfluß des Zahlenmaterials
Ob die Versuchspersonen bei der Lösungssuche das Ergebnis der Operatoranwendungen (zumindestens teilweise) mental evaluierten, also die Kosten der resultierenden Situation berechneten, läßt sich nur anhand der Auswirkungen der verschiedenen isomorphen Aufgabenvarianten beurteilen. Dazu ist vorneweg nochmals daran zu erinnern, daß der Effekt dieser Variationen nicht signifikant war, in der Experimental-Gruppe jedoch beinahe das vereinbarte Signifikanzniveau erreichte (p = .064). In der Kontroll-Gruppe war der selbe Effekt dagegen deutlich nicht signifikant (p = .709).
Wird zur Lösung der Aufgaben eine Strategie angewandt, bei der die Verbindungen, auf denen die Einheiten vergeben werden sollen, nur nach ihren relativen Kosten gewählt werden, sollte sich ein gewisser Unterschied in den Lösungszeiten zwischen den Varianten groß-eng (Mittelwert bei den Experimental-Gruppen: 122.6 Sekunden) und groß-weit (Mittelwert bei den Experimental-Gruppen: 121.5 Sekunden) zeigen, da ordinale Informationen bei weiter auseinanderliegenden Zahlen schneller und sicherer gefunden werden. Dieser Unterschied zeigte sich aber nicht. Er ließ sich auch in der Kontroll-Gruppe, die eigentlich instruiert worden war, nur die relative Position der Kosten zu beachten, nicht nachweisen: Dort lagen die durchschnittlichen Bearbeitungszeiten für die Variation groß-weit (70.1 Sekunden Mittelwert) sogar etwas über den entsprechenden Werten der Variation groß-eng (69.5 Sekunden Mittelwert). Wegen des unterschiedlichen Aufwandes für die Rangreihenbildung sind allerdings keine sonderlich großen Unterschiede in den Lösungszeiten zu erwarten: Die Daten von Dehaene (1989) zeigen, daß die Unterschiede in der für den Zahlenvergleich benötigten Zeit nicht mehr als 100 Millisekunden betragen, wenn die Distanz zwischen den Zahlen zwischen 1 und 20 variiert.
Bei Anwendung der Strategie in den Kontroll-Gruppen muß zur Erstellung eines Schrittes der jeweils nächsthöhere Kostenwert gefunden werden. Der Abstand zwischen den Kosten wirkte sich jedoch nicht auf die Bearbeitungszeit der jeweiligen Aufgabe aus; dies läßt sich folgendermaßen erklären: Bei der Variation mit den eng beieinander liegenden Kostenwerten betrug der Abstand zwischen den einzelnen Zahlen nur 1. Deshalb haben die Versuchspersonen in diesem Fall möglicherweise den nächsthöheren Kostenwert selbst "erzeugt" (durch Addition von 1 auf den gerade betrachteten Wert) und dann diesen Wert nur noch am Bildschirm gesucht; auf diese Weise werden Größenvergleiche überflüssig. Bei den Kostenwerten mit den größeren Abständen dagegen wurde wohl von einem Wert ausgehend tatsächlich versucht, den nächsthöheren zu finden; dies sollte aber aufgrund des höheren Abstandes zwischen den Zahlen relativ leicht fallen. Offenbar war der Zeitaufwand in beiden Fällen etwa gleich hoch.
Außerdem unterstützte möglicherweise die zusätzliche Visualisierung der Kostenhöhe in der Höhe des Schiebereglers (Grafik-Bedingung) bzw. in der Breite des Rechteckes über der numerischen Darstellung der Kosten (Matrix-Bedingung) die Vergleichsprozesse.
Wenn die Versuchspersonen bei der Lösungssuche tatsächlich rechnen, sollten die Lösungszeiten unter anderem von der Höhe der Kosten abhängen, weil die für mentale Arithmetik benötigten Zeiten mit der Höhe der auftretenden Zahlenwerte zunehmen (siehe oben). Dies war auch der Fall (auch wenn die Unterschiede knapp nicht signifikant waren): Die Zeiten in der Experimental-Gruppe lagen bei der Variation klein-eng (111.8 Sekunden Mittelwert) deutlich unter denen der Variationen groß-eng (122.6 Sekunden Mittelwert) und groß-weit (121.5 Sekunden Mittelwert). Die letzten beiden Variationen unterschieden sich kaum; da jedoch bei diesen beiden Variationen große Zahlen vorkommen, sollte auch in dem Rechenaufwand kein all zu großer Unterschied auftreten.
In den Kontrollgruppen lagen die durchschnittlichen Lösungszeiten für die Variation klein-eng nur sehr wenig (67.4 Sekunden Mittelwert) unter den übrigen Lösungszeiten (groß-eng: 69.5 Sekunden; groß-weit: 70.1 Sekunden); der Effekt des Faktors isomorphe Aufgabenvariation war deutlich nicht signifikant..
Der deutliche Unterschied bei den Experimental-Gruppen läßt sich damit erklären, daß wahrscheinlich zumindest ein Teil der Versuchspersonen bei der Lösungssuche Berechnungen durchführte. In den Kontroll-Gruppen trat dagegen kaum ein Unterschied in den Lösungszeiten zwischen den Aufgabenvarianten auf, da dort für die Befolgung der Strategie keine Berechnungen nötig waren.
5.3. Work-Load und Strategie-Erwerb
In der experimentellen Matrix-Bedingung herrscht aus den oben beschriebenen Gründen eine höhere Belastung des Arbeitsgedächtnisses als in der Grafik-Bedingung; diese wirkt sich in längeren Lösungszeiten und einem etwas verlangsamten Lernverlauf aus. Bei den Kontroll-Gruppen treten diese Unterschiede zwischen den Bildschirmpräsentationen nicht auf, da dort nur eine bekannte Strategie abgearbeitet werden muß und somit keine hohe Belastung des Arbeitsgedächtnisses - z.B. durch Speicherung von mental evaluierten Zwischenergebnissen - auftritt.
Die höhere Belastung des Arbeitsgedächtnisses in der Matrix-Bedingung kann auch dazu führen, daß darin enthaltene Elemente öfters verloren gehen (siehe Anderson, 1987) und deshalb aus der Bildschirmrepräsentation erneut abgelesen werden müssen. Dafür ist ein zusätzlicher Zeitaufwand erforderlich. So läßt sich ein Teil der längeren Lösungszeiten bei der Matrix-Präsentation erklären.
Im Verlauf des Experiments fand bei den Experimental-Gruppen kaum Strategieerwerb statt. Dies läßt sich an mehreren Aspekten in den Daten zeigen:
Keine Verbesserung der Lösungsgüte
Ein wichtiges Indiz dafür, daß im Verlauf des Experiments kein oder nur wenig Strategieerwerb stattfand, besteht darin, daß die Lösungen mit zunehmender Erfahrung im Umgang mit den Aufgaben nicht besser wurden: die durchschnittliche Distanz zum Optimum änderte sich nicht signifikant im Verlauf des Experiments.
Keine Verbesserung der Effizienz der Lösung
Die Anzahl der überflüssigen Schritte liegt in den Kontroll-Gruppen, also bei Anwendung einer Strategie, signifikant niedriger als in den Experimental-Gruppen. Das Abarbeiten einer Strategie sollte also eine verringerte Anzahl an überflüssigen Schritten zur Folge haben. Im Verlauf des Experimentes ließ sich jedoch für die Experimental-Gruppen keine signifikante Änderung der Häufigkeit der überflüssigen Schritte nachweisen; es scheinen also nicht vermehrt Strategien angewandt zu werden.
Gleiche Steigerung der Lösungsgeschwindigkeit
Der etwa gleiche Lernfortschritt bezüglich der Lösungszeiten für die Experimental- und die Kontroll-Gruppen - zu sehen in den nicht signifikanten Unterschieden in den Steigungsparametern der nach dem power-law gefitteten Lernkurven - läßt sich folgendermaßen erklären: Der Lernfortschritt in der Kontroll-Gruppe kann nur auf einer Steigerung der Effizienz der Encodierung der Aufgabenstellung und der mechanischen Fertigkeiten beim Eingeben der Lösungen beruhen, da die Strategie zur Bearbeitung der Aufgaben bereits von Anfang an bekannt war. Bei den Experimental-Gruppen, bei denen die Gesamt-Lösungszeit deutlich höher liegt als bei den Kontroll-Gruppen, gehen wegen der höheren Work-Load auch öfter Elemente der Aufgabenstellung aus dem Arbeitsgedächtnis verloren (siehe Anderson, 1987). Deshalb müssen deutlich öfter als bei den Kontroll-Gruppen relevante Informationen encodiert werden.
Geht man davon aus, daß kein Strategieerwerb stattfindet, sollte sich bei den Experimental-Gruppen die nötige Anzahl der Encodierungen nicht verringern. In den Kontroll-Gruppen sollte sie ebenfalls gleich bleiben, weil dort von Anfang an die selbe Strategie angewandt wird. Da sich bei beiden Bedingungen die Häufigkeit der Encodierung von Informationen also kaum ändert und eine Abnahme der Lösungszeiten vor allem auf einer Beschleunigung der Encodierung beruht, ergibt sich somit ein etwa gleich schneller Lerngewinn.
Würde in der Experimental-Bedingung dagegen Strategieerwerb stattfinden, müßte der Lernfortschritt dort deutlicher ausfallen, weil außer durch die effizientere Encodierung der Aufgaben auch durch effizientere Bearbeitungsstrategien eine Verringerung der Bearbeitungszeit der Aufgaben auftreten sollte. Dies ist jedoch (siehe oben) nicht der Fall.
Keine Abnahme der "Planungszeit"
Die Zeit, die zwischen der Präsentation der Aufgabenstellung und der ersten Aktion der Versuchsperson verstreicht, kann nach Carlson, Khoo, Yaure und Schneider (1990) als Indiz für Planungstätigkeit gesehen werden: Sie interpretieren eine Abnahme der Latenz der ersten Aktion der Versuchsperson dahingehend "that solution plans became more accessible with practice" (Carlson, Khoo, Yaure & Schneider, 1990, S. 210). Die Dauer dieses Zeitintervalls liegt in der Experimental-Gruppe auch am Ende des Experiments noch über dem entsprechenden Wert, der die Kontroll-Gruppen zu Beginn des Experimentes kennzeichnet. Wenn die Versuchspersonen eine bestimmte Strategie (egal welche) verfolgen würden, dann müßten sie auch sofort mit der Abarbeitung der selbigen beginnen können und der Zeitraum zwischen der Präsentation der Aufgabenstellung und der ersten Aktion der Versuchsperson sollte nicht wesentlich länger als bei den Kontroll-Gruppen dauern. Auch dies scheint nicht der Fall gewesen zu sein.
Auch wenn die Belastung des Arbeitsgedächtnisses bei den Experimental-Gruppen, wie gezeigt, in der Grafik-Bedingung etwas niedriger liegt als in der Matrix-Bedingung, ist sie dennoch bei beiden Formen der Bildschirmpräsentation sehr hoch, da die Aufgaben aus sehr vielen interagierenden Elementen bestehen. Bei den Kontroll-Gruppen liegt die Work-Load dagegen deutlich niedriger, da zur Abarbeitung der bekannten Strategie jeweils nur wenige Elemente im Arbeitsgedächtnis gehalten werden müssen.
Der Erwerb von Gesamt-Strategien:
Die Kapazität des Arbeitsgedächtnisses ist bei den Experimental-Gruppen bereits durch die Repräsentation der Aufgabe und die Speicherung von Zwischenergebnissen bei der Lösungssuche so weit ausgelastet, daß kein Strategieerwerb (bezüglich einer Gesamt-Strategie) stattfindet, da die gesamte Kapazität des Arbeitsgedächtnisses für die Lösung der Aufgaben aufgewandt werden muß (vergleiche Sweller, 1988; Sweller, Chandler, Tierney & Cooper, 1990; Hussy, 1991).
Zum Erlernen von Gesamt-Strategien müßte die Vorgehensweise beim gesamten Lösen der Aufgaben im Gedächtnis behalten werden. Da aber das Gedächtnis durch die Abarbeitung der Aufgaben so stark beansprucht wird, ist dies nicht möglich. Somit bleibt auch der Erwerb einer Gesamt-Strategie aus. In beiden Bedingungen wird jede Lösung praktisch neu erzeugt, falls nicht die optimale Strategie als solche erkannt wurde (was nur bei relativ wenigen Versuchspersonen der Fall zu sein schien). Das in beiden Fällen gleiche "ungeregelte" Vorgehen bei der Lösungssuche führt schließlich auch dazu, daß sich die Häufigkeit der optimalen Lösungen und die durchschnittliche Distanz zum Optimum nicht zwischen den beiden Bedingungen unterscheiden.
Der Erwerb von lokalen Strategien:
Es ist jedoch durchaus möglich, daß die Versuchspersonen Teil-Strategien (lokale Strategien), die sich auf die Bearbeitung von Teilzielen (wie zum Beispiel das Festlegen der Anzahl der zu transportierenden Einheiten) beziehen, die während der Bearbeitung der Aufgaben auftreten können, bilden und auch anwenden. Diesen Gedankengang greifen z.B. auch Carlson, Khoo, Yaure und Schneider (1990) mit ihrer Unterscheidung von search strategies und dem subgoal level auf: "With practice in a problem domain, certain sequences of operators will be repeated in order to achieve subgoals specified by high-level search strategies. This repetition allows for the development of an intermediate level of organization, which we refer to as the subgoal level" (Carlson et al., 1990, S. 194; Hervorhebung im Text).
In dem Experiment fand ein Erwerb lokaler Strategien statt, die sich nur auf einen einzelnen Schritt beziehen und zu deren Erlernen nicht mehrere Schritte im Gedächtnis gehalten werden müssen (so daß trotz der hohen Belastung des Arbeitsgedächtnisses ein Erlernen möglich ist): Meist wird die Bearbeitung der Aufgabe bei dem billigsten Kostenfeld begonnen und fast immer werden auf den Verbindungen maximal viele Einheiten vergeben. Diese lokalen Heuristiken vereinfachen die Lösung der Aufgaben entscheidend, indem sie die Anzahl möglicher Aktionen drastisch reduzieren.
Alternative Erklärungen für das Ausbleiben des Strategie-Erwerbs
Wontorra und Krems (1989) nannten folgende weitere mögliche Erklärung für die Abwesenheit eines nachweisbaren Strategieerwerbes: Die Versuchspersonen, die in ihrem Experiment 10 mal das Spiel Othello zu bewältigen hatten, konnten wegen mangelnder Übung kein strategisches Wissen erwerben.
Nach Funke (1991) besteht die Lösung komplexer Probleme, zu denen die vorliegenden Aufgaben zugeordnet werden können, aus dem Erwerb und der Anwendung von Wissen. Bei den von ihm durchgeführten Experimenten konnten die Versuchspersonen zuerst in einer Wissenserwerbungs-Phase mit dem System vertraut werden, indem sie es erkundeten. In einer anschließenden Wissensanwendungs-Phase sollten die Versuchspersonen dann bestimmte Ziele erreichen. Diese Trennung der beiden Phasen wurde in dem hier beschriebenen Experiment nicht vollzogen: Die Versuchspersonen sollten von Anfang an möglichst gute Lösungen liefern. Durch diese Instruktion wurde möglicherweise der eher explorative Umgang mit den Aufgaben verhindert, so daß aus diesem Grund weniger Strategie-Erwerb stattfand.
Eine weitere Erklärung für das Ausbleiben des Strategie-Erwerbs kann darin gesehen werden, daß die Versuchspersonen ihre Lösungen nicht immer für optimal hielten (Häufigkeit in der experimentellen Matrix-Bedingung .372, in der entsprechenden Grafik-Bedingung .525). Dies könnte dazu geführt haben, daß die jeweils möglicherweise getestete Strategie nicht weiter angewandt wurde, da die Versuchsperson nicht an die Optimalität der durch sie erzeugten Lösungen glaubte.
Außerdem könnte, wie bereits beschrieben, der von Svendsen (1991) beschriebene Fall eingetreten sein, daß eine einfach bedienbare Benutzeroberfläche dazu führt, daß die Lösungsschritte ohne vorherige Evaluation ausprobiert werden.
Eine weitere mögliche Begründung dafür, daß kein Strategieerwerb stattfand, kann in der Präsentation des Feedbacks nach der Bearbeitung der Aufgaben gesehen werden: Bei einer suboptimalen Lösung wird zur Darstellung der Rückmeldung (wie hoch die Kosten der Lösung sind) der gesamte Bildschirm verdeckt, insbesondere die Aufgabenstellung und die Lösung der Versuchsperson. Da es sich bei diesen Informationen um mehr Elemente handelt als im Gedächtnis behalten werden könnten, ist die Lösung und die Aufgabenstellung nicht mehr für die Versuchsperson verfügbar. Sie kann somit nicht mehr nachträglich durch Betrachten der Lösung erkennen, wo sie ungünstig gehandelt hat. Außerdem treten auch bei der bewußten Anwendung der optimalen Strategie häufig Fehler vom Typ der Slips auf, wie sich bei den Ergebnissen der Kontroll-Gruppen zeigte. Deshalb kam es wahrscheinlich auch bei der beabsichtigten Anwendung der optimalen Strategie in den Experimental-Gruppen zu Fehlern und daraus resultierendem negativen Feedback; darum wurde die optimale Strategie daraufhin möglicherweise von den Versuchspersonen nicht weiter angewandt.
Die höhere Belastung des Arbeitsgedächtnisses bei der Matrix-Bedingung sollte eigentlich mit einer höheren subjektiven Beurteilung der Aufgabenschwierigkeit einhergehen (siehe Meshkati & Loewenthal, 1988). Dieser Effekt ließ sich aber in dem geschilderten Experiment nicht überprüfen: Die Versuchspersonen sollten die erste Aufgabe als "mittel"-schwierig einstufen und dann bei allen folgenden Aufgaben angeben, wie schwierig diese im Vergleich zu der ersten Aufgabe zu lösen gewesen wären. Die Beurteilung der Aufgabenschwierigkeit hängt bei den restlichen Aufgaben somit weder von der Art ihrer Präsentation am Bildschirm (die ja für jede Versuchsperson konstant bleibt) noch von der daraus resultierenden Belastung des Arbeitsgedächtnisses ab, sondern nur von dem Unterschied der Lösungsschwierigkeit gegenüber der ersten Aufgabe.
Unterschiede in der Beurteilung der Aufgabenschwierigkeit, die auf der durch die verschiedenen Präsentationen der Aufgabenstellung am Bildschirm hervorgerufenen Work-Load beruhen, lassen sich somit in den hier erhobenen Daten nicht nachweisen.
Die optimale Strategie ist sehr einfach und effizient. Man könnte deshalb vermuten, daß sie, wenn sie einmal angewandt wurde, als günstige Lösungsmöglichkeit erkannt wird und von da an beibehalten wird; hier wäre dann das Konzept der Einsicht zutreffend. Mehrere Argumente dagegen, daß Einsicht in die Optimalität der optimalen Strategie erfolgte, wurden bereits bei der Diskussion der Befunde zur Anwendung von Strategien genannt: Die Strategie wurde möglicherweise nicht explizit angewandt, auch andere Strategien konnten zu einer optimalen Lösung führen und bei der Anwendung der Strategie traten Fehler auf, die zu negativem Feedback führten. Es fand also kein "einsichtiges" Lernen statt.
5.4. Die Problemrepräsentation
In dem Experiment lag der Repräsentation, die sich die Versuchspersonen von der Aufgabenstellung bildeten, möglicherweise ein mentales Modell entsprechend der anfangs beschriebenen Definition zugrunde, das auf dem allgemeinen (und eben nicht immer günstigsten) Prinzip basierte, auf billigen Verbindungen möglichst viel zu vergeben und auf teueren Verbindungen wenig. Ein Indiz dafür besteht zum Beispiel darin, daß die meisten Versuchspersonen, die nicht die optimale Strategie erkannten (wie sich in der postexperimentellen Befragung zeigte), auf relativ teueren Verbindungen nur wenige Einheiten vergeben wollten, auch wenn sie dadurch eine suboptimale Lösung erzielten, weil auf noch teureren Verbindungen Einheiten vergeben werden mußten. Nach Sanderson (1989b) können derartige biases als Indiz für ein zugrundeliegendes mentales Modell betrachtet werden. Diese Überlegung gilt für beide Bildschirmpräsentationen gleichermaßen.
Die Aufgabenstellung des beschriebenen Experiments besteht aus relativ vielen Informationseinheiten: Es existieren je 9 Kostenfelder und "Vergabefelder" (die die Anzahl auf einer Verbindung zu vergebender Einheiten darstellen) und je 3 Angebots- und Bedarfs-Werte; außerdem sind noch jeweils drei Werte für das maximal verfügbare Angebot bzw. den maximal benötigten Bedarf vorhanden. Insgesamt werden also 30 numerische Werte auf dem Bildschirm angezeigt. Zwischen diesen Werten bestehen auch noch teilweise wechselseitige Abhängigkeiten (zwischen Vergabefeldern und restlichem Angebot bzw. Bedarf). Hier liegt ein Beispiel für den in der Literatur (z.B. Norman, 1986) dokumentierten trade-off zwischen Reichhaltigkeit der dargestellten Information und der Unübersichtlichkeit von deren Darstellung vor.
Die Komplexität einer Aufgabe hängt von der Anzahl der darin enthaltenen Elemente und den Beziehungen zwischen diesen ab (cf. Leplat, 1988). Im hier beschriebenen Experiment lag nach diesem Kriterium eine sehr hohe Komplexität der Aufgaben vor. Die Vielzahl an Information war mit Sicherheit zu umfangreich, um komplett im Arbeitsgedächtnis gehalten werden zu können. Ich gehe deshalb davon aus, daß jeweils vor allem die Teile der Information im Arbeitsgedächtnis präsent waren, die sich auf die Verbindung bezogen, die gerade geprüft wurde (Angebotsort, Zielort, Kosten, maximales Angebot und maximaler Bedarf) und daß die restliche Information bei Bedarf direkt vom Bildschirm abgelesen wurde. Es handelt sich also um external memory bzw. display-based reasoning. Das Konzept des display-based reasoning kann auch zur Erklärung dafür herangezogen werden, daß die Bearbeitungszeiten für die einzelnen Aufgaben mit zunehmender Übung abnehmen, auch wenn die Eingabezeiten nicht mit einbezogen werden: Der Zeitgewinn resultiert daraus, daß die Versuchspersonen eben jenes display-based reasoning erlernen, insbesondere das Encodieren der benötigten Informationen. Larkin (1989, S. 333, Hervorhebung im Original) schreibt dazu: "Display-based problem solving requires learning. Domain specific productions are required to get useful information from the display and to generate knowledge of where an object īwantsī to go."
Wird von der Versuchsperson eine Aktion ausgeführt, so werden anschließend auch die entsprechenden Werte für das restliche Angebot bzw. für den verbleibenden Bedarf am Bildschirm auf den neuesten Stand gebracht. Diese Werte müssen also nicht extra ausgerechnet werden; die Versuchsperson kann hierfür die Bildschirmanzeige verwenden. Wird allerdings vor Ausführung eines Schrittes dessen Resultat nicht mental evaluiert (verläßt sich also die Versuchsperson zu sehr auf das Display), kann es zu ungünstigen Situationen kommen, die es erforderlich machen, einen bereits ausgeführten Schritt wieder rückgängig zu machen. Dies müßte sich in einem überflüssigen Schritt zeigen. Allerdings zeigte sich empirisch nur eine geringe Häufigkeit solcher überflüssiger Schritte (durchschnittlich < 1 bei einer Aufgabe). Die Lösungsschritte werden also meist nicht "blind" ausprobiert, sondern vorher überdacht. Es gilt aber zu beachten, daß in der graphischen Bedingung die Häufigkeit der überflüssigen Schritte signifikant höher liegt als in der Matrix-Bedingung. Die einfachere Betätigung der Eingabe scheint also das Ausprobieren etwas zu begünstigen.
Die im Anschluß an das Experiment durchgeführte Befragung der Versuchspersonen erbrachte, daß die meisten Teilnehmer des Experiments vor allem Konzepte wie "Kosten", "Angebot" und "Bedarf" verwendeten. Dies kann durch die Art der Erklärungen und Instruktionen zu Beginn des Experimentes begründet sein. Es ist aber bemerkenswert, daß nur sehr wenige Versuchspersonen davon sprachen, bei der Lösung der Aufgaben tatsächlich an "Waggons" gedacht zu haben. Eine gewisse Abstraktionsleistung scheint deshalb in der Regel zu erfolgen.
Bei dem hier beschriebenen Experiment wurden isomorphe Varianten der Aufgaben - durch verschiedene Bildschirmpräsentationen realisiert - verwendet. Es zeigten sich eine Reihe von Unterschieden aufgrund der Präsentationsform.
Zusammenfassung der Befunde
Zusammenfassend ließen sich in den Experimental-Gruppen folgende Unterschiede aufgrund der Bildschirmpräsentation feststellen:
In bezug auf die Lösungsgüte oder die subjektiven Daten zu den Aufgaben unterschieden sich die Bildschirmpräsentationen dagegen nicht; auch die Verteilung der Lösungszeiten innerhalb der Aufgaben, die Häufigkeit des Beginnens einer Lösung mit der billigsten Verbindung und die Zeiten bis zum Tätigen der ersten Aktion unterschieden sich nicht zwischen den beiden Bildschirmpräsentationen.
Erklärung der Befunde
Diese aufgeführten Befunde lassen sich folgendermaßen erklären: Die Versuchspersonen der Experimental-Gruppen bildeten sich eine mentale Repräsentation der Aufgabe, die die zur Lösungsfindung benötigten Informationen nur teilweise beinhaltete; die restlichen Informationen wurden bei Bedarf direkt von der Präsentation der Aufgabe am Bildschirm abgelesen; durch den unterschiedlichen Aufwand für die Encodierung dieser Werte kamen die oben genannten Unterschiede zustande.
Grundlage der Lösungssuche bilden also die mentale Repräsentation und die Repräsentation der Aufgabe am Bildschirm. Von der Repräsentation der Aufgabe ausgehend versuchten die Versuchspersonen herauszufinden, welcher Schritt, d.h. die Vergabe von wie vielen Einheiten auf welcher Verbindung, zu dem kostengünstigsten Resultat führt; dazu wurde mental evaluiert, wie sich die Wahl eines Schrittes auswirken würde, d.h. welche neuen Kosten dadurch entstehen würden. Es wurde somit höchstens einen Schritt weit geplant. Die oben genannten Gemeinsamkeiten bei beiden Bildschirmpräsentationen sind darauf zurückzuführen, daß die Aufgaben so komplex sind, daß bei keiner der beiden Repräsentationen eine effiziente Suche nach einem Lösungsweg stattfinden kann. Es kann jeweils nur von der gerade vorliegenden Teillösung aus versucht werden, den nächsten Schritt zu optimieren.
Unterschiede in der mentalen Repräsentation
Die Unterschiede in der mentalen Repräsentation der Aufgaben entstehen aus den Unterschieden in der Präsentation der Aufgaben am Bildschirm:
Wenn die Versuchsperson nach der nächsten zu "bedienenden" Verbindung sucht, braucht sie - wenn nichts ausgebessert werden soll - nur jene Verbindungen betrachten, auf denen noch nichts vergeben wurde; bereits bearbeitete Felder brauchen im Normalfall nicht nochmals betrachtet werden. In der Grafik-Bedingung fallen die schon abgearbeiteten Verbindungen wegen des herausstehenden (sich nicht mehr in der Ausgangsstellung befindenden) Schiebereglers deutlicher auf als in der Matrix-Bedingung, wo dazu erst die entsprechenden numerischen Werte encodiert werden müssen. Deshalb ist es möglich, daß in der Grafik-Bedingung der Repräsentation der einzelnen Verbindungen ein Attribut schon abgearbeitet? zugeordnet ist, während dieses in der Matrix-Bedingung erst inferiert werden muß.
Ähnliches gilt für die Orte, an denen kein Angebot oder Bedarf mehr vorliegen. Diese fallen in der Grafik-Bedingung deutlicher auf, da dort dann der dunkle Balken, der noch verfügbares Angebot bzw. noch benötigten Bedarf codiert, verschwindet. In der Matrix-Bedingung müssen dagegen wiederum erst die entsprechenden numerischen Werte encodiert und als von Null verschieden klassifiziert werden. Das Attribut eines Ortes muß noch betrachtet werden? kann also in der Grafik-Bedingung direkt aus der Bildschirm-Darstellung des Ortes abgelesen werden (und ist somit Teil der mentalen Repräsentation dessen), während es in der Matrix-Bedingung erst erarbeitet werden muß.
Ein weiterer Unterschied zwischen der Grafik- und der Matrix-Bedingung kann darin bestehen, daß in der Matrix-Bedingung die Werte für das verfügbare Angebot bzw. den noch bestehenden Bedarf - zumindest zu Beginn - numerisch und "digital" repräsentiert werden müssen (da sie nur so am Bildschirm dargestellt werden). In der Grafik-Bedingung dagegen können diese Werte auch leicht "analog" mental repräsentiert werden, da die Werte am Bildschirm durch einen Balken zusätzlich visualisiert werden und somit die Orte mit dem meisten Angebot bzw. Bedarf sofort auffallen. Bei der Anwendung der Angebots- bzw. der Bedarfs-Strategie ist das Feststellen desjenigen Ortes mit dem meisten Angebot bzw. Bedarf auch ein wichtiger Teil der Strategie. In der Grafik-Bedingung wird also möglicherweise einem Ort, der betrachtet wird, in dessen mentaler Repräsentation auch das Attribut hat noch am meisten? zugeordnet; in der Matrix-Bedingung muß es dagegen erst wieder inferiert werden.
Insgesamt scheint es also so, als wäre die mentale Repräsentation der Aufgaben bei den Versuchspersonen der Grafik-Bedingung etwas reichhaltiger, da dort einige für die Lösung der Aufgaben relevante Attribute direkt aus der Bildschirm-Darstellung abgelesen werden können und somit automatisch für die mentale Repräsentation der Aufgaben zur Verfügung stehen.
Die hier aufgeführten Daten - insbesondere die Tatsache, daß die Lösungen mit zunehmender Übung kaum besser wurden und daß die Versuchspersonen Schwierigkeiten hatten, die angeblich angewandte Strategie zu nennen - legen es nahe, daß im Verlauf des Experiments kein Strategieerwerb stattfand.
Statt dessen wurde bei der Erzeugung der Lösung wahrscheinlich nur der jeweils nächste Schritt geplant und ausgeführt. Dieses schrittweise Vorwärts-Arbeiten (forward working) führt nach Sweller (1988) - wie oben dargestellt - zu einer Verringerung der Work-Load. Die sich jeweils ergebende neue Situation konnte dann direkt vom Bildschirm abgelesen werden und als Grundlage für die weitere Planung verwendet werden. Dadurch ergab sich der Vorteil, daß die auftretende Work-Load deutlich reduziert wurde, weil die Ergebnisse eines Schrittes nicht mental evaluiert und gespeichert werden mußten, sondern bei Bedarf direkt abgelesen werden konnten. Dies zeigte sich unter anderem in der Korrelation zwischen der Lösungszeit und der Anzahl der Schritte für die Lösung und darin, daß in der experimentellen graphischen Bedingung deutlich geringere Lösungszeiten benötigt wurden als in der experimentellen Matrix-Bedingung, in der die benötigten Informationen nicht so schnell und einfach encodiert werden konnten.
6. Erklärung des Verhaltens der Versuchspersonen
Eine saliente Beziehung zwischen der Eingabe des Benutzers und den beobachtbaren Reaktionen des Systems ist nach Berry und Broadbent (1988) - wie oben dargestellt - Voraussetzung dafür, daß die dem Verhalten eines Systems zugrundeliegenden Regeln gelernt werden können. In dem hier beschriebenem Experiment ist keine der drei von Berry und Broadbent (1988) genannten Voraussetzungen für eine solche saliente Beziehung erfüllt: Die absolute Höhe der einzelnen Kosten stellt einen irrelevanten Faktor dar, der die Versuchsperson z.B. dazu bringen kann, tatsächlich zu rechnen. Der Zusammenhang zwischen den einzelnen Aktionen und der Güte der Lösung ist nicht sehr deutlich, da die Versuchsperson erst am Ende der Bearbeitung einer Aufgabe darüber Rückmeldung erhält, wie gut diese gelöst wurde. Die Versuchspersonen wurden außerdem nicht instruiert, nach Regelhaftigkeiten oder Strategien zu suchen, sondern nur, eine möglichst günstige Lösung zu finden. Aus den genannten Gründen ist es deshalb wahrscheinlich, daß in diesem Experiment das Lernen gemäß dem unselektiven Modus erfolgte. Die verbalisierten Strategien konnten wohl teilweise deshalb nicht direkt in den Daten nachgewiesen werden, weil sie erst zum Zeitpunkt der Befragung rekonstruiert wurden.
Die wiederholte Bearbeitung der Aufgaben führte zwar nicht zum Erwerb einer globalen Lösungsstrategie, es wurden aber lokale Heuristiken erlernt, wie etwa das Beginnen mit der billigsten Verbindung oder das Vergeben von maximal vielen Einheiten. Diese Heuristiken wurden eher implizit gelernt, was sich vor allem daran zeigt, daß sie von den Versuchspersonen zwar angewandt, aber in der postexperimentellen Befragung nicht genannt wurden. Der Grund bestand, wie oben aufgeführt, zum einen in der nicht hinreichend salienten Beziehung zwischen den Aktionen der Versuchspersonen und ihren Auswirkungen und zum anderen in der Instruktion.
Die Tatsache, daß im Verlauf des Experiments die Lösungen in der experimentellen Bedingung zwar schneller gefunden wurde, aber nicht besser wurden, kann damit begründet werden, daß vor allem die Encodierung der Information und die Abarbeitung der Eingabe verbessert wurden. Dabei handelte es sich um den Erwerb von skills im Sinne von Rasmussen (1986). Der Erwerb von Regeln (rule-based behavior) beschränkte sich im Experiment wohl auf lokale Regeln, die angewandt werden konnten, ohne daß ein Gesamtplan zur Lösung der Aufgaben vorlag. Erlernen von Planungswissen (knowledge-based behavior) fand dagegen wahrscheinlich nur bei jenen Versuchspersonen statt, die die optimale Strategie als solche erkannten.
Nach Rasmussen (1986) sollte der Erwerb der verschiedenen Ebenen der Fertigkeiten in der entgegengesetzten Richtung, also vom knowledge-based zum skill-based behavior, erfolgen, so daß immer weniger bewußte Kontrolle erforderlich ist. Dazu ist es aber Voraussetzung, daß die Versuchspersonen von Anfang an mit der anzuwendenden Strategie vertraut sind; dies war nur bei den Kontrollgruppen der Fall.
Daß der Lernerwerb in den experimentellen Gruppen etwas deutlicher (der Unterschied war aber nicht signifikant) war als in den Kontroll-Gruppen, kann daran liegen, daß bei der Lösung der Aufgaben ohne bekannten Lösungsweg öfter Informationen vom Bildschirm abgelesen werden mußten und sich somit der Lernfortschritt dieser Komponente der Lösungsfindung deutlicher bemerkbar macht. Für das häufigere Ablesen von Informationen können zwei Gründe angeführt werden: Erstens gehen durch die höhere Belastung des Arbeitsgedächtnisses öfter Elemente daraus verloren und müssen deshalb neu abgelesen werden. Zweitens führt das Fehlen einer bestimmten Lösungsstrategie dazu, daß nicht genau bekannt ist, welche Informationseinheiten zur Lösung relevant sind; es müßte daher öfter vorkommen, daß Informationen encodiert werden, die sich als irrelevant herausstellen.
In der Kontroll-Gruppe wirkte sich dagegen das effizientere Encodieren der präsentierten Informationen nicht so deutlich auf die gesamte Lösungszeit aus, da dort nicht so oft Informationen encodiert wurden.
Um das Verhalten der Versuchspersonen in dem Experiment in den Konzepten von Andersonīs Theorie beschreiben zu können, müßte dieses Verhalten in Produktionen beschrieben werden. Erstens müssen Produktionen zum Encodieren der jeweils benötigten Informationen aus der Bildschirmrepräsentation vorhanden sein. Zweitens werden Produktionen zur Auswahl geeigneter Operatoren (also einzelner Schritte, die aus einer Verbindung und der Anzahl zu vergebender Einheiten bestehen) benötigt. Drittens braucht die Versuchsperson noch Produktionen zur Realisierung der ausgewählten Schritte, also zu deren Eingabe.
Der meiste Teil der zur Lösung der Aufgaben benötigten Informationen dürfte aus der Aufgabenstellung am Bildschirm abgelesen werden (siehe oben). Die zur Lösung neuartiger Probleme anfangs eingesetzten weak methods zur Verarbeitung des deklaratives Wissens dürften bei diesen Aufgaben vor allen in Vorwärts-Suche und eventuell auch Hill-Climbing (lokale Minimierung der Kosten) bestehen.
Gemäß den Instruktionen sollten die Versuchspersonen das Ziel verfolgen, möglichst niedrige Gesamtkosten zu verursachen. Daher werden sie in den Experimental-Gruppen von diesem Ziel aus (backward working) versucht haben, die Kosten der einzelnen Schritte möglichst niedrig zu halten. Daraus entstand möglicherweise das Ziel, zuerst auf der billigsten Verbindung Einheiten zu vergeben (was auch empirisch gesehen oft realisiert wurde). Von da an müßte vor allem Vorwärts-Suche (working forward) stattfinden: Nach Ausführung eines Schrittes wurde nur der nächste Schritt überlegt, da die begrenzte Kapazität des Arbeitsgedächtnis zusammen mit der Komplexität der Aufgaben eine weitgehendere Suche unmöglich macht. Darauf deutet auch die Korrelation zwischen der Anzahl der Schritte und der Zeit, die zur Lösung einer Aufgabe benötigt wurde, hin.
Der Ort, an dem gesuchte Werte stehen, braucht mit zunehmender Übung nicht jedesmal gesucht werden; mit etwas Übung im Umgang mit dem Interface bilden sich Produktionen, in denen der Ort, an dem bestimmte Informationen, die in ihnen benötigt werden, bereits "eingebaut" ist; die benötigte Information braucht also nicht erst gesucht zu werden. Umgekehrt erfolgt wohl auch ein Erlernen der Bedeutung der dargestellten Zahlen aufgrund ihrer Lokalisation am Bildschirm: Deren Beschriftung braucht nicht immer wieder codiert zu werden.
Bei den Experimental-Gruppen findet Composition für die Suche im Problemraum selbst wahrscheinlich selten statt, da ja (siehe oben) keine Erarbeitung einer "echten" Strategie erfolgt. Deshalb tritt auch keine feste Reihenfolge, in der die einzelnen Operatoren angewandt werden auf. Somit können auch kaum aufeinanderfolgende Schritte zusammengefaßt werden. Wenn eine Strategie, wie z.B. die optimale Strategie verfolgt wird, bei der zum Finden des nächsten Schrittes nur der vorherige Schritt und die Problemstellung bekannt sein müssen, können nur innerhalb eines Schrittes Produktionen kombiniert werden. Bei den Kontroll-Gruppen können deshalb kaum mehrere Schritte zusammengefaßt und auf einmal ausgeführt werden, weil für jeden einzelnen Schritt neue Informationen vom Bildschirm encodiert werden müssen.
Beim Encodieren von bestimmten Informationen lassen sich dagegen möglicherweise Produktionen zusammenfassen. Wenn z.B. bei einem Angebots- oder Bedarfs-Ort der Wert Null steht, braucht dieser Ort nicht weiter betrachtet zu werden; somit kann direkt auf die Feststellung, daß der Wert Null vorliegt, die Aktion erfolgen, die nächste Verbindung zu betrachten.
Da die Aufgaben sehr komplex sind, findet auch relativ wenig Lerngewinn statt (siehe oben); ein weiteres Indiz dafür, daß wenig gelernt wird, besteht darin, daß auch in der Kontrollgruppe noch relativ häufig Fehler bei der Anwendung der Strategie unterlaufen; dies deutet darauf hin, daß die Abarbeitung der Strategie nicht vollständig automatisiert wurde (möglicherweise waren es zu wenige Übungsdurchgänge).
Slips - Fehler bei der Ausführung bekannter Operatoren - treten bei der Abarbeitung verschiedener Strategien auf: In der Kontrollgruppe, in der die Versuchspersonen eigentlich genau wissen, was sie zu tun haben, wurden die angegebenen Regeln (die als Produktionen betrachtet werden können) nicht immer korrekt befolgt.
Der Fit der Mittelwerte der Lösungszeiten für die einzelnen Aufgaben im Verlauf des Experiments mittels eines power-law-Modells ist akzeptabel; auch der Fit mit einem exponentiellen Modell ist beinahe genauso gut. Nach den Ausführungen von Neves und Anderson (1981) sollte sich die Geschwindigkeit des Lernfortschritts zwischen den von diesen beiden Modellen vorhergesagten Werten bewegen.
Generalisierung/Diskrimination sind in diesem Zusammenhang nicht beurteilbar, da alle Aufgaben ähnlich sind und somit kein Transfer untersucht werden kann. Nach dem Konzept der Strength sollten häufig angewandte Produktionen noch schneller werden. Besonders häufig dürften Produktionen zum Ablesen von Informationen vom Bildschirm angewandt werden; es ist anzunehmen, daß ein großer Anteil der Abnahme der Lösungszeiten darauf zurückführbar ist.
7. Ausblick
Wenn die Eingabemechanismen bei beiden Bildschirmpräsentationen konstant gehalten werden und dennoch die bisher gefundenen Unterschiede in den Lösungszeiten zwischen den Bildschirmpräsentationen auftreten, dann kann dies als Bestätigung der Hypothese betrachtet werden, daß die unterschiedliche Bildschirmgestaltung und die daraus resultierenden Unterschiede in der kognitiven Belastung tatsächlich nur aufgrund der Encodierung der Informationen entstehen und nicht auf umständlichere oder weniger umständliche Eingabemechanismen zurückzuführen sind. Die Verwendung der selben Eingabemechanismen bei unterschiedlicher Bildschirmpräsentation ließe sich relativ einfach realisieren, indem die bei der graphischen Bedingung verwendeten Schieberegler nur noch zur Anzeige der eingestellten Werte verwendet werden; wenn sie durch Anklicken angewählt würden, sollte sich das selbe numerische Eingabefeld öffnen, das bisher schon in der Matrix-Bedingung Verwendung fand.
Eine andere interessante Erweiterung des Experimentes könnte in der Durchführung eines Transfer-Experiments bestehen: Dazu müßte die Hälfte der Versuchspersonen zuerst Aufgaben in der Grafik-Bedingung bearbeiten und anschließend in der Matrix-Bedingung; die andere Hälfte der Versuchspersonen müßte die Aufgaben in der umgekehrten Reihenfolge lösen. Wenn sich der Lernerwerb, wie hier dargelegt, tatsächlich vor allem auf die Encodierung der Aufgabenstellung und die Eingabe der Lösungsschritte beschränkt - wenn also wenig eigentlicher Strategieerwerb stattfindet, sollte bei unterschiedlichen Bildschirmpräsentationen und Eingabemechanismen nur wenig positiver Transfer auftreten.
Wie zu Anfang dargestellt wurde, handelt es sich bei den in diesem Experiment verwendeten Aufgaben um typische Planungsaufgaben. Die Ergebnisse der Untersuchung deuten allerdings darauf hin, daß tatsächlich nur wenig Planung stattfand:
Wegen der hohen Belastung des Arbeitsgedächtnisses durch die Vielzahl dargebotener Informationseinheiten dürfte es den Versuchspersonen kaum möglich gewesen sein, die Teillösung weiter als einen Schritt im voraus mental zu erzeugen. Deshalb bleibt ihnen kaum eine andere Möglichkeit, als zu versuchen, die Lösung mittels Vorwärtssuche zu erhalten. Es werden also keine Pläne im Sinne der eingangs dargestellten Definitionen erstellt; es findet höchstens eine iterative plan-and-act structure (Anderson, 1990) statt.
Wegen der hohen kognitiven Belastung und der daraus resultierenden überwiegenden Anwendung der Vorwärtssuche kommt es dazu, daß kaum Strategieerwerb stattfindet (siehe Diskussionsteil; Sweller, 1988). Sollte das Ziel eines möglichst erfolgreichen Strategieerwerbs erreicht werden, müßte also vor allem die Komplexität der Aufgaben reduziert werden. Dies ist bei Aufgaben vom dargestellten Typ nicht möglich.
Um den Versuchspersonen ein Erlernen der Strategien dennoch möglich zu machen, hätten sie instruiert werden müssen, nach einer Strategie zu suchen. Der dadurch ausgelöste explorative Umgang mit den Aufgaben hätte möglicherweise dazu geführt, daß die optimale Strategie öfter erkannt worden wäre. Wegen der Instruktion, die Aufgaben möglichst optimal zu lösen, verwendeten die Versuchspersonen von Anfang an zu viel Kapazität darauf, die einzelnen Schritte der Lösung zu optimieren, so daß nicht mehr auf die Vorgehensweise insgesamt geachtet werden konnte (siehe dazu Berry und Broadbent, 1988).
Schließlich ist nochmals zu betonen, daß ein ergonomisch gestalteter Bildschirm nicht automatisch auch zu einem besseren Erlernen der zugrundeliegenden Mechanismen führt als eine weniger ergonomisch gestaltete Oberfläche, wenn das ergonomisch gestaltete Interface den Benutzer dazu verleitet, einfach gedankenlos verschieden Aktionen auszuprobieren (siehe Svendsen, 1991).
Literaturanhang
Alterman, R. (1988). Adaptive Planning. Cognitive Science, 12, 393-421.
Anderson, J. R., Greeno, J. G., Kline, P. J. & Neves, D. M. (1981). Acquisition of Problem-Solving Skill. In Anderson, J. R. (Ed), Cognitive Skills and Their Acquisition, pp. 191- 230. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Anderson, J. R. (1987). Skill Acquistion: Compilation of Weak-Method Problem Solutions. Psychological Review, 94(2), 192-210.
Anderson, J. R. (1990). The Adaptive Character of Thought. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Anderson, J. R. (1993). Problem Solving and Learning. American Psychologist, 48(1), 35-44.
Ashcraft, M. H. (1992). Cognitive arithmetic: A review of data and theory. Cognition, 44, 75 - 106.
Beach, K. D. (1988). The Role of External Mnemonic Symbols in Acquiring an Occupation. In Gruneberg, M. M., Morris, P. E. & Sykes, R. N. (Eds), Practical Aspects of memory: Current Research and Issues. Vol. 1: Memory in Everyday Life, pp. 342-346. Chichester: Wiley & Sons.
Berry, D. C. & Broadbent, D. E. (1984). On the Relationship between Task Performance and Associated Verbalizable Knowledge. The Quarterly Journal of Experimental Psychology, 36A, 209-231.
Berry, D. C. & Broadbent, D. E. (1988). Interactive tasks and the implicit-explicit distinction. British Journal of Psychology, 79, 251-272.
Bortz, J. (1985). Lehrbuch der Statistik: für Sozialwissenschaftler, 2. Auflage. Berlin: Springer.
Brehmer, B. (1987). Development of Mental Models for Decision in Technological Systems. In Rasmussen, J., Duncan, K. & Leplat, J. (Eds), New Technology and Human Error, pp. 111-120. Chichester: Wiley & Sons.
Brown, J. S. & VanLehn, K. (1980). Repair Theory: A Generative Theory of Bugs in Procedural Skills. Cognitive Science, 4, 379 - 426.
Card, S. K., Moran, T. P. & Newell, A. (1983). The psychology of human-computer interaction. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Card, S. K., Moran, T. P. & Newell, A. (1990): The Keystroke-Level Model for User Performance Time with Interactive Systems. In Preece, J., Keller, L. & Stolk, H. (Eds), Human-computer interaction: selected readings: a reader, pp. 327-356. Hertfordshire: Pentice Hall International.
Carlson, R. A., Khoo, B. H., Yaure, R. G. & Schneider, W. (1990). Acquisition of a Problem-Solving Skill: Levels of Organization and Use of Working Memory. Journal of Experimental Psychology: General, 119(2), 193-214.
Carlson, R. A., Sullivan, M. A. & Schneider, W. (1989). Practice and Working Memory Effects in Building Procedural Skill. Journal of Experimental Psychology: Learning, Memory, and Cognition, 15(3), 517-526.
Carraher, T. N., Carraher, D. W. & Schliemann, A. D. (1985). Mathematics in the streets and in schools. British Journal of Developmental Psychology, 3, 21-29.
Chi, M. T. H., Feltovich, P. J. & Glaser, R. (1981). Categorization and Representation of Physics Problems by Experts and Novices. Cognitive Science, 5, 121-152.
Cohen, J. & Cohen, P. (1983). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. 2nd edition. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Colley, A. M. & Beech, J. R. (1989). Acquiring and performing cognitive skills. In Colley, A. M. & Beech, J. R. (Eds), Acquisition and performance of cognitive skills, pp. 1-16. Chichester: John Wiley & Sons.
Dehaene, S. (1989). The psychophysics of numerical comparison: A reexamination of apparently incompatible data. Perception & Psychophysics, 45 (6), 557 - 566.
Dehaene, S., Dupoux, E. & Mehler, J. (1990). Is Numerical Comparison Digital? Analogical and Symbolic Effects in Two-Digit Number Comparison. Journal of Experimental Psychology: Human Perception and Performance, 16(3), 626 - 641.
Dehaene, S. (1992). Varieties of numerical abilities. Cognition, 44, 1 - 42.
Dunker, K. (1935). Zur Psychologie des produktiven Denkens. Dritter Neudruck, 1974. Berlin, Heidelberg, New York: Springer.
Ericsson, K. A. & Simon, H. A. (1984). Protocol Analysis: Verbal Reports as Data. Cambridge, MA: MIT-Press.
Fikes, R. E., Hart, P. E. & Nilsson, N. J. (1972). Learning and Executing Generalized Robot Plans. Artificial Intelligence, 3, 251-288.
Fikes, R. E. & Nilsson, N. J. (1971). Strips: A new approach to the application of theorem proving to problem solving. Artificial Intelligence, 2, 189-208.
Funke, J. (1991). Solving Complex Problems: Exploration and Control of Complex Systems. In Sternberg, R. J. & Frensch, P. A. (Eds), Complex Problem Solving: Principles and Mechanisms, pp. 185-222. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Gilhooly, K. J. & Green, A. J. K. (1989). Learning problem-solving skills. In Colley, A. M. & Beech, J. R. (Eds), Acquisition and performance of cognitive skills, pp. 85-111. Chichester: John Wiley & Sons.
Georgeff, M. P. (1987). Planning. Annual Review of Computational Science, 2, 359-400.
Greeno, J. G. (1978). Natures of Problem-Solving Abilities. In Estes, W. K. (Ed), Handbook of Learning and Cognitive Processes. Volume 5: Human Information Processing, pp. 239-270. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Greeno, J. G. (1989a). A Perspective on Thinking. American Psychologist, 44(2), 134-141.
Greeno, J. G. (1989b). Situations, Mental Models, and Generative Knowledge. In Klahr, D. & Kotovsky, K. (Eds), Complex Information Processing. The Impact of Herbert A. Simon, pp. 285-318. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Greeno, J. G. (1991a). Mathematical Cognition: Accomplishments and Challenges in Research. In Hoffman, R. R. & Palermo, D. S. (Eds), Cognition and the Symbolic Processes: Applied and Ecological Perspectives, pp. 255 -279. Hildsdals, N.J.: Lawrence Erlbaum Associates.
Greeno, J. G. (1991b). A view of mathematical problem solving in school. In Smith, M. U. (Ed), Toward a Unified Theory of Problem Solving: Views from the Content Domains, pp. 69 - 98. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Hacker, W., Heisig, B., Hinton, J., Kodwa, S. T. & Wiesner, B. (1992). Planende Handlungsvorbereitung I - Grundlagen und Wirkungen. Beitrag auf dem 37. Kongreß der Deutschen Gesellschaft für Psychologie.
Hammond, K. J. (1990). Explaining and Repairing Plans That Fail. Artificial Intelligence, 45, 173-228.
Hayes, J. R. & Simon, H. A. (1977). Psychological Differences among Problem Isomorphs. In Castellan, N. J., Pisoni, D. B. & Potts, G. (Eds), Cognitive theory, pp. 21-41. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Hayes, N. A. & Broadbent, D. E. (1988). Two models of learning for interactive tasks. Cognition, 22, 249-275.
Hayes-Roth, B. & Hayes-Roth, F. (1979). A Cognitive Model of Planning. Cognitive Science, 3, 275-310.
Heisig, B., Ullrich, R., Nebe, C. & Hacker, W. (1992). Planende Handlungsvorbereitung II - Lebensbereichsspezifität und Eigenständigkeit des Konstruktes. Beitrag auf dem 37. Kongreß der Deutschen Gesellschaft für Psychologie.
Hertzberg, J. (1989). Planen: Einführung in die Planerstellungsmethoden der Künstlichen Intelligenz. Mannheim; Wien; Zürich: BI-Wiss.-Verl.
Hoc, J.-M. (1988). Cognitive Psychology of Planning. London: Academic Press.
Hussy, W. (1991). Komplexes Problemlösen und Verarbeitungskapazität. Sprache & Kognition, 10(4), 208-220.
Hutchins, E. L., Hollan, J. D. & Norman, D. A. (1986). Direct Manipulation Interfaces. In Norman, D. A. & Draper, S. W. (Eds), User Centered System Design: New Perspectives on Human-Computer Interaction, pp. 87-124. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Johnson-Laird, P. N. (1989). Mental Models. In Posner, M. I. (Ed), Foundations of Cognitive Science, pp. 469-499. Cambridge, MA: MIT-Press.
Kaplan, C. A. & Simon, H. A. (1990). In Search of Insight. Cognitive Psychology, 22, 374-419.
Keppel, G. (1982). Design and Analysis. 2nd Edition. Englewood Cliffs, N.J.: Prentice-Hall, Inc.
Kotovsky, K. & Fallside, D. (1989). Representation and Transfer in Problem Solving. In Klahr, D. & Kotovsky, K. (Eds), Complex Information Processing. The Impact of Herbert A. Simon, pp. 69-108. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Kotovsky, K. & Simon, H. A. (1990). What Makes Some Problems Really Hard: Explorations in the Problem Space of Difficulty. Cognitive Psychology, 22, 143-183.
Larkin, J. H. (1989). Display-Based Problem Solving. In Klahr, D. & Kotovsky, K. (Eds), Complex Information Processing. The Impact of Herbert A. Simon, pp. 319-341. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Larkin, J. H. & Simon, H. A. (1987). Why a Diagram is (Sometimes) Worth Ten Thousand Words. Cognitive Science, 11, 65-100.
Lave, J., Murtaugh, M. & De La Rocha, O. (1984). The dialectics of arithmetic in grocery shopping. In Rogoff, B. & Lave, J. (Eds), Everyday cognition: Its development in social context, pp. 67 - 94. Cambridge, MA: Harvard University Press.
Leplat, J. (1988). Task complexity in work situations. In Rasmussen, J., Goodstein, L. P., Olsen, S. E. & Andersen, H. B: (Eds), Tasks, errors and mental models: a festschrift to celebrate the 60th birthday of Professor Jens Rasmussen, pp. 105-115. London: Taylor & Francis Ltd.
Lewis, C. H. (1979). Speed and Practice. Unpublished Manuscript. [erwähnt in: Neves, D. M. & Anderson, J. R. (1981). Knowledge Compilation: Mechanisms for the Automatization of Cognitive Skills. In Anderson, J. R. (Ed), Cognitive Skills and Their Acquisition, pp. 57-84. Hillsdale, N.J.: Lawrence Erlbaum Associates.]
Mayer, R. E. (1982). Different problem solving strategies for word and equation problems. Journal of Experimental Psychology: Learning, Memory, and Cognition, 8(5), 448-462.
Mayer, R. E. & Gallini, J. K. (1990). When Is an Illustration Worth Ten Thousand Words? Journal of Educational Psychology, 82(4), 715-726.
Meshkati, N. (1988). Toward Development of a Cohesive Model of Workload. In Hancock, P. A. & Meshkati, N. (Eds), Human Mental Workload, pp. 305-314. North-Holland: Elsevier Science Publishers B.V.
Meshkati, N. & Loewenthal, A. (1988). The effects of individual differences in information processing behavior on experiencing mental workload and perceived task difficulty: A preliminary experimental investigation. In Hancock, P. A. & Meshkati, N. (Eds), Human Mental Workload, pp. 269-288. North-Holland: Elsevier Science Publishers B.V.
Nährer, W. (1982). Zur Beziehung zwischen Bearbeitungtsstrategie & Zeitbedarf bei Denkaufgaben. Zeitschrift für experimentelle und angewandte Psychologie, 29(1), 147-159.
Neves, D. M. & Anderson, J. R. (1981). Knowledge Compilation: Mechanisms for the Automatization of Cognitive Skills. In Anderson, J. R. (Ed), Cognitive Skills and Their Acquisition, pp. 57-84. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Newell, A. & Rosenbloom, P. S. (1981). Mechanisms of Skill Acquisition and the Law of Practice. In Anderson, J. R. (Ed), Cognitive Skills and Their Acquisition, pp. 1-55. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Norman, D. A. (1983). Some Observations on Mental Models. In Gentner, D. & Stevens, A. L. (Eds), Mental Models, pp. 7-14. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Norman; D. A. (1986). Cognitive Engineering. In Norman, D. A. & Draper, S. W. (Eds), User Centered System Design: New Perspectives on Human-Computer Interaction, pp. 31-61. Hillsdale, N.J.:Lawrence Erlbaum Associates.
Pfeiffer, T. (1991). Mentale Evaluation von Plänen. Regensburg: Dissertation.
Rasmussen, J. (1986). Information Processing and Human-Machine Interaction. New York: Elsevier Science Publishing Co.
Reimann, P. & Chi, M. T. H. (1989). Human Expertise. In Gilhooly, K. J. (Ed), Human and Machine Problem Solving, pp. 161-191. New York: Plenum-Press.
Rouse, W. B. & Morris, N. M. (1986). On Looking Into the Black Box: Prospects and Limits in the Search for Mental Models. Psychological Bulletin, 100(3), 349-363.
Sacerdoti, E. D. (1974). Planning in a Hierarchy of Abstraction Spaces. Artificial Intelligence, 5, 115-135.
Sanderson, P. M. (1989a). The Human Planning and Scheduling Role in Advanced Manufacturing Systems: An Emerging Human Factors Domain. Human Factors, 31(6), 635-666.
Sanderson, P. M. (1989b). Verbalizable Knowledge and Skilled Task Performance: Association, Dissociation, and Mental Models. Journal of Experimental Psychology: Learning, Memory, and Cognition, 15(4), 729-747.
Shneiderman, B. (1987). Designing the User Interface: Strategies for Effective Human-Computer Interaction. Reading, MA: Addison-Wesley.
Siegler, R. S. (1987). The Perils of Averaging Data Over Strategies: An Example From Childrenīs Addition. Journal of Experimental Psychology: General, 116(3), 250-264.
Simon, H. A. (1975). The Functional Equivalence of Problem Solving Skills. Cognitive Psychology, 7, 268-288.
Sokol, S. M. & McCloskey, M. (1991). Cognitive Mechanisms in Calculation. In Sternberg, R. J. & Frensch, P. A. (Eds), Complex Problem Solving: Principles and Mechanisms, pp. 85 - 116. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Stefik, M. J. (1981a). Planning with Constraints. Artificial Intelligence, 16(2), 111-140.
Stefik, M. J. (1981b). Planning and Meta-Planning. Artificial Intelligence, 16(2), 141-170.
Stevens, J. (1992). Applied multivariate statistics for the social sciences, 2nd edition. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Svendsen, G. B. (1991). The influence of interface style on problem solving. International Journal of Man-Machine Studies, 35, 379-397.
Sweller, J. (1988). Cognitive Load During Problem Solving: Effects on Learning. Cognitive Science, 12, 257-285.
Sweller, J., Chandler, P., Tierney, P. & Cooper, M. (1990). Cognitive Load as a Factor in the Structuring of Technical Material. Journal of Experimental Psychology: General, 119(2), 176-192.
VanLehn, K. (1989). Problem Solving and Cognitive Skill Acquisition. In Posner, M. I. (Ed), Foundations of Cognitive Science, pp. 527-579. Cambridge, MA.: MIT-Press.
VanLehn, K. (1991). Rule Acquisition Events in the Discovery of Problem-Solving Strategies. Cognitive Science, 15, 1-47.
Wickens, C. D. (1992). Engineering Psychology and Human Performance, Second Edition. New York: HarperCollins Publishers Inc.
Wiesner, B. (1992). Untersuchungen des individuellen Planungsverhaltens. Informationen der TU Dresden. 14-01-92. Dresden: TU-Eigenverlag.
Wilensky, R. (1983). Planning and Understanding. A Computational Approach to Human Reasoning. Reading, MA: Addison-Wesley.
Wilkins, D. E. (1984). Domain-independent Planning: Representation and Plan Generation. Artificial Intelligence, 22, 269-301.
Wilkins, D. E. (1988). Practical Planning: Extending the Classical AI Planning Paradigm. San Mateo, CA: Kaufmann.
Wöhe, G. (1981). Einführung in die Allgemeine Betriebswirtschaftslehre. 14., überarbeitete Auflage. München: Vahlen.
Wontorra, H. & Krems, J. (1989). Acquisition of strategies depending on the opponentīs competence level. Archiv für Psychologie, 141, 113-126.
Zimmermann, W. (1990). Operations Research: quantitative Methoden zur Entscheidungsvorbereitung. 5., überarbeitete Auflage. München; Wien: Oldenburg Verlag.
Anhang A: Der Bildschirm der Grafik-Bedingung
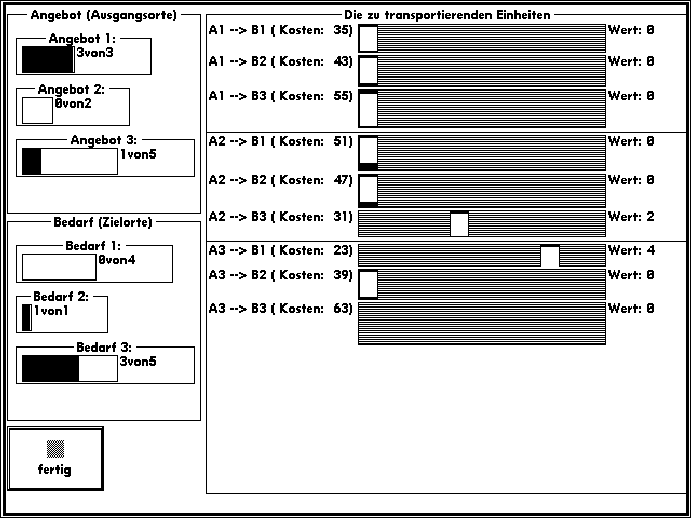
Anhang B: Der Bildschirm der Matrix-Bedingung
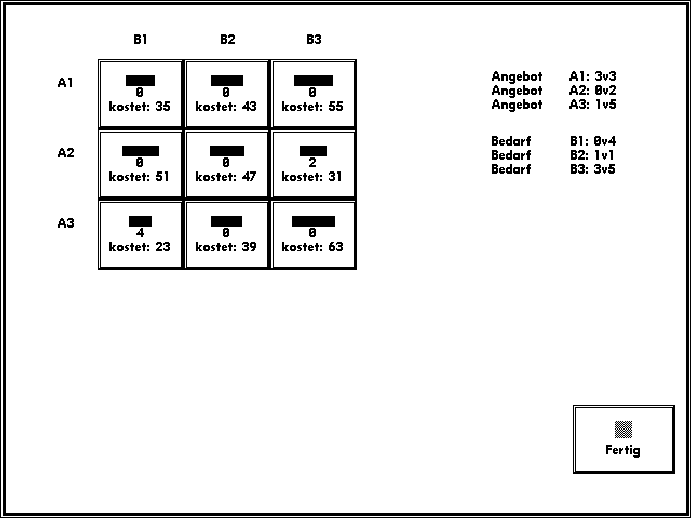
Anhang C: Die Instruktionen der Grafik-Bedingung:
Stellen Sie sich bitte folgendes Problem vor:
An den zwei Orten A1 und A2 stehen 10 bzw. 5 leere Eisenbahnwagen. In den Orten B1, B2 und B3 werden dagegen 3, 6 und 6 dieser Wagen benötigt. Diese Situation läßt sich tabellarisch folgendermaßen darstellen:
Angebot: Bedarf:
Ausgangsort A1: 10 Zielort B1: 3
Ausgangsort A2: 5 Zielort B2: 6
Zielort B3: 6
Die Entfernungen zwischen den einzelnen Orten bestimmt, wie teuer der Transport kommt; die Kosten lassen sich aus folgender Matrix ersehen:
Entfernung:
|
|
nach B1 nach B2 nach B3 |
|
von A1 von A2 |
kostet: 15 kostet: 17 kostet: 8 kostet: 20 kostet: 9 kostet: 31 |
Ihre Aufgabe ist es nun, festzulegen wie viele Wagen von jedem Ausgangsort in jeden Zielort transportiert werden sollen. Dabei müssen allerdings bestimmte Randbedingungen beachtet werden:
- Die Summe der von einem Ausgangsort wegtransportierten Wagen muß genau dem Angebot in diesem Ort entsprechen (es bleibt nichts übrig und es darf nicht mehr vergeben werden als vorhanden ist);
- Die Summe der an einem Zielort von den einzelnen Ausgangsorten "angelieferten" Wagen muß dem Bedarf an dem jeweiligen Ort entsprechen (es dürfen nicht zu viele oder zu wenige Wagen angeliefert werden).
Wird versucht, an einem Zielort mehr Wagen anzuliefern, als dort benötigt werden, oder wird versucht, von einem Ausgangsort aus mehr Wagen wegzutransportieren, als dort insgesamt vorhanden sind, wird der eingegebene Wert automatisch so verringert, daß nur die maximal mögliche Anzahl eingesetzt wird.
Ziel der Aufgabe ist es, eine Lösung zu finden, die insgesamt möglichst geringe Gesamtkosten ermöglicht, dabei aber gleichzeitig den oben genannten Randbedingungen genügt. Die Gesamtkosten ergeben sich aus der Summe der Kosten aller Strecken, die alle Wagen von den Ausgangsorten zu den jeweiligen Zielorten zurücklegen müssen. Sie berechnet sich also als die Summe aller Produkte aus Anzahl der zwischen zwei Orten transportierten Wagen und den Kosten dieser Strecken.
Für das hier vorgestellte Beispiel gibt es folgende optimale Lösung:
|
|
nach B1 nach B2 nach B3 |
|
von A1 von A2 |
3 1 6 0 5 0 |
In dem nun folgenden Experiment werden Ihnen die Informationen zur Ausgangssituation folgendermaßen am Bildschirm dargestellt: Links sehen Sie für jeden Ausgangsort bzw. Zielort einen Balken dargestellt, der angibt wieviel Angebot in diesem Ort noch vorhanden ist bzw. wieviel Bedarf in diesem Ort noch benötigt wird.
Auf der rechten Hälfte des Bildschirms sehen Sie eine Reihe von Schiebereglern, mit denen Sie angeben können, wieviele Einheiten von einem Ort zu einem anderen transportiert werden sollen. Die Eingabe eines Wertes erfolgt dadurch, daß mit der Maus auf den "Schieberegler" gezeigt wird, dann der linke Knopf gedrückt wird und dann der Regler in die gewünschte Position geschoben wird, während der linke Knopf gedrückt bleibt. Soll für eine Verbindung der Wert Null beibehalten werden, braucht dieser nicht extra angegeben zu werden.
Die einzelnen Aufgabe werden unterschiedlich komplex sein.
Viel Spaß!
Anhang D: Die Instruktionen der Matrix-Bedingung:
Stellen Sie sich bitte folgendes Problem vor:
An den zwei Orten A1 und A2 stehen 10 bzw. 5 leere Eisenbahnwagen. In den Orten B1, B2 und B3 werden dagegen 3, 6 und 6 dieser Wagen benötigt. Diese Situation läßt sich tabellarisch folgendermaßen darstellen:
Angebot: Bedarf:
Ausgangsort A1: 10 Zielort B1: 3
Ausgangsort A2: 5 Zielort B2: 6
Zielort B3: 6
Die Entfernungen zwischen den einzelnen Orten bestimmt, wie teuer der Transport kommt; die Kosten lassen sich aus folgender Matrix ersehen:
Entfernung:
|
|
nach B1 nach B2 nach B3 |
|
von A1 von A2 |
kostet: 15 kostet: 17 kostet: 8 kostet: 20 kostet: 9 kostet: 31 |
Ihre Aufgabe ist es nun, festzulegen wie viele Wagen von jedem Ausgangsort in jeden Zielort transportiert werden sollen. Dabei müssen allerdings bestimmte Randbedingungen beachtet werden:
- Die Summe der von einem Ausgangsort wegtransportierten Wagen muß genau dem Angebot in diesem Ort entsprechen (es bleibt nichts übrig und es darf nicht mehr vergeben werden als vorhanden ist);
- Die Summe der an einem Zielort von den einzelnen Ausgangsorten "angelieferten" Wagen muß dem Bedarf an dem jeweiligen Ort entsprechen (es dürfen nicht zu viele oder zu wenige Wagen angeliefert werden).
Wird versucht, an einem Zielort mehr Wagen anzuliefern, als dort benötigt werden, oder wird versucht, von einem Ausgangsort aus mehr Wagen wegzutransportieren, als dort insgesamt vorhanden sind, wird der eingegebene Wert automatisch so verringert, daß nur die maximal mögliche Anzahl eingesetzt wird.
Ziel der Aufgabe ist es, eine Lösung zu finden, die insgesamt möglichst geringe Gesamtkosten ermöglicht, dabei aber gleichzeitig den oben genannten Randbedingungen genügt. Die Gesamtkosten ergeben sich aus der Summe der Kosten aller Strecken, die alle Wagen von den Ausgangsorten zu den jeweiligen Zielorten zurücklegen müssen. Sie berechnet sich also als die Summe aller Produkte aus Anzahl der zwischen zwei Orten transportierten Wagen und den Kosten dieser Strecken.
Für das hier vorgestellte Beispiel gibt es folgende optimale Lösung:
|
|
nach B1 nach B2 nach B3 |
|
von A1 von A2 |
3 1 6 0 5 0 |
In dem nun folgenden Experiment werden Ihnen die Informationen zu den Kosten und die Anzahl der von Ihnen vergebenen Einheiten in einer Tabelle zusammengefaßt am Bildschirm dargestellt. Das Angebot in den einzelnen Ausgangsorten bzw. der Bedarf in den Zielorten werden auf der rechten Seite des Bildschirms angezeigt. Es ist Ihre Aufgabe, die einzelnen Felder der Tabelle durch Anklicken mit den Werten zu füllen, die zu einer möglichst optimalen Lösung führen. Anfänglich steht überall der Wert Null; soll dieser beibehalten werden, braucht er nicht nochmals extra eingegeben zu werden.
Die einzelnen Aufgabe werden unterschiedlich komplex sein.
Viel Spaß!
Anhang E: Die Erläuterung der optimalen Strategie
Die optimale Strategie
Die gestellten Aufgaben können alle mit folgender Strategie optimal gelöst werden:
Man sucht sich die Verbindung mit dem niedrigsten Kostenwert und vergibt auf dieser möglichst viele Einheiten. Möglichst viel heißt, entweder so viele, wie Angebot verfügbar ist, oder so viel, wie noch Bedarf am Zielort der Verbindung besteht; der kleinere der beiden Werte ist der maximal zu vergebende Wert. Dann sucht man die Verbindung mit den nächstniedrigen Kosten und vergibt auf dieser Strecke möglichst viel. Wenn auf einer Verbindung kein Angebot mehr vorhanden ist bzw. wenn kein Bedarf mehr besteht, dann geht man direkt zu der Verbindung mit den nächsthöheren Kosten. Auf diese Weise werden der Reihe nach alle Verbindungen abgearbeitet, bis kein Angebot bzw. Bedarf mehr vorhanden ist.
Manchmal bleiben zum Schluß "teuere" Verbindungen übrig, auf denen relativ viel transportiert werden muß; dadurch soll man sich nicht beirren lassen: Die genaue Befolgung der Strategie führt immer zur optimalen Lösung.
Anhang F: Die nach dem Experiment gestellten Fragen
1.) Versuche, Dich an alles zu erinnern, woran Du bei der Lösung der letzten Aufgabe gedacht hast. Was fällt Dir noch ein?
2.) Stell Dir vor, Du solltest einer anderen Person, die auch an diesem Experiment teilnehmen wird, dabei helfen. Welche Tips könntest Du ihr geben, damit sie schneller gute Lösungen findet?
3.) Wie sieht eine gute Lösung aus; woran erkennt man sie?
4.) Wie sieht eine schlechte Lösung aus; woran erkennt man sie?
5.) Welche Fehler hast Du gemacht oder welche Fehler könnte man machen?
6.) Aus welchen Einheiten (Objekten) besteht eine der gestellten Aufgaben?
7.) Nach welchen Merkmalen der Aufgabe hast Du Ausschau gehalten? Wonach hast Du zuerst gesucht?
8.) Sind Dir zwischen den einzelnen Aufgaben systematische Unterschiede aufgefallen? Gab es Klassen von Aufgaben?
8.a) Haben sich diese Klassen in ihrer Schwierigkeit unterschieden? Warum?
9.) Kannst Du allgemeine Regeln nennen, die zur Lösung der Aufgabe verwendet werden können? Welche?
Anhang G: Die Angebots-Strategie:
Bei dieser Strategie wird das temporäre höchste Angebot möglichst billig vergeben:
1. Suche das höchste temporäre Angebot X. Existieren zwei gleich billige Alternativen, wird diejenige gewählt, bei der ein billigerer Transport möglich ist.
2. Suche den Bedarfsort Y, zu dem dieses Angebot am billigsten transportiert werden kann
3. Transportiere möglichst viel von X nach Y.
4. Wenn noch Angebot vorhanden ist, gehe zu 1.
Anhang H: Die Bedarfs-Strategie:
Bei dieser Strategie wird der temporäre höchste Bedarf möglichst billig befriedigt:
1. Suche den höchsten temporären Bedarf Y. Existieren zwei gleich billige Alternativen, wird diejenige gewählt, bei der ein billigerer Transport möglich ist.
2. Suche den Angebotsort X, der diesen Bedarf am billigsten befriedigen kann.
3. Transportiere möglichst viel von X nach Y.
4. Wenn noch Bedarf vorhanden ist, gehe zu 1.
zurück zur Skriptenseite
zurück zu meiner homepage
rainer@zwisler.de