Einführung in die Matrixrechnung

Matrizen

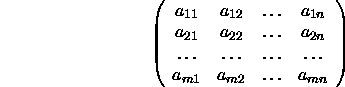
K sei ein beliebiger Zahlenkörper. Eine rechteckige Anordnung der Form

wird Matrix über K oder auch einfach Matrix genannt (wenn K implizit vorgegeben ist), wobei die Skalare in K sind. Die oben definierte Matrix wird gekennzeichnet durch die Schreibweise oder kurz durch .

Die m horizontalen n-Tupel

sind die Zeilen der Matrix (sie besitzt also m Zeilen mit je n Einträgen); die n vertikalen m-Tupel

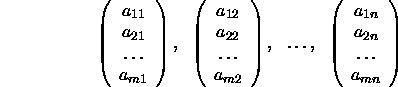
sind die Spalten der Matrix (sie besitzt also n Spalten mit je m Einträgen).

Das Element wird auch das ij-Element oder die ij-Komponente genannt; es erscheint in der i-ten Zeile und in der j-ten Spalte. Eine Matrix mit m Zeilen und n Spalten wird m mal n Matrix genannt, oder auch Matrix; das Zahlenpaar (m, n) wird als die Größe der Matrix bezeichnet.

Matrizen werden gewöhnlich durch die Großbuchstaben bezeichnet; die Elemente des Zahlenkörpers K, aus denen sie sich zusammensetzen, werden durch die Kleinbuchstaben bezeichnet.

DEFINITION: Zwei Matrizen A und B sind gleich, geschrieben A = B, wenn sie die gleiche Größe haben und wenn die korrespondierenden Elemente gleich sind. Demnach ist Gleichheit von zwei Matrizen äquivalent mit einem System von Gleichungen (jeweils eine Gleichung für jedes Paar korrespondierender Elemente).

ANMERKUNG: Eine Matrix mit einer Zeile wird Zeilenvektor genannt; eine Matrix mit nur einer Spalte nennt man Spaltenvektor. Insbesondere kann ein Element des Zahlenkörpers K auch als eine Matrix gesehen werden.

Matrixaddition

Zwei Matrizen lassen sich nur dann addieren, wenn sie die selbe Größe besitzen. Es seien also A und B zwei Matrizen mit gleicher Größe; beides seien Matrizen:

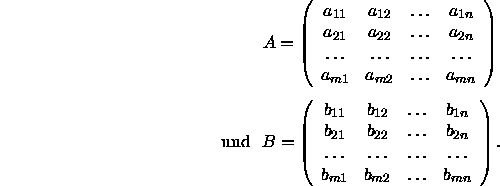
Die Summe von A und B, geschrieben A + B, ist diejenige Matrix, die man erhält, wenn man die korrespondierenden Elemente addiert:

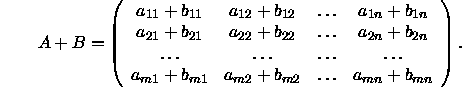
Die Summe von Matrizen unterschiedlicher Größe ist nicht definiert.

Skalare Multiplikation

Das Produkt einer Matrix A mit einem Skalar k, geschrieben oder einfach kA ist diejenige Matrix, die man erhält, wenn jedes Element der Matrix A mit k multipliziert wird:

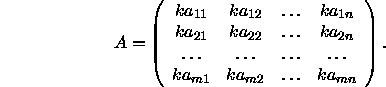
ANMERKUNG: Es ist zu beachten, daß A + B und kA wiederum Matrizen sind. Außerdem wird definiert:

(i)

(ii)

A - B = a + (-B)

Die Matrix, deren Elemente alle Null sind, also

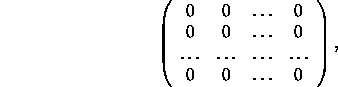
wird Nullmatrix genannt und wird gekennzeichnet durch 0. Sie ist dem Skalar 0 ähnlich, und zwar insofern, daß für eine beliebige Matrix gilt:

Für die Matrixaddition und für die skalare Multiplikation gelten die folgenden Rechenregeln: Es sei V die Menge aller Matrizen über dem Zahlenkörper K. Dann gilt für beliebige Matrizen und für beliebige Skalare :

(i)

(A + B) + C = A + (B + C)

(ii)

A + 0 = A

(iii)

A + (-A) = 0

(iv)

A + B = B + A

(v)

(vi)

(vii)

(viii)

und

Matrixmultiplikation

Wir gehen zunächst vom einfacheren Fall der Vektormultiplikation aus: Es wird angenommen, die Vektoren und sind Elemente des n-dimensionalen Raumes ; A werde durch einen Zeilenvektor und B durch einen Spaltenvektor repräsentiert. Dann läßt sich deren Vektorprodukt finden, indem man die Matrizen folgendermaßen kombiniert:

Für den allgemeineren Fall der Matrixmultiplikation geht man nun von einer Matrix A und einer Matrix B aus:

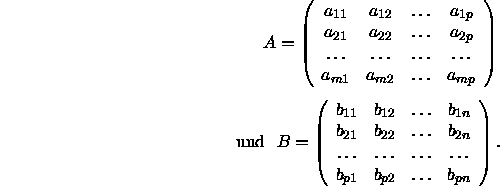
Definiert man als den i-ten Zeilenvektor von A und als den j-ten Spaltenvektor von B, so kann man auch schreiben:

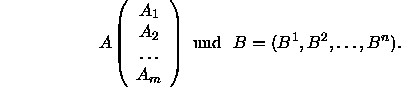
Dann erhält man als Produkt AB eine Matrix, deren ij-tes Element jeweils durch die Multiplikation der i-ten Zeile von A mit der j-ten Spalte von B zu erhalten ist:

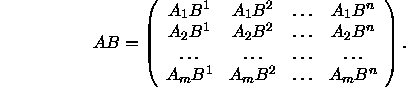
Hier sei nochmals das Produkt ausführlich hingeschrieben: AB =

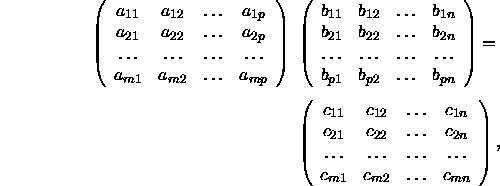
wobei gilt .

Es werden also immer Elemente aus Zeilen der ersten Matrix mit Elementen aus Spalten der zweiten Matrix multipliziert und dann wird aufsummiert. Um sich diese Vorgehensweise besser merken zu können, sollte man sich das Wort Zeitschriften einprägen: Zeilen werden mit Schpalten multipliziert.

WICHTIG: Es sei betont, daß das Produkt AB nicht definiert ist, wenn A eine Matrix und B eine Matrix ist, wobei gilt.

Die Matrixmultiplikation ist nicht komutativ ist, d.h. die Produkte AB und BA müssen nicht gleich sein. Für die Matrixmultiplikation müssen aber die folgenden Rechenregeln gelten:

(i)

(AB) C = A (B C) (Assoziativgesetz)

(ii)

A(B + C) = AB + AC (linkes Distributivgesetz)

(iii)

(B + C) A = BA + CA (rechtes Distributivgesetz)

(iv)

k(AB) = (kA)B = A(kB), wobei k ein Skalar ist.

(v)

0A = 0 und B0 = 0, wobei 0 die Nullmatrix ist.

Transponierte

Die Transponierte einer Matrix A, geschrieben , ist diejenige Matrix, die man erhält, wenn man die Zeilen von A als Spalten schreibt, und zwar folgendermaßen:

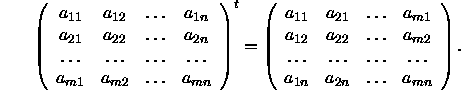
Dabei ist zu beachten, daß eine Matrix ist, wenn A eine Matrix ist.

BEISPIEL:

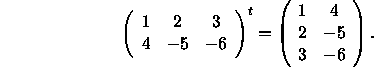
Das Transponieren von Matrizen unterliegt den folgenden Rechenregeln:

(i)

(ii)

(iii)

, wobei k ein Skalar ist

(iv)

Quadratische Matrizen

DEFINITION: Eine Matrix, die die gleiche Zahl an Zeilen und Spalten besitzt, heißt eine quadratische Matrix. Eine Matrix mit n Zeilen und n Spalten heißt eine Matrix der Ordnung n oder auch n-Quadrat-Matrix. Die Diagonale (oder auch Hauptdiagonale) der n-Quadrat-Matrix besteht aus den Elementen .

Eine obere Dreiecksmatrix ist eine quadratische Matrix, deren Elemente unterhalb der Hauptdiagonalen Null sind:

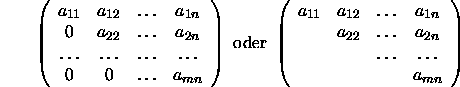
Eine untere Dreiecksmatrix ist eine quadratische Matrix, deren Elemente oberhalb der Hauptdiagonalen Null sind. Eine Diagonalmatrix ist eine quadratische Matrix, deren nichtdiagonale Elemente alle Null sind:

Eine besondere Matrix ist die n-Quadrat-Matrix mit Einsen auf der Hauptdiagonalen und überall sonst Nullen; sie wird mit oder einfach mit I bezeichnet. Diese Matrix heißt Einheitsmatrix; sie kann beispielsweise folgendermaßen aussehen:

Diese Matrix verhält sich bei Berechnungen ähnlich wie das Skalar 1: Es gilt für jede n-Quadrat-Matrix A:

Die Matrix kI heißt Skalarmatrix (wobei für den Skalar gelten muß); dabei handelt es sich um eine Diagonalmatrix, deren Diagonalelemente alle gleich k sind.

Determinanten

Jeder quadratischen Matrix kann man auf bestimmte Weise einen Skalar zuordnen, der die Determinante der Matrix genannt wird. Für die Determinante einer Matrix A schreibt man oder auch .

Die Determinante der n-quadratischen Matrix heißt von der Ordnung n und wird häufig bezeichnet mit

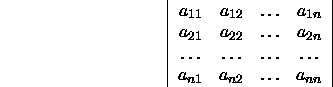
ACHTUNG: Eine quadratische Anordnung von skalaren Größen, dir von senkrechten Strichen eingeschlossen wird, ist nicht eine Matrix, sondern der Skalar, der der entsprechenden Matrix zugeordnet ist.

Man kann Determinanten beispielsweise zur Bestimmung des Ranges einer Matrix, zur Berechnung der Inversen einer Matrix und bei der Lösung linearer Gleichungssysteme benutzen; auch für die Theorie der Eigenwerte sind sie unentbehrlich. Zu ihrer Bestimmung ist allerdings ein enormer Rechenaufwand notwendig.

An dieser Stelle möchte ich jetzt nur die Formeln zur Berechnung der Determinanten von quadratischen Matrizen der Dimensionen 1 bis 3 vorstellen:

Die Determinante einer -Matrix ist der Skalar selbst:

Die Determinante einer -Matrix 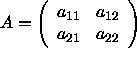berechnet sich nach der folgenden Formel:

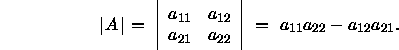
Die Determinante einer -Matrix berechnet sich nach der folgenden Formel:

Invertierbare Matrizen

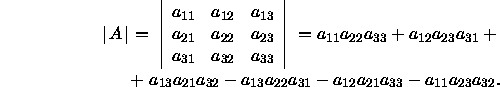
Wenn für eine gegebene Matrix A eine Matrix B derart existiert, daß AB = BA = I gilt, dann heißt B eine Inverse von A und wird mit bezeichnet.

Die Berechnung der Inversen ist relativ kompliziert; wir wollen sie hier nur für den Fall einer -Matrix 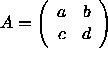betrachten: Wir suchen die Skalare x, y, z, w so, daß gilt:

oder

Diese Gleichung entspricht den beiden folgenden Systemen von linearen Gleichungen mit zwei Unbekannten:

Wenn man nun noch die Determinante definiert als

dann haben die oben dargestellten Gleichungen - wenn gilt - die folgenden eindeutigen Lösungen:

Somit gilt also:

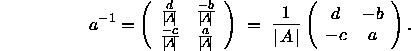
zurück zur Übungsseite (Farbwahrnehmung)
zurück zu meiner homepage

Anmerkungen und Mitteilungen an

Last modified 10-30-98